資料科學家成長指南(上)
少年,你渴望力量麼?
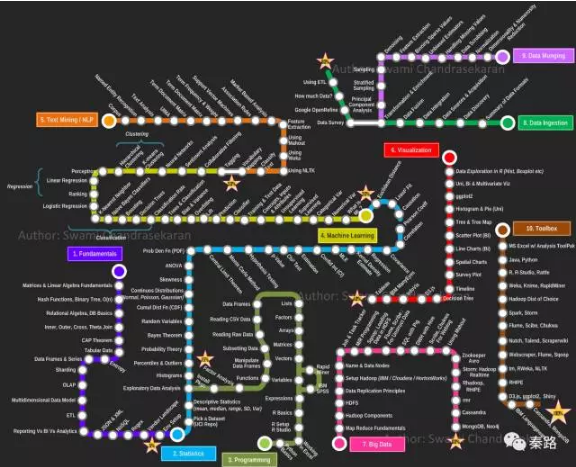
這才是真正的力量,年輕人!
這是Swami Chandrasekaran所繪製的一張地圖。名字叫MetroMap to Data Scientist(資料科學家之路),別稱怎麼死都不知道的。
資料科學家是近年火爆興起的職位,它是資料分析師的後續進階,融合了統計、業務、程式設計、機器學習、資料工程的複合型職位。
該地圖一共十條路線,分別是基礎原理、統計學、程式設計能力、機器學習、文字挖掘/自然語言處理、資料視覺化、大資料、資料獲取、資料清理、常用工具。條條路線都不是人走的。因為網上只有英文版,我將其翻譯成中文,並對內容作一些解釋和補充。
該指南主要涉及硬技能,資料科學家的另外一個核心業務能力,這裡沒有涉及,它並不代表不重要。
——————
Fundamentals原理
算是多學科的交叉基礎,屬於資料科學家的必備素質。
Matrices & Linear Algebra
矩陣和線性代數
矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合。涉及到的機器學習應用有SVD、PCA、最小二乘法、共軛梯度法等。
線性代數是研究向量、向量空間、線性變換等內容的數學分支。向量是線性代數最基本的內容。中學時,數學書告訴我們向量是空間(通常是二維的座標系)中的一個箭頭,它有方向和數值。在資料科學家眼中,向量是有序的數字列表。線性代數是圍繞向量加法和乘法展開的。
矩陣和線性代數有什麼關係呢?當向量進行線性變換時,這種變換可以想象成幾何意義上的線性擠壓和拉扯,而矩陣則是描述這種變換的資訊,由變換後的基向量決定。
矩陣和線性代數是一體的,矩陣是描述線性代數的引數。它們構成了機器學習的龐大基石。
Hash Functions,Binary Tree,O(n)
雜湊函式,二叉樹,時間複雜度
雜湊函式也叫雜湊函式,它能將任意的資料作為輸入,然後輸出固定長度的資料,這個資料 叫雜湊值也叫雜湊值,用h表示,此時h就輸入資料的指紋。
雜湊函式有一個基本特性,如果兩個雜湊值不相同,那麼它的輸入也肯定不相同。反過來,如果兩個雜湊值是相同的,那麼輸入值可能相同,也可能不相同,故無法通過雜湊值來判斷輸入。
雜湊函式常用在資料結構、密碼學中。
二叉樹是電腦科學的一個概念,它是一種樹形結構。在這個結構中,每個節點最多有兩個子樹(左子樹和右子樹),子樹次序不能顛倒。二叉樹又有多種形態。
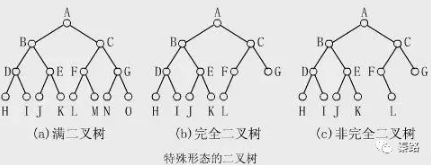
二叉樹是樹這類資料結構的第一種樹,後續還有紅黑樹等,很多語言的set,map都是用二叉樹寫的。
時間複雜度是程式設計中的一個概念,它描述了執行演算法需要的時間。不同演算法有不同的時間複雜度,例如快排、冒泡等。
簡便的計算方法是看有幾個for迴圈,一個是O(n),兩個是O(n^2),三個是O(n^3)。當複雜度是n^3+n^2時,則取最大的量級n^3即可。
與之相對應的還有空間複雜度,它代表的是算法佔用的記憶體空間。演算法通常要在時間和記憶體中取得一個平衡,既記憶體換時間,或者時間換記憶體。
Relational Algebra
關係代數
它是一種抽象的查詢語言。基本的代數運算有選擇、投影、集合並、集合差、笛卡爾積和更名。
關係型資料庫就是以關係代數為基礎。在SQL語言中都能找到關係代數相應的計算。
Inner、Outer、Cross、Theta Join
內連線、外連線、交叉連線、θ連線
這是關係模型中的概念,也是資料庫的查詢基礎。
內連線,只連線匹配的行,又叫等值連線。
外連線,連線左右兩表所有行,不論它們是否匹配。
交叉連線是對兩個資料集所有行進行笛卡爾積運算,比如一幅撲克牌,其中有A集,是13個牌的點數集合,集合B則是4個花色的集合,集合A和集合B的交叉連結就是4*13共52個。
θ連線使用where子句引入連線條件,θ連線可以視作交叉連線的一個特殊情況。where 可以是等值,也可以是非等值如大於小於。
不同資料庫的join方式會有差異。
CAP Theorem
CAP定理
指的是在一個分散式系統中, Consistency(一致性)、 Availability(可用性)、Partition tolerance(分割槽容錯性),三者不可得兼。
一致性(C):在分散式系統中的所有資料備份,在同一時刻是否同樣的值。(等同於所有節點訪問同一份最新的資料副本)
可用性(A):在叢集中一部分節點故障後,叢集整體是否還能響應客戶端的讀寫請求。(對資料更新具備高可用性)
分割槽容錯性(P):以實際效果而言,分割槽相當於對通訊的時限要求。系統如果不能在時限內達成資料一致性,就意味著發生了分割槽的情況,必須就當前操作在C和A之間做出選擇。
資料系統設計必須在三個效能方便做出取捨,不同的資料庫,CAP傾向性不同。
tabular data
列表資料
即二維的表格資料,關係型資料庫的基礎。
DataFrames & Series
Pandas資料結構
Series是一個一維資料物件,由一組NumPy的array和一組與之相關的索引組成。Python字典和陣列都能轉換成陣列。Series以0為開始,步長為1作為索引。
x = Series([1,2,3,4,5])
x
0 1
1 2
2 3
3 4
4 5
DataFrames是一個表格型的資料,是Series的多維表現。DataFrames即有行索引也有列索引,可以看作Series組成的字典。
Sharding
分片
分片不是一種特定的功能或者工具,而是技術細節上的抽象處理,是水平拓展的解決方法。一般資料庫遇到效能瓶頸,採用的是Scale Up,即向上增加效能的方法,但單個機器總有上限,於是水平拓展應運而生。
分片是從分割槽(Partition)的思想而來,分割槽通常針對表和索引,而分片可以跨域資料庫和物理假期。比如我們將中國劃分南北方,南方使用者放在一個伺服器上,北方使用者放在另一個伺服器上。
實際形式上,每一個分片都包含資料庫的一部分,可以是多個表的內容也可以是多個例項的內容。當需要查詢時,則去需要查詢內容所在的分片伺服器上查詢。它是叢集,但不同於Hadoop的MR。
如果能夠保證資料量很難超過現有資料庫伺服器的物理承載量,那麼只需利用MySQL5.1提供的分割槽(Partition)功能來改善資料庫效能即可;否則,還是考慮應用Sharding理念。另外一個流傳甚廣的觀點是:我們的資料也許沒有那麼大,Hadoop不是必需的,用sharding即可。
OLAP
聯機分析處理(Online Analytical Processing)
它是資料倉庫系統主要的應用,主要用於複雜的分析操作。
針對資料分析人員,資料是多維資料。查詢均是涉及到多表的複雜關聯查詢,為了支援資料業務系統的搭建,OLAP可以想象成一個多維度的立方體,以維度(Dimension)和度量(Measure)為基本概念。我們用到的多維分析就是OLAP的具象化應用。
OLAP更偏向於傳統企業,網際網路企業會靈活變動一些。另外還有一個OLTP的概念。
Multidimensional Data Model
多維資料模型。
它是OLAP處理生成後的資料立方體。它提供了最直觀觀察資料的方法。
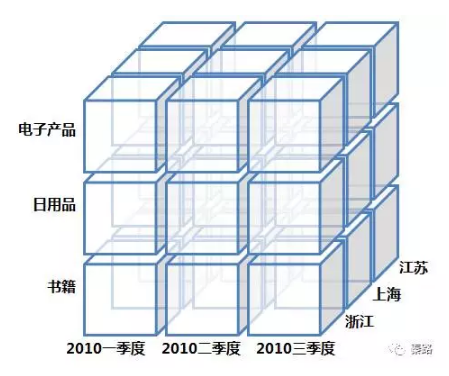
涉及鑽取,上卷,切片,切塊,旋轉等操作,就是把上面的立方體變變變啦。
ETL
ETL是抽取(extract)、轉換(transform)、載入(load)的過程。常用在資料倉庫。
整個流程是從資料來源抽取資料,結果資料清洗和轉換,最終將資料以特定模型載入到資料倉庫中去。
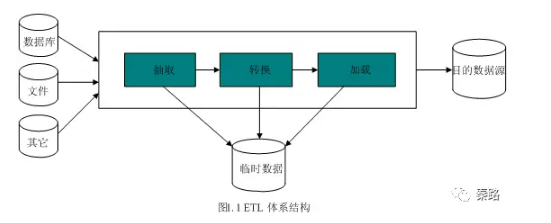
ETL是一個古老的概念,在以前SQL資料倉庫時代和OLAP伴隨而生,在現在日新月異的技術生態圈,會逐步演進到Hadoop相關的技術了。
Reporting vs BI vs Analytics
報表與商業智慧與分析
這是BI的三個組成部分。Reporting是資料報表。利用表格和圖表呈現資料。報表通常是動態多樣的。數個報表的集合統稱為Dashboard。
BI是商業智慧,是對企業的資料進行有效整合,通過資料報表快速作出決策。
Analytics是資料分析,基於資料報表作出分析。包括趨勢的波動,維度的對比等。
JSON & XML
JSON是一種輕量級的資料交換格式,易於閱讀和編寫,也易於機器解析和生成。
JSON的語法規則是:
-
{ }儲存物件;
-
[ ]儲存陣列;
-
資料由逗號分隔;
-
資料在鍵值對中;
下面範例就是一組JSON值
{
"firstName": "John",
"lastName": "Smith",
"age": 25,
"address": {
"streetAddress": "21 2nd Street",
"city": "New York",
"state": "NY",
"postalCode": "10021"
}
}
XML是可拓展標記語言,被設計用來傳輸和儲存資料,與之對應的HTML則是顯示資料。XML和HTML服務於不同目的,XML是不作為的。
<note>
<to>George</to>
<from>John</from>
<heading>Reminder</heading>
<body>Don't forget the meeting!</body>
</note>
上面的範例,純粹就是用來傳輸的一段資訊,沒有任何意義。
NoSQL
泛指非關係型的資料庫,意為Not Only SQL。
NoSQL是隨著大資料時代發展起來的,傳統的關係資料庫在高併發大規模多資料型別的環境下力不從心,而NoSQL就是為了解決這些問題而產生的。
NoSQL主要分為四大類:
鍵值KeyValue資料庫
這類資料庫會使用雜湊表,雜湊表中有一個特定的鍵指向一個特定的值,KeyValue的特點是去中心化,不涉及業務關係。代表Redis。
列資料庫
這類資料庫用於分散式海量儲存,和KeyValue的區別在於這裡的Key指向的是列。橫向拓展性好,適合大資料量高IO。代表HBase,Cassandra
文件型資料庫
屬於KeyValue資料庫的升級版,允許巢狀鍵值。文件是處理資訊的基本單位,一個文件等於一個關係資料庫的一條記錄。
因為文件的自由性,文件型資料庫適合複雜、鬆散、無結構或半結構化的資料模型,和JSON類似,叫做BSON(MongoDB的儲存格式)。代表MongoDB
圖形資料庫
基於圖論演算法的資料庫,將資料集以圖形元素(點、線、面)建立起來。這種資料庫常應用在社交網路關係鏈,N度關係等。代表Neo4j
Regex
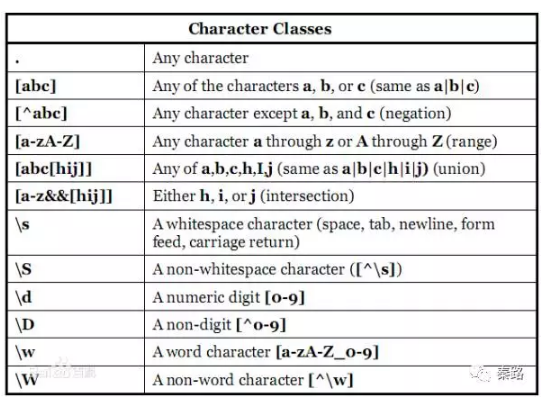
正則表示式(Regular Expression)
正則表通常被用來檢索、替換那些符合某個模式(規則)的字串。通過特定字元的組合,對字串進行邏輯過濾。例如註冊賬號時檢查對方郵件格式對不對啊,手機號格式對不對啊。
學起來靠記,記了也會忘,每次用得查,查了還得檢驗。網上記憶口訣一堆圖表,相關網站也不少,仁者見仁了。
Vendor Landscape
不懂,供應商風景?
Env Setup
環境安裝
想了半天,Env應該是環境安裝的意思,IDE啊,GUI啊等等全部安裝上去,再調各種路徑啥的。針對資料科學家,Anaconda + Rstudio用的比較多。
——————
Statistics 統計
統計是資料科學家的核心能力之一,機器學習就是基於統計學原理的,我不算精通這一塊,許多內容都是網路教科書式的語言。都掌握後再重寫一遍。
Pick a Dataset(UCI Repo)
找資料(UCI資料集)
UCI資料庫是加州大學歐文分校(University of CaliforniaIrvine)提出的用於機器學習的資料庫,這個資料庫目前共有335個數據集,其數目還在不斷增加,可以拿來玩機器學習。網上搜的到。另外的資料來源是Kaggle競賽等。
最經典的資料莫過於Iris了。
Descriptive Statistics(mean, median, range, SD, Var)
描述性統計(均值,中位數,極差,標準差,方差)
均值也叫平均數,是統計學中的概念。小學學習的算數平均數是其中的一種均值,除此以外還有眾數和中位數。
中位數可以避免極端值,在資料呈現偏態的情況下會使用。
極差就是最大值減最小值。
標準差,也叫做均方差。現實意義是表述各資料偏離真實值的情況,反映的是一組資料的離散程度。平均數相同的兩組資料,如[1,9]和[4,6],平均數相同,標準差不一樣,前者的離散程度更大。
方差,是標準差的平方。方差和標準差的量綱是一致的。在實際使用過程中,標準差需要比方差多一步開平方的運算,但它在描述現實意義上更貼切,各有優劣。
Exploratory Data Analysis
探索性資料分析
獲得一組資料集時,通常分析師需要掌握資料的大體情況,此時就要用到探索性資料分析。
主要是兩類:
-
圖形法,通過直方圖、箱線圖、莖葉圖、散點圖快速彙總描述資料。
-
數值法:觀察資料的分佈形態,包括中位數、極值、均值等,觀察多變數之間的關係。
探索性資料分析不會涉及到複雜運算,而是通過簡單的方式對資料有一個大概的瞭解,然後才去深入挖掘資料價值,在Python和R中,都有相關的summary函式。
Histograms
直方圖
它又稱質量分佈圖,是一種表示資料分佈的統計報告圖。
近似圖表中的條形圖,不過直方圖的條形是連續排列,沒有間隔、因為分組資料具有連續性,不能放開。
正常的直方圖是中間高、兩邊低、左右近似對稱。而異常型的直方圖種類過多,不同的異常代表不同的可能情況。
Percentiles & Outliers
百分位數和極值
它們是描述性統計的元素。
百分位數指將一組資料從小到大排序,並計算相遇的累積百分值,某一百分位所對應資料的值就稱為這一百分位的百分位數。比如1~100的陣列中,25代表25分位,60代表60分位。
我們常將百分位數均勻四等分:第25百分位數,叫做第一四分位數;第50百分位數,稱第二四分位數,也叫中位數;第75百分位數,叫做第三四分位數。通過四分位數能夠簡單快速的衡量一組資料的分佈。它們構成了箱線圖的指標。
極值是最大值和最小值,也是第一百分位數和第一百百分位數。
百分位數和極值可以用來描繪箱線圖。
Probability Theory
概率論,統計學的核心之一,主要研究隨機現象發生的可能性。
Bayes Theorem
貝葉斯定理
它關於隨機事件A和B的條件概率的定理。
現實世界有很多通過某些資訊推斷出其他資訊的推理和決策,比如看到天暗了、蜻蜓低飛了,那麼就表示有可能下雨。這組關係被稱為條件概率:用P(A|B)表示在B發生的情況下A發生的可能性。
貝葉斯公式:P(B|A) = P(A|B)*P(B) / P(A)
現實生活中最經典的例子就是疾病檢測,如果某種疾病的發病率為千分之一。現在有一種試紙,它在患者得病的情況下,有99%的準確判斷患者得病,在患者沒有得病的情況下,有5%的可能誤判患者得病。現在試紙說一個患者得了病,那麼患者真的得病的概率是多少?
從我們的直覺看,是不是患者得病的概率很大,有80%?90%?實際上,患者得病的概率只有1.9%。關鍵在哪裡?一個是疾病的發病率過低,一個是5%的誤判率太高,導致大多數沒有得病的人被誤判。這就是貝葉斯定理的作用,用數學,而不是直覺做判斷。
最經典的應用莫過於垃圾郵件的過濾。
Random Variables
隨機變數
表示隨機試驗各種結果的實際值。比如天氣下雨的降水量,比如某一時間段商城的客流量。
隨機變數是規律的反應,扔一枚硬幣,既有可能正面、也有可能反面,兩者的概率都是50%。扔骰子,結果是1~6之間的任何一個,概率也是六分之一。雖然做一次試驗,結果肯定是不確定性的,但是概率是一定的。隨機變數是概率的基石。
Cumul Dist Fn(CDF)
累計分佈函式(Cumulative Distribution Function)
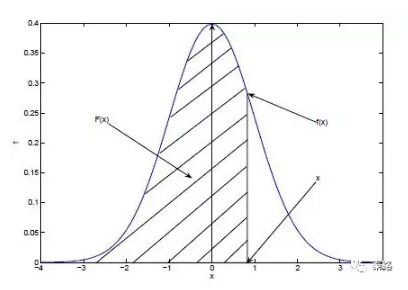
它是概率密度函式的積分,能夠完整描述一個實數隨機變數X的概率分佈。直觀看,累積分佈函式是概率密度函式曲線下的面積。
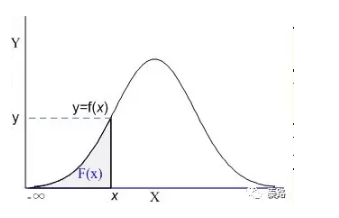
上圖陰影部分就是一個標準的累積分佈函式F(x),給定任意值x,計算小於x的概率為多大。實際工作中不會涉及CDF的計算,都是計算機負責的。記得在我大學考試,也是專門查表的。
現實生活中,我們描述的很多概率都是累積分佈函式,我們說考試90分以上的概率有95%,實際是90分~100分所有的概率求和為95%。
Continuos Distributions(Normal, Poisson, Gaussian)
連續分佈(正態、泊松、高斯)
分佈有兩種,離散分佈和連續分佈。連續分佈是隨機變數在區間內能夠取任意數值。
正態分佈是統計學中最重要的分佈之一,它的形狀呈鍾型,兩頭低,中間高,左右對稱。
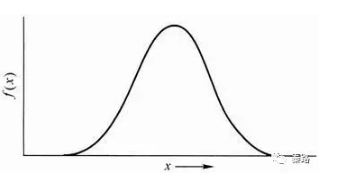
正態分佈有兩個引數,期望μ和標準差σ:μ反應了正態分佈的集中趨勢位置,σ反應了離散程度,σ越大,曲線越扁平,σ越小,曲線越窄高。
自然屆中大量的現象都按正態形式分佈,標準正態分佈則是正態分佈的一種,平均數為0,標準差為1。應用中,都會將正態分佈先轉換成標準正態分佈進行計算。很多統計學方法,都會要求資料符合正態分佈才能計算。
泊松分佈是離散概率分佈。適合描述某個隨機事件在單位時間/距離/面積等出現的次數。當n出現的次數足夠多時,泊松分佈可以看作正態分佈。
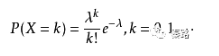
高斯分佈就是正態分佈。
Skewness
偏度
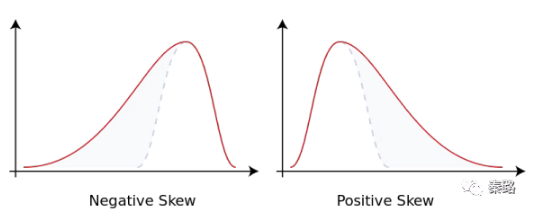
它是資料分佈傾斜方向和程度的度量,當資料非對稱時,需要用到偏度。
正態分佈的偏度為0,當偏度為負時,資料分佈往左偏離,叫做負偏離,也稱左偏態。反之叫右偏態。
ANOVA
方差分析
用於多個變數的顯著性檢驗。基本思想是:通過分析研究不同來源的變異對總變異的貢獻大小,從而確定可控因素對研究結果影響力的大小。
方差分析屬於迴歸分析的特例。方差分析用於檢驗所有變數的顯著性,而回歸分析通常針對單個變數的。
Prob Den Fn(PDF)
概率密度函式
PDF是用來描述連續型隨機變數的輸出值。概率密度函式應該和分佈函式一起看:
藍色曲線是概率密度函式,陰影部分是累積分佈函式。我們用概率密度函式在某一區間上的積分來刻畫隨機變數落在這個區間中的概率。概率等於區間乘概率密度,累積分佈等於所有概率的累加。
概率密度函式:f(x) = P(X=x)
累積分佈函式:F(x) = P(X<=x)
概率密度函式是累積分佈函式的導數,現有分佈函式,才有密度函式。累積分佈函式即可以離散也可以連續,而密度函式是用在連續分佈中的。
Central Limit THeorem
中心極限定理
它是概率論中最重要的一類定理。
自然屆中很多隨機變數都服從正態分佈,中心極限定理就是理解和解釋這些隨機變數的。我們有一個總體樣本,從中取樣本量為n的樣本,這個樣本有一個均值,當我們重複取了m次時,對應有m個均值,如果我們把資料分佈畫出來,得到的結果近似正態分佈。
這就是中心極限定理,它神奇的地方就在於不管總體是什麼分佈。我們很多推導都是基於中心極限定理的。
Monte Carlo Method
蒙特卡羅方法
它是使用隨機數來解決計算問題的方法。
蒙特卡羅是一個大賭場,以它命名,含義近似於隨機。我們有時候會因為各種限制而無法使用確定性的方法,此時我們只能隨機模擬,用通過概率實驗所求的概率來估計我們感興趣的一個量。最知名的例子有布豐投針試驗。
18世紀,布豐提出以下問題:設我們有一個以平行且等距木紋鋪成的地板,木紋間距為a,現在隨意拋一支長度l比木紋之間距離a小的針,求針和其中一條木紋相交的概率。布豐計算出來了概率為p = 2l/πa。
為了計算圓周率,人們紛紛投針,以實際的試驗結果來計算。
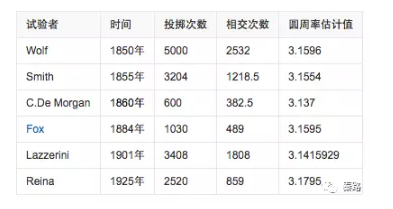
下圖則是計算機模擬的結果
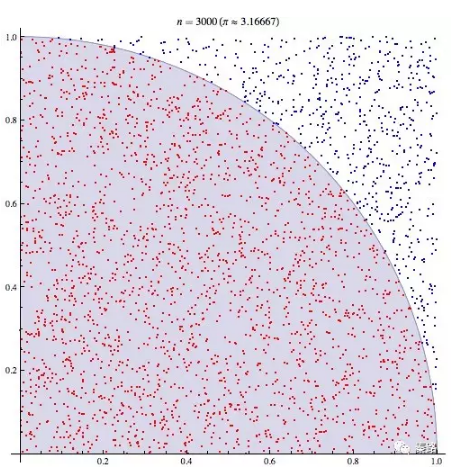
這就是蒙特卡羅方法的實際應用。它的理論依據是大數定理和中心極限定理。
Hypothesis Testing
假設檢驗
它是根據一定的假設條件由樣本推斷總體的方法。
首先根據實際問題作出一個假設,記作H0,相反的假設稱為備擇假設。它的核心思想是小概率反證法,如果這個假設發生的概率太小以至於不可能發生,結果它發生了,那麼我們認為假設是不成立的。
假設檢驗是需要容忍的,因為樣本會存在波動,這個波動範圍不會太嚴格,在這個範圍內出現的事件我們都能接受。但是我們都這麼容忍了,還是出現了違背原假設的小概率事件,那麼說明原假設有問題。不能容忍的範圍即拒絕域,在拒絕域發生的概率我們都認為它是小概率事件。
假設檢驗容易犯兩類錯誤,第一類錯誤是真實情況為h0成立,但判斷h0不成立,犯了“以真為假”的錯誤。第二類錯誤是h0實際不成立,但判斷它成立,犯了“以假為真”的錯誤。
假設檢驗有U檢驗、T檢驗、F檢驗等方法。
p-Value
P值
它是進行假設檢驗判定的一個引數。當原假設為真時樣本觀察結果(或更極端結果)出現的概率。P值很小,說明原假設發生的概率很小,但它確實發生了,那麼我們就有理由拒絕原假設。
至於P值的選擇根據具體情況,一般是1%,5%幾個檔次。
然而,P值在統計學上爭議很大,P值是否是接受原假設的標準,都是統計學各種流派混合後的觀點。P值從來沒有被證明可以用來接收某個假設(所以我上文的說明並不嚴謹),它只是僅供參考。現在統計學家們也開始倡導:應該給出置信區間和統計功效,實際的行動判讀還是留給人吧。
Chi2 Test
卡方檢驗
Chi讀作卡。通常用作獨立性檢驗和擬合優度檢驗。
卡方檢驗基於卡方分佈。檢驗的假設是觀察頻數與期望頻數沒有差別。
獨立性檢驗:卡方分佈的一個重要應用是基於樣本資料判斷兩個變數的獨立性。獨立性檢驗使用列聯表格式,因此也被稱為列聯表檢驗。原假設中,列變數與行變數獨立,通過每個單元格的期望頻數檢驗統計量。
擬合優度檢驗:它依據總體分佈狀況,計算出分類變數中各類別的期望頻數,與分佈的觀察頻數進行對比,判斷期望頻數與觀察頻數是否有顯著差異。目的是判斷假設的概率分佈模型是否能用作研究總體的模型。
獨立性檢驗是擬合優度檢驗的推廣。
Estimation
估計
統計學裡面估計分為引數估計和非引數估計。
引數估計是用樣本指標估計總體指標,這個指標可以是期望、方差、相關係數等,指標的正式名稱就是引數。當估計的是這些引數的值時,叫做點估計。當估計的是一個區間,即總體指標在某範圍內的可能時,叫做區間估計,簡單認為是人們常說的有多少把握保證某值在某個範圍內。
引數估計需要先明確對樣本的分佈形態與模型的具體形式做假設。常見的估計方法有極大似然估計法、最小二乘法、貝葉斯估計法等。
非引數估計則是不做假設,直接利用樣本資料去做逼近,找出相應的模型。
Confid Int(CI)
置信區間
它是引數檢驗中對某個樣本的總體引數的區間估計。它描述的是這個引數有一定概率落在測量結果的範圍程度。這個概率叫做置信水平。
以網上例子來說,如果在一次大選中某人的支援率為55%,而置信水平0.95以上的置信區間是(50%,60%),那麼他的真實支援率有95%的概率落在和50~60的支援率之間。我們也可以很容易的推得,當置信區間越大,置信水平也一定越大,落在40~70%支援率的可能性就有99.99%了。當然,越大的置信區間,它在現實的決策價值也越低。
置信區間經常見於抽樣調研,AB測試等。
MLE
極大似然估計
它是建立在極大似然原理的基礎上。
如果試驗如有若干個可能的結果A,B,C…。若在僅僅作一次試驗中,結果A出現,則一般認為試驗條件對A出現有利,也即A出現的概率很大。
此時我們需要找出某個引數,引數能使這個樣本出現的概率最大,我們當然不會再去選擇其他小概率的樣本,所以乾脆就把這個引數作為估計的真實值。
Kernel Density Estimate
核密度估計
它是概率論中估計未知的密度函式,屬於非引數檢驗。
一般的概率問題,我們都會假定資料分佈滿足狀態,是基於假定的判別。這種叫引數檢驗。如果如果資料與假定存在很大的差異,那麼這些方法就不好用,於是便有了非引數檢驗。核密度估計就是非引數檢驗,它不需要假定資料滿足那種分佈。
Regression
迴歸
迴歸,指研究一組隨機變數(Y1 ,Y2 ,…,Yi)和另一組(X1,X2,…,Xk)變數之間關係的統計分析方法,又稱多重回歸分析。通常Y1,Y2,…,Yi是因變數,X1、X2,…,Xk是自變數。
迴歸分析常用來探討變數之間的關係,在有限情況下,也能推斷相關性和因果性。而在機器學習領域中,它被用來預測,也能用來篩選特徵。
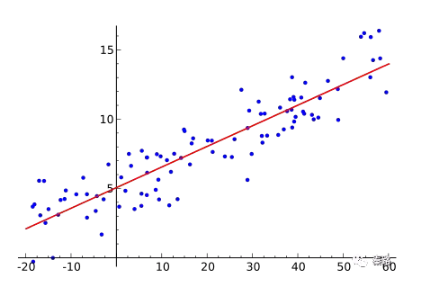
迴歸包括線性迴歸、非線性迴歸、邏輯迴歸等。上圖就是線性迴歸。
Convariance
協方差
用於衡量兩個變數的總體誤差,方差是協方差的一種特殊情況,即兩個變數相同。
協方差用資料期望值E計算:cov(x,y) = E[XY]-E[X][Y]。
如果XY互相獨立,則cov(x,y)=0.此時E[XY] = E[X][Y]。
Correlation
相關性
即變數之間的關聯性,相關性只涉及數學層面,即一個變數變化,另外一個變數會不會變化,但是兩個變數的因果性不做研究。
相關關係是一種非確定性的關係,即無法通過一個變數精確地確定另外一個變數,比如我們都認為,一個人身高越高體重越重,但是不能真的通過身高去確定人的體重。
Pearson Coeff
皮爾遜相關係數
它是度量兩個變數線性相關的係數,用r表示,其值介於-1與1之間。1表示完全正相關,0表示完全無關,-1表示完全負相關。
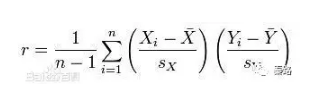
Causation
因果性
和相關性是一堆好基友。相關性代表數學上的關係,但並不代表具有因果性。
夏天,吃冷飲的人數和淹死的人數都呈現正相關。難道是吃冷飲導致了淹死?不是的,是因為天熱,天熱吃冷飲的人多了,游泳的人也多了。
《大資料時代》曾經強調,我們應該重視相關性而不是因果性,這是存疑的,因為對資料科學家來說,對業務因果性的瞭解往往勝於相關性,比如你預測一個人是否會得癌症,你不能拿是否做過放療作為特徵,因為放療已經是癌症的果,必然是非常強相關,但是對預測沒有任何幫助,只是測試資料上好看而已。
Least2 fit
最小二乘法
它是線性迴歸的一種用於機器學習中的優化技術。
最小二乘的基本思想是:最優擬合直線應該是使各點到迴歸直線的距離和最小的直線,即平方和最小。它是基於歐式距離的。
Eculidean Distance
歐氏距離
指在m維空間中兩個點之間的真實距離。小學時求的座標軸軸上兩個點的直線距離就是二維空間的歐式距離。很多演算法都是基於歐式距離求解的。
二維:
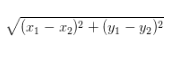
——————
Programming 程式設計
資料科學家是需要一定的程式設計能力,雖然不需要程式設計師那麼精通,注重的是解決的能力,而不是工程化的能力。作者從內容看更推崇R,我個人是推崇Python的。
Python Basics
Python基礎知識。
人生苦短,我用Python。
Python的基礎內容比R豐富的多,近幾年,Python有作為第一資料科學語言的趨勢。基礎內容就不多複述了。
Working in Excel
Excel幹活
掌握常用函式,懂得資料分析庫,會Power系列加分。VBA這種就不用學了。
R Setup, RStudio R
安裝R和RStudio
R是一門統計學語言。下列的內容,都是R語言相關。
R Basics
R的基礎,不多作陳述了。
Varibles
變數
變數是計算機語言中的抽象概念,可以理解成我們計算的結果或者值,不同計算語言的變數性質不一樣。主要理解R和Python的變數就行。大資料那塊可能還會涉及到Java和Scala。
R 用 <- 給變數賦值,=也能用,但不建議。
Vectors
向量
向量是一維陣列,可以儲存數值型、字元型或邏輯型資料的一維陣列。R裡面使用函式c( )建立向量。
v <- c(1,2,3,4)
向量中的資料必須擁有相同的資料型別,無法混雜。
Matrices
矩陣
矩陣是一個二維陣列,和向量一樣,每個元素必須擁有相同的資料型別。當維度超過2時,我們更建議使用陣列
m <- matrix(1:20,nrow=5,ncol=4)
Arrays
陣列
陣列與矩陣類似,但是維度可以大於2,資料型別必須一樣。
a <- array(1:20,c(4,5))
Factors
因子
因子是R中的有序變數和類別變數。
類別變數也叫做名義變數,它沒有順序之分,比如男女,雖然編碼中可能男為1,女為2,但不具備數值計算含義。有序變數則表示一種順序關係,少年、青年、老年則是一種有序變數。
f <- factor(c("type1","type2","type1))
在factor函式中加入引數ordered = True,就表示為有序型變量了。
Lists
列表
它是R最複雜的資料型別,它可以是上述資料結構的組合。
l <- list(names = v,m,a,f )
上述例子就包含了向量、矩陣、陣列、因子。我們可以使用雙重方括號[[ ]]選取列表中的元素。R中的下標不從0開始,所以list[[1]] 選取的是v。
Data Frames
資料框
在R和Python中為常用的資料結構。
R語言中為data.frame,Python中為Pandas的DataFrame。這裡以R語言舉例。
資料框可以包含不同資料型別的列,它是比矩陣更廣泛的概念,也是R中最常用的資料結構。每一列的資料型別必須唯一。
x <- data.frame(col1,col2,col3)
Reading CSV Data
讀取CSV
這一塊比較坑的地方是中文,R語言對中文編碼的支援比較麻煩。
Reading Raw Data
讀取原始資料
不清楚這和CSV的區別。
Subsetting Data
構建資料集
R提供了常用函式方便我們構建資料集(反正來去都那幾個英文)。
-
資料集合並使用merge函式。
-
新增資料行使用rbind函式。
-
dataframe選取子集用[ row,column]。
-
刪除變數可以通過 <- Null。
-
複雜查詢則使用subset函式。
-
如果已經習慣SQL函式,可以載入library(sqldf)後用sqldf函式。
Manipulate Data Frames
操作資料框
除了上面的構建資料集的技巧,如果我們需要更復雜的操作,加工某些資料,如求變數和、計算方差等,則要用到R語言的其他函式。
R本身提供了abs(x),sort(x),mean(x),cos(x)等常用的統計方法,如何應用在資料框呢?我們使用apply函式,可將任意一個函式應用在矩陣、陣列、資料框中。
apply(dataframe,margin,fun)
Functions
函式
R語言自帶了豐富的統計函式,可以通過官方/第三方文件查詢,R也可以自建函式。
myfunction <- function(arg1,arg2,……){
statements
return(object)
}
函式中的物件只在函式內部使用。如果要除錯函式,可以使用warning( ),messagr( ),stop( )等糾錯。
Factor Analysis
因子分析
我不知道這塊的程式設計基礎內容為什麼要加入因子分析。R語言的因子分析函式是factanal()
Install Pkgs
調包俠
R的包非常豐富(Python更是),可以通過cran下載,包括爬蟲、解析、各專業領域等。函式library可以顯示有哪些包,可能直接加入包。RStudio則提供了與包相關的豐富查詢介面。
——————
Machine Learning機器學習
資料科學的終極應用,現在已經是深度學習了。這條路也叫從調包到科學調參。這裡的演算法屬於經典演算法,但是向GBDT、XGBoost、RF等近幾年競賽中大發異彩的演算法沒有涉及,應該是寫得比較早的原因。
What is ML?
機器學習是啥子喲
機器學習,區別於資料探勘,機器學習的演算法基於統計學和概率論,根據已有資料不斷自動學習找到最優解。資料探勘能包含機器學習的演算法,但是協同過濾,關聯規則不是機器學習,在機器學習的教程上看不到,但是在資料探勘書本能看到。
Numerical Var
數值變數
機器學習中主要是兩類變數,數值變數和分量變數。
數值變數具有計算意義,可用加減乘除。資料型別有int、float等。
在很多模型中,連續性的數值變數不會直接使用,為了模型的泛化能力會將其轉換為分類變數。
Categorical Var
分類變數
分類變數可以用非數值表示,它是離散變數。
有時候為了方便和節省儲存空間,也會用數值表示,比如1代表男,0代表女。但它們沒有計算意義。在輸入模型的過程中,會將其轉變為啞變數。
Supervised Learning
監督學習
機器學習主要分為監督學習和非監督學習。
監督學習是從給定的訓練集中學習出一個超級函式Y=F(X),我們也稱之為模型。當新資料放入到模型的時候,它能輸出我們需要的結果達到分類或者預測的目的。結果Y叫做目標,X叫做特徵。當有新資料進入,能夠產生新的準確的結果。
既然從訓練集中生成模型,那麼訓練集的結果Y應該是已知的,知道輸入X和輸出Y,模型才會建立,這個過程叫做監督學習。如果輸出值是離散的,是分類,如果輸出值是連續的,是預測。
監督學習常見於KNN、線性迴歸、樸素貝葉斯、隨機森林等。
Unsupervied Learning
非監督學習
無監督學習和監督學習,監督學習是知道結果Y,無監督學習是不知道Y,僅通過已有的X,來找出隱藏的結構。
無監督學習常見於聚類、隱馬爾可夫模型等。
Concepts, Inputs & Attributes
概念、輸入和特徵
機器學習包括輸入空間、輸出空間、和特徵空間三類。特徵選擇的目的是篩選出結果有影響的資料。
Traning & Test Data
訓練集和測試集
機器學習的模型是構建在資料集上的,我們會採用隨機抽樣或者分層抽樣的將資料分成大小兩個部分,拿出大部分樣本進行建模型,留小部分樣本用剛建立的模型進行預報,通過小樣本的預測結果和真實結果做對比,來判斷模型優劣。這個叫做交叉驗證。
交叉驗證能夠提高模型的穩定性,但不是完全保險的,依舊有過擬合的風險。
通常用80%的資料構建訓練集,20%的資料構建測試集
Classifier
分類
監督學習中,如果輸出是離散變數,演算法稱為分類。
輸出的離散變數如果是二元的,則是二元分類,比如判斷是不是垃圾郵件{是,否},很多分類問題都是二元分類。與之相對的是多元分類。
Prediction
預測
監督學習中,如果輸出是連續變數,演算法稱為預測。
預測即可以是數值型,比如未來的銷量,也可以是介於[0,1]間的概率問題。
有些演算法適合分類、有些則是預測,也有演算法可以兩者都能做到。
Lift
Lift曲線
它是衡量模型效能的一種最常用的度量,它考慮的是模型的準確性。它核心的思想是以結果作導向,用了模型得到的正類數量比不用模型的效果提升了多少?
比如某一次活動營銷,1000個使用者會有200個響應,響應率是20%。用了模型後,我通過演算法,講使用者分群,挑出了最有可能響應的使用者200個,測試後的結果是有100個,此時的響應率變成了50%。此時的Lift值為5。
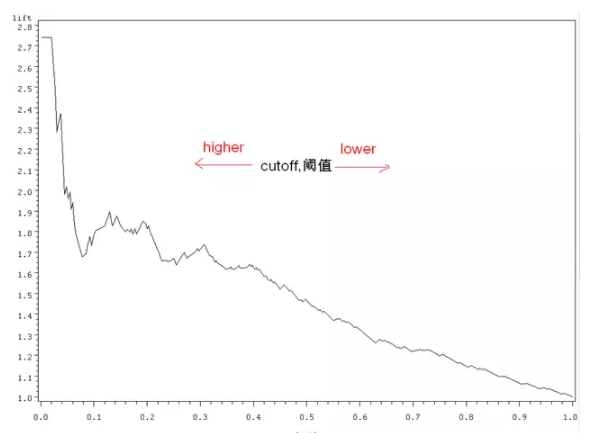
上圖就是按Lift值畫出曲線的範例。縱座標是lift值,橫座標是挑選的的閥值。閥值越低,說明挑選的越嚴格,按上文的例子理解,挑選的就是最有可能響應的使用者。當沒有閥值時,lift就為0了。閥值通常是根據預測分數排序的。
還有一種常用的叫ROC曲線。
Overfitting
過擬合
過擬合是機器學習中常碰到的一類問題。主要體現在模型在訓練資料集上變現優秀,而在真實資料集上表現欠佳。造成的原因是為了在訓練集上獲得出色的表現,使得模型的構造如此精細複雜,規則如此嚴格,以至於任何與樣本資料稍有不同的文件它全都認為不屬於這個類別。

上圖,黑色的線條是正常模型,綠色的線條是過擬合模型。
不同的機器學習演算法,是否容易擬合的程度也不僅相同。通常採用加大樣本資料量、減少共線性、增加特徵泛化能力的方法解決過擬合。
與之相反的是欠擬合。
Bias & Variance
偏差和方差
偏差和方差除了統計學概念外,它們也是解釋演算法泛化能力的一種重要工具。
演算法在不同訓練集上得到的結果不同,我們用偏差度量演算法的期望預測和真實結果的偏離程度,這代表演算法本身的擬合能力,方差則度量了演算法受資料波動造成的影響。
偏差越小、越能夠擬合數據,方差越小、越能夠扛資料波動。
Trees & Classification
樹分類
樹分類是需要通過多級判別才能確定模式所屬類別的一種分類方法。多級判別過程可以用樹狀結構表示,所以稱為樹分類器。最經典的便是決策樹演算法。
Classification Rate
分類正確率
為了驗證模型的好壞,即最終判斷結果的對錯,我們引入了分類正確率。
分類正確率即可以判斷二分類任務,也適用於多分類任務。我們定義分類錯誤的樣本數佔總樣本的比率為錯誤率,精確度則是正確的樣本數比率。兩者相加為1。
為了更好的判斷模型,主要是業務需要,我們還加入了查準率(precision),查全率(recall),查準率是預測為真的資料中有多少是真的。查全率是真的資料中有多少資料被預測對了。
這個有點繞,主要是為了業務判斷,假如我們的預測是病人是否患了某個致死疾病,假設得病為真,我們顯然希望把全部都得病的患者找出來,那麼此時查全率(得病的患者有多少被準確預測出來)比查準率(預測得病的患者有多少真的得病了)更重要,因為這個會死人,那麼肯定是選擇有殺錯無放過。此時更追求查全率。
演算法競賽就是基於上述指標評分的。
Decision Tress
決策樹
它是基本的分類和迴歸方法。可以理解成If-Then的規則集,每一條路徑都互斥且完備。決策樹分為內部節點和葉節點,內部節點就是If-Then的規則,葉節點就是分類結果。
決策樹主流有ID3、C4.5(C5.0也有了)、CART演算法。
因為決策樹形成的結構是根據樹形遞迴產生,它對訓練資料表現良好,但是會產生過擬合現象。為了避免這一現象,會進行減枝。剪紙通過損失函式或代價函式實現。
決策樹的優點是:高校簡單、可解釋性強、在大型資料庫有良好表現、適合高維資料。
缺點是:容易過擬合、並且分類結果會傾向擁有更多數值的特徵(基於資訊增益)。
隨機森林演算法是基於決策樹的。
Boosting
提升方法
屬於整合學習的一種。提升方法Boosting一般是通過多個弱分類器組成一個強分類器,提高分類效能。簡而言之是三個臭皮匠頂一個諸葛亮。
通過對訓練集訓練出一個基學習器,然後根據基學習器的分類表現跳轉和優化,分類錯誤的樣本將會獲得更多關注,以此重複迭代,最終產生的多個基分類器進行加強結合得出一個強分類器。
主流方法是AdaBoost,以基分類器做線性組合,每一輪提高前幾輪被錯誤分類的權值。
Naive Bayes Classifiers
樸素貝葉斯分類
它基於貝葉斯定理的分類方法。樸素貝葉斯法的使用條件是各條件互相獨立。這裡引入經典的貝葉斯定理:
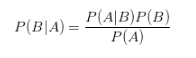
在演算法中,我們的B就是分類結果Target,A就是特徵。意思是在特徵已經發生的情況下,發生B的概率是多少?
概率估計方法有極大似然估計和貝葉斯估計,極大似然估計容易產生概率值為0的情況。
優點是對缺失資料不太敏感,演算法也比較簡單。缺點是條件互相獨立在實際工作中不太成立。
K-Nearest Neighbour
K近鄰分類。
K近鄰分類的特點是通過訓練資料對特徵向量空間進行劃分。當有新的資料輸入時,尋找距離它最近的K個例項,如果K個例項多數屬於某類,那麼就把新資料也算作某類。
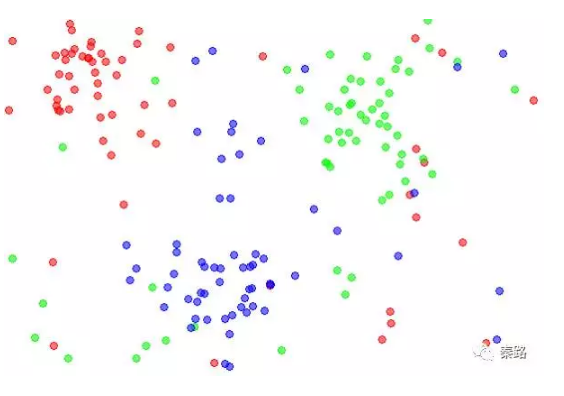
特徵空間中,每個訓練資料都是一個點,距離該點比其他點更近的所有點將組成一個子空間,叫做單元Cell,這時候,每個點都屬於一個單元,單元將是點的分類。
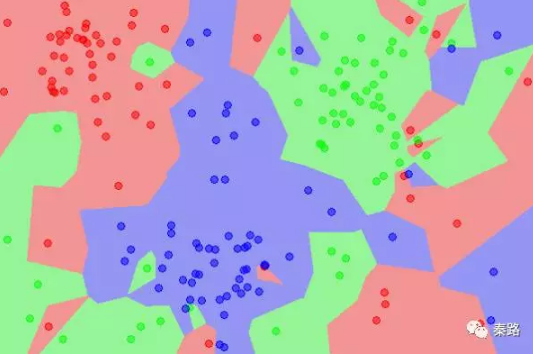
k值的選擇將會影響分類結果,k值越小,模型越複雜,容易過擬合,不抗干擾。K值越大,模型將越簡單,分類的準確度會下降。上圖是K=1時的子空間劃分,下圖是K=5時的子空間劃分,從顏色很直觀的看到影響。
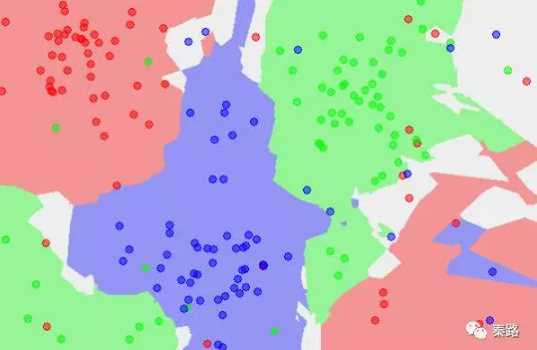
K近鄰的這類基於距離的演算法,訓練的時間複雜度低,為O(n),適用範圍範圍廣。但是時間複雜度低是通過空間複雜度換來的,所以需要大量的計算資源和記憶體。另外樣本不平衡問題解決不了。
Logistic Regression
邏輯斯諦迴歸,簡稱邏輯迴歸。
邏輯迴歸屬於對數線性模型,雖然叫回歸,本質卻是分類模型。如果我們要用線性模型做分類任務,則找到sigmoid函式將分類目標Y和迴歸的預測值聯絡起來,當預測值大於0,判斷正例,小於0為反例,等於0任意判別,這個方法叫邏輯迴歸模型。
模型引數通過極大似然法求得。邏輯迴歸的優點是快速和簡單,缺點是高維資料支援不好,容易錢擬合。
Ranking
排序,PageRank
這裡應該泛指Google的PageRank演算法。
PageRank的核心思想有2點:
-
如果一個網頁被很多其他網頁連結到的話說明這個網頁比較重要,也就是pagerank值會相對較高;
-
如果一個pagerank值很高的網頁連結到一個其他的網頁,那麼被連結到的網頁的pagerank值會相應地因此而提高。
PageRank並不是唯一的排名演算法,而是最為廣泛使用的一種。其他演算法還有:Hilltop 演算法、ExpertRank、HITS、TrustRank。
Linear Regression
線性迴歸
線性迴歸是機器學習的入門級別演算法,它通過學習得到一個線性組合來進行預測。
一般寫成F(x) = wx +b,我們通過均方誤差獲得w和b,均方誤差是基於歐式距離的求解,就是最小二乘法啦。找到一條線,所有資料到這條線的歐式距離之和最小。
線性迴歸容易優化,模型簡單,缺點是不支援非線性。
Perceptron
感知機
它是二類分類的線性分類模型。
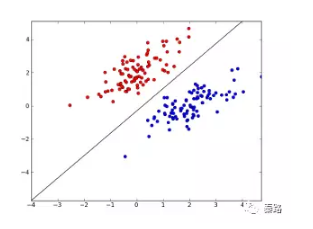
它通過一個wx+b的超平面S劃分特徵空間。為了找出這個超平面,我們利用損失函式極小化求出。超平面的解不是唯一的,採取不同初值或誤分類點將會造成不同結果。
Hierarchical Clustering
層次聚類
層次聚類指在不同層次對資料集進行劃分,從而形成樹形的聚類結構。
它將樣本看作一個初始聚類簇,每次運算找出最近的簇進行合併,該過程不斷合併,直到滿足預設的簇的個數。

上圖就是所有樣本重複執行最終K=1時的結果。橫軸是聚類簇之間的距離,當距離=5時,我們有兩個聚類簇,當距離=3時,我們有四個聚類簇。
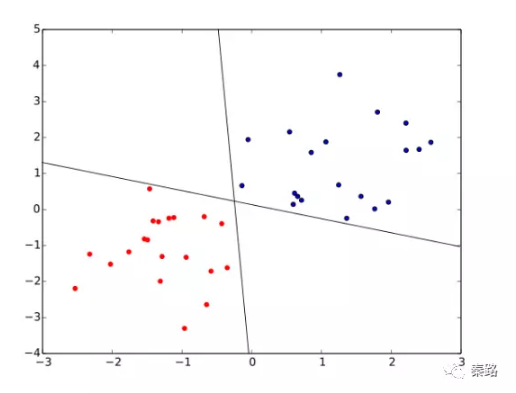
K-means Clusterning
K聚類
全稱K均值聚類,無監督學習的經典演算法。物以類聚人以群分的典型代表。
K聚類需要將原始資料無量綱化,然後設定聚類點迭代求解。K聚類的核心是針對劃分出的群簇使其最小化平方誤差。直觀說,就是讓樣本緊密圍繞群簇均值。
設定多少個聚類點多少有點主觀的意思,這也是K聚類唯一的引數,考察的是外部指標,即你聚類本身是想分出幾類,通過對結果的觀察以及E值判斷。
K聚類不適合多維特徵,一般3~4維即可,維度太多會缺乏解釋性,RFM模型是其經典應用。因為物以類聚,所以對偏離均值點的異常值非常敏感。
Neural Networks
神經網路
神經網路是一種模仿生物神經系統的演算法,神經網路演算法以神經元作為最基礎的單位,神經元通過將輸入資料轉換為0或1的閥值,達到啟用與否的目的,但是0和1不連續不光滑,對於連續性資料,往往用sigmoid函式轉換成[0,1] 間的範圍。
將這些神經單元以層次結構連線起來,就成了神經網路。因為這個特性,神經網路有許多的引數,可不具備可解釋性。多層神經網路,它的輸入層和輸出層之間的層級叫做隱層,就是天曉得它代表什麼含義。
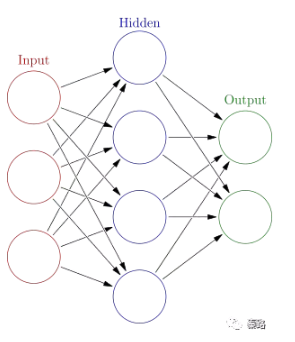
神經網路的層數一般是固定的,但我們也能將網路層數作為學習的目標之一,找到最適合的層數。
另外,層數越多,引數越多的神經網路複雜度越高,深度學習就是典型的層數很多的神經網路。常見的有CNN、DNN、RNN等演算法。
Sentiment Analysis
情感分析
比較前沿的一個領域。包括情感詞的正面負面分類,標註語料,情感詞的提取等。
情感分析可以通過情感關鍵詞庫計算,比如彙總開心、悲傷、難過的詞彙,計算情感值,再加入表示情感強烈程度的維度,如1~5的數值進行打分。使用者對商品評論的分析就是一個常見的情感分析:這手機太TM破了,就是5分憤怒。
然而情感詞典需要維護,構建成本較高,我們也可以用機器學習的方法將其看待為分類問題。講關鍵詞特徵向量化,常用詞袋模型(bag-of-words )以及連續分佈詞向量模型(word Embedding),特徵化後,往往用CNN、RNN或者SVM演算法。
Collaborative Fitering
協同過濾
簡稱CF演算法。協同過濾不屬於機器學習領域,所以你在機器學習的書上看不到,它屬於資料探勘。
協同過濾的核心是一種社會工程的思想:人們更傾向於向口味比較類似的朋友那裡獲得推薦。協同過濾主要分為兩類,基於使用者的user-based CF以及基於物體的item-based CF。雖然協同過濾不是機器學習,但它也會用到SVD矩陣分解計算相似性。
優點是簡單,你並不需要基於內容做內容分析和打標籤,推薦有新穎性,可以發掘使用者的潛在興趣點。
協同過濾的缺點是無法解決冷啟動問題,新使用者沒行為資料,也沒有好友關係,你是最不到推薦的;推薦會收到稀疏性的約束,你的行為越多,才會越準;隨著資料量的增大,演算法會收到效能的約束,並且難以拓展。
協同過濾可以和其他演算法混合,來提高效果。這也是推薦系統的主流做法。
Tagging
標籤/標註
這裡稍微有歧義、如果是標籤,間接理解為使用者畫像,涉及到標籤系統。使用者的男女、性別、出生地皆是標籤,越豐富的標籤,越能在特徵工程中為我們所用。
如果是分類標籤/標註,則是資料標註。有監督學習需要訓練集有明確的結果Y,很多資料集需要人工新增上結果。比如影象識別,你需要標註影象屬於什麼分類,是貓是狗、是男是女等。在語音識別,則需要標註它對應的中文含義,如果涉及到方言,則還需要將方言標註為普通話。
資料標註是個苦力活。
——————
個人水平一般,內容解讀不算好,可能部分內容有錯誤,歡迎指正。
因為微信文章最多2W字,所以該指南需要拆分成三篇。本文寫的是基礎原理、統計學、程式設計能力和機器學習。請大家期待後續。

