1005: [HNOI2008]明明的煩惱[prufer序列+組合數學]
阿新 • • 發佈:2018-11-07
題意:有一個n個點的無根樹,已經知道了它每個點的度數(也有可能沒有限制),詢問有多少種形式的無根樹滿足上述條件。
前置技能:
prufer序列
定義
任何一個無根樹都可以由一個
序列來唯一表示,其中度為
的節點在序列中出現
次。
構造
序列:
首先選擇節點序號最小的葉子節點,然後將與它相連的節點加入序列,然後把它自己刪掉,直到樹剩下只有兩個節點為止。
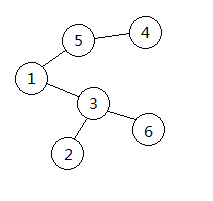
如上圖所以我們求他的prufer序列:
- 選擇最小的葉子節點 然後將與它相連的點加入序列,得到
- 然後刪除 ,重複第一步得到
- 直到最後剩下
,得到prufer序列
還原
仍為上面的樹,Prufer序列為{3,5,1,3},開始時G={1,2,3,4,5,6},未出現的編號最小的點是2,將2和3連邊,並刪去Prufer序列首項和G中的2。接下來連的邊為{4,5},{1,5},{1,3},此時集合G中僅剩3和6,在3和6之間連邊,原樹恢復。
題解:
由上面我們知道一個無根樹可以由
長度的
序列表示,然後每個度為d的節點出現次數為
,那麼我們可以知道除掉位置度數節點後的排列數為
,然後在每一個排列中放值第一個節點的方案數為
,放第二個節點的方案數為
,以此類推得到其他的,那麼剩餘位置度數節點的方案為
,也就是在剩餘的位置中排列即可
最後的答案為:
通過約分化簡可以得到
即為:
因為n的範圍為[1, 1000],所以要涉及到高精度的問題,我用Java大數解決的,巨佬們可以用素數優化一下。
import java.util.*;
import java.math.*;
public class Main {
public static void main(String [] args) {
Scanner cin = new Scanner(System.in);
BigInteger zero = BigInteger.ZERO, one = BigInteger.ONE;
BigInteger m = zero;
int []d = new int[1002];
BigInteger []fac = new BigInteger[1002];
fac[0] = one;
for(int i = 1; i < 1002; i++) {
fac[i] = fac[i - 1].multiply(BigInteger.valueOf(i));
}
int n = cin.nextInt(), tot = 0;
for(int i = 1; i <= n; i++) {
d[i] = cin.nextInt();
if(d[i] == -1) {
m = m.add(one);
} else {
tot = tot + d[i] - 1;
}
}
BigInteger fz = fac[n - 2].multiply(m.pow(n - 2 - tot)), fm = fac[n - 2 - tot];
for(int i = 1; i <= n; i++) {
if(d[i] == -1) continue;
fm = fm.multiply(fac[d[i] - 1]);
}
System.out.println(fz.divide(fm));
cin.close();
}
}
