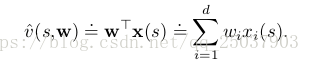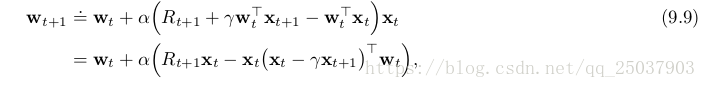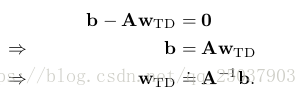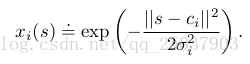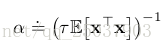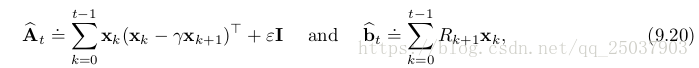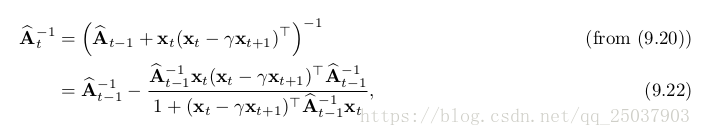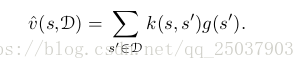強化學習（RLAI）讀書筆記第九章On-policy Prediction with Approximation

阿新 • • 發佈：2018-11-08

這一章學習使用on-policy的資料對狀態值函式進行逼近，也就是在策略 $\pi$ 下估計值函式 $v_{\pi}$ 。這一章的重點在於估計的值函式不是使用表格來表示而是使用引數w的函式形式。一般來說權重引數的數量是遠遠比狀態的數量要小的，而且改變一個權重的大小會影響到很多個狀態值的估計。於是一個值函式的更新會帶來很多其它值函式的改變。這種泛化能力非常有用但更難操作和理解。

而且把強化學習延伸到函式逼近的形式也使得它能夠應用於部分可觀測的問題，也就是agent的部分狀態是無法觀察到的。實際上本章所講的很多理論和方法都可以應用到部分觀測的問題裡。但是函式逼近不能夠使用以往觀測的記憶來改進當前狀態表示。

9.1 Value-function Approximation

本書中講到的所有預測方法都被描述為把特定狀態的值函式估計朝著一個backup值變化的過程，這個backup值也叫作update target。很自然地把每個更新過程看作是值函式對於特定輸入輸出行為的一個例子。實際更新的過程很簡單：其它狀態的值函式都不變，當前狀態的值函式向著目標值變動一個小部分。現在我們允許使用任意的複雜函式來完成這個更新的過程，並且在狀態s的更新也會導致其它很多狀態值的變化。通過這種方式來學習模仿輸入輸出樣例的機器學習方法通常叫做監督學習，當輸出是一個數字時一般叫做函式逼近。函式逼近希望能夠收到它所期望模仿的函式的輸入輸出樣例。然後我們把得到的近似函式叫做估計值函式。

把每次更新都看成一個傳統的訓練樣例能夠使我們能夠應用很多現有的值函式逼近方法。理論上我們可以使用所有監督學習的方法，包括神經網路、決策樹和其它很多多變數的迴歸函式。在強化學習中，能夠在agent與環境進行互動的同時進行線上學習是一個很重要的要求。因此需要能夠從增量式的資料中進行學習。而且強化學習還要求函式逼近能夠解決非穩態目標函式。

9.2 The Prediction Objective ( 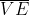$\overline{VE}$ )

在表格形式的值函式計算裡不需要一個評估估計質量的值因為學到的值函式就是精確收斂到真正的值函式的。但是在值函式的逼近中，一個狀態的更新會影響很多其它狀態，因此不可能精確得到所有的狀態值函式。因為我們假設狀態的數量遠大於引數的數量，因此讓一個狀態的估計值更精確意味著很多狀態的估計值更不精確。因此需要明確哪些狀態是我們更加關注的。因此有一個根據狀態的分佈 $\mu (s) > 0, \sum_{s}\mu(s)=1$ ，代表的是每個狀態的重要性。因此根據每個估計值和真正的狀態值之間的平方差的加權和得到了我們的目標函式均方誤差函式，用 $\overline{VE}$

表示：

$\overline{VE} \doteq \sum_{s\in S}\mu(s)\[v_{\pi}(s) - \widehat{v}(s,w) \]^{2}$

這個值的平方根給出了對於每個估計值與真值之間的誤差。一般來講 $\mu(s)$ 選擇的是在每個狀態上花費的時間佔比。對於on-policy的情況這個分佈叫做on-policy分佈也就是本章考慮的內容。對於continuing tasks，on-policy分佈一般是在策略 $\pi$ 下的固定分佈。

continuing tasks和episodic tasks雖然行為很相似，但是在值逼近中必須在正式分析中將它們分開看。也就是目標函式具體實現的不同。

目前來說還不清楚上述目標函式就是對於強化學習最適合的目標函式。因為我們的最終目標是找到最優的策略。而對應的最優的值函式不一定就是最小化VE。不過目前為止還沒找到更好的替代函式，所以還是集中在VE上。

對於優化目標函式來說最好的是得到一個全域性最優的權重，但是一般來說複雜函式很難收斂到全域性最優，因此經常會收斂到區域性最優。對於非線性函式來說，收斂到區域性最優也不能完全保證，但是通常這樣就夠了。同樣對於很多強化學習的例子中也不能保證收斂到極值或者極值的一個範圍內。有些方法實際上是發散的。

9.3 Stochastic-gradient and Semi-gradient Methods

這節講解一個具體的使用隨機梯度下降來進行函式逼近的方法。

在梯度下降法中引數是一個列向量，有固定數量的實數值， $\mathbf{w}\doteq (w_{1},w_{2},...,w_{d})^{T}$ ，用來逼近的值函式是 $\widehat{v}(s,\textbf{w})$ 。每一個離散時刻進行一次引數的更新，因此每一步的引數為 $\textbf{w}_{t}$ 。需要記住的是，沒有一組引數可以在所有的狀態上得到精確解，甚至都不可能在所有的樣本上達到完全一致。同時還需要考慮對於那些沒出現過的狀態的泛化。

假設所有出現的樣本都是在同一個分佈 $\mu$ 下產生的，在這些樣本的基礎上進行最小化均方誤差。隨機梯度下降法對於每一個出現的樣本都進行一次引數的更新：

這個梯度下降法叫做隨機的原因在於每一次只對一個樣本的結果進行更新，而這個樣本是隨機選擇的。

因為我們演算法的目標不是在所有的狀態值函式上都達到0誤差，而只是得到一個近似函式能夠平衡不同狀態值函式的誤差。因此每一次的更新都只進行一小步的更新，也就是步長引數 $\alpha$ 會很小。而且還會假設步長會隨著時間逐漸減小。如果它滿足書中公式2.7的情況，那麼這個方法能夠保證結果收斂至一個區域性極小值。

現在考慮一下目標輸出值 $U_{t}$ ，也就是狀態值的一個隨機逼近。因為我們無法知道每個狀態的精確值 $v_{\pi}(S_{t})$ ，因此沒法進行精確地像公式（9.5）中的更新，只能使用 $U_{t}$ 替換真值 $v_{\pi}(S_{t})$ 。因此實際中隨機梯度下降法的更新公式為：

只要估計值 $U_{t}$ 是真值的無偏估計，那麼在步長引數滿足2.7的情況下引數保證收斂至區域性最優值。

如果目標值的估計中使用了自舉的話就沒法像9.7式中一樣有收斂性保證。可以看到從9.4式到9.5的推導是基於括號中前一項與係數 $\textbf{w}_{t}$ 無關而得到的。但是使用了自舉來作為前一項的估計，那麼前一項就是與係數有關的。因此此時的更新只計算了一部分的梯度，所以這個方法叫做半梯度法。

儘管半梯度法不像梯度法一樣健壯地收斂，但是在一些重要的應用中比如下一節的線性情況它依然收斂。而且，因為一些優點這個方法會被優先選擇。一是這個方法一般會收斂得明顯更快。二是這種方法可以進行連續而線上的學習，不如要等待一個episode結束。演算法如下：

9.4 Linear Methods

函式逼近的一個最重要的例子是近似函式作為係數w的線性函式。線性近似方法中，狀態值近似函式是 $\textbf{w}$ 和 $\textbf{x}$ 之間的內積：

其中向量x(s)叫做狀態s的特徵向量。對於線性方法來說，特徵是奇函式，因為特徵組成了近似函式的線性基的集合。對於線性方法來說使用SGD方法是很自然的。對應9.7的係數更新公式為：

因為它的簡單，線性SGD法是最適合用來數學分析的。特別的是，線性方法中極值只有一個，因此任何保證能夠收斂至區域性最優的方法會自動保證收斂至全域性最優。上節中介紹的半梯度法TD(0)演算法同樣會線上性函式逼近中收斂，不過這是根據SGD的另一個特性。對於每一步的係數迭代為：

可以寫為另外的形式：

可以看出當係數收斂的時候

這個值叫做TD不動點。實際上半梯度法TD(0)收斂到這個點。而且這個點的存在和A的可逆在書上有證明。

在不動點上，目標函式 $\overline{VE}$ 被證明在一個值範圍以內：

也就是TD法得到的誤差不會比MC法的最小誤差大 $\dfrac{1}{1-\gamma}$ 倍。因為TD法之前講過，方差更小而且收斂得更快，因此選用哪個方法要考慮近似和問題本身以及學習過程的長短。還有一些其它on-policy的自舉方法也會收斂到相似的上限。比如線性半梯度法DP也收斂到TD不動點。半梯度法Sarsa(0)演算法收斂至相似的點與相似的上限。對於episodic tasks有一些不同但是相關的上限。對於這些收斂結果來說最重要的一點是這些狀態是根據on-policy分佈來更新的。

半梯度法n步TD演算法的虛擬碼如下：

練習9.1 係數為全為1的列向量。特徵為對應狀態的值函式，其他狀態為0。

9.5 Feature Construction for Linear Methods

線性方法不僅僅因為能夠保證收斂而有趣，更是因為在實際應用中能夠對於資料和計算都很有效率。對於特定的問題，選擇合適的特徵向量是一個重要的對強化學習系統新增先驗的方法。線性方法的一大侷限是它不能夠考慮進不同特徵之間的互動，比如有的特徵i只有在與j同時出現的時候才比較有效。

9.5.1 Polynomials

很多問題中，強化學習的函式逼近和很多插值和迴歸很像。多項式能夠組成用來插值和迴歸的最簡單的一組特徵。

比如當前問題的狀態有兩個數字維度，那麼對於每個狀態來說可以使用這兩個數字(s1,s2)表示。如果直接把他們當做狀態的特徵那麼 $\textbf{x}(s)=(s_{1},s_{2})^{T}$ ，但是這樣就不能夠體現出這兩個維度之間的互動。而且如果這兩個數字都是0，那麼這個估計值也會是0。這兩個限制都可以使用這個四維特徵來克服 $\textbf{x}(s)=(1,s_{1},s_{2},s_{1}s_{2})^{T}$ 。其中第一個1可以允許對初始狀態數字的仿射函式，而最後一項兩個數的乘積，考慮進了兩個維度的互動。也可以選擇一個含有更高維特徵的特徵向量。一般化這種選擇特徵的方式，我們可以得到使用多項式的特徵，構成方式如下：

但是由於特徵的數量會隨著維度k呈指數增長，所以只需要選擇其中一部分用來做函式逼近。

練習9.2 可以充分保證不同維度之間進行充分的互動，以及特徵1用作原狀態特徵的仿射。

練習9.3 2 4

9.5.2 Fourier Basis

另一個使用線性近似函式的方法是使用傅立葉序列，也就是把時序函式表示成不同頻率的sine基函式和cosine基函式的加權和的形式。在強化學習中，需要逼近的函式是未知的，使用傅立葉基因為用起來很簡單而且能夠在一些了強化學習問題中表現得很好。

（作為一名通訊本科的學生我沒有看懂它怎麼弄得，算了，我有罪。）

9.5.3 Coarse Coding

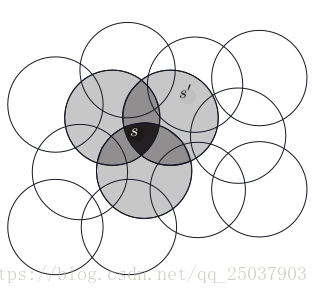
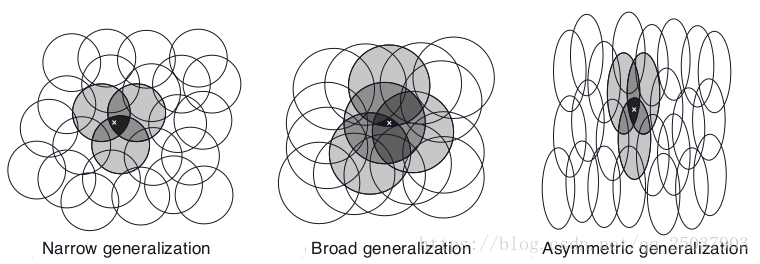
現在考慮任務是在一個自然連續的二維空間中。其中一種表示這種情況的特徵是對於空間中對應圓的表示，如右圖。如果一個狀態是在圓中，那麼該圓對應的特徵值應該是1，表示present；否則應該是0表示absent。這種1-0的特徵叫做二維特徵。對於一個給定的狀態，每個而為特徵表示的是這個狀態是否在這個圓中，於是就粗編碼了這個位置。把狀態通過這樣的重疊的特徵來表示的方法叫做粗編碼。

假設線上性梯度下降函式逼近中，考慮圓的大小和密度。對應每個圓的是會被學習演算法影響的引數。如果我們訓練一個在某個圓中的狀態，那麼所有的在這個圓中的其它狀態都會受到影響。因此對於圓比較小的情況，每個點的影響距離就比較小，而對於比較大的圓影響就比較大。而且圓的形狀也決定了泛化的特性。如下圖所示：

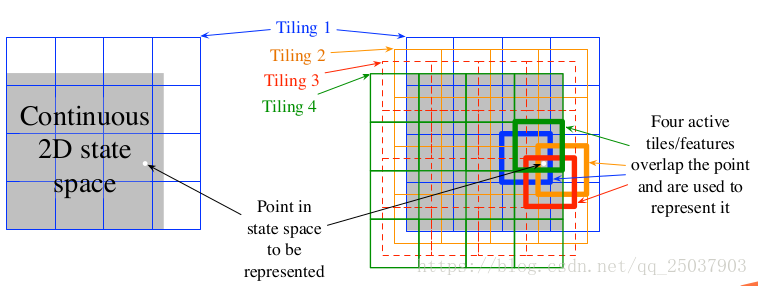
9.5.4 Tile Coding

tile coding是對於高維連續空間的一種靈活高效的coarse coding。在tile coding中每個特徵的接受範圍被劃分成一個個狀態空間的分隔。比如在最簡單的二維空間中使用一個均勻分佈的網格。這個網格是正方形的，只使用一個網格，那麼白色點可以被它落在的格子來表示。泛化會應用到格子中和格子外的所有狀態。只用一個網格我們沒有做到粗編碼而只是一個狀態聚集。

為了得到粗編碼，我們需要對接收區域進行重疊，而且不能有完全重複的網格。上圖中展示了使用四個網格的形式。每個狀態，比如上右圖中的白點，在四個網格中都落入了每個網格中的一個格子裡。而這個特徵向量對於每個網格的每個格子都有一個分量。因此在這個例子裡有4x4x4=64個分量，除了落進去的4個格子，其它每個格子對應的分量都是0。

tile coding的一個快速的實用好處在於，因為是使用的對於空間的劃分作為網格，因此對於每個狀態來說，每次活躍的特徵分量個數和網格數一樣，因為每個網格中只有一個格子被啟用。這樣也可以簡單的設定步長為網格數的倒數，可以帶來精確地one-trial learning。

同樣由於使用了二維特徵，tile coding可以獲得一定的計算優勢。特徵都是0和1，因此相加的時候非常快速。

對於其它狀態而言，當前狀態更新的時候受影響的程度和與當前狀態有共享格子的個數有關。

在選擇網格策略的時候，需要選擇網格的數量和格子的形狀。網格的數量決定了近似的精準度。而每個網格的形狀決定了泛化的特點。方格對於每個維度相同看待，而沿著一個維度逐漸拉長的網格會增加那個維度的泛化性。而對角斜紋網格會增加對角線維度的泛化性。實際應用中經常需要在不同的網格中使用不同形狀的格子。網格的選擇決定了泛化效能，直到網格能夠被自動化選擇之前，選擇更靈活而且對人類更有意義的網格很重要。

還有一種減少記憶體消耗的方式是雜湊。

練習9.4 在一個維度上網格逐漸擴大，在另一維度等分。

9.5.5 Radial Basis Functions

RBFs是對於粗編碼對於連續值特徵的自然拓展。相對於只能是0或1的特徵，RBFs特徵可以是0-1之間任意的數字。經典的RBF特徵 $x_{i}$ 作為一個高斯形式的反饋，只依賴於狀態s與設定好的中心狀態 $c_{i}$ 之間的距離以及特徵的相對寬度 $\sigma_{i}$ :

使用RBFs相對於0-1特徵的最原始的優點是它可以使得近似函式更加平滑而且可微。儘管很誘人但是實際上經常沒有實用性。

9.6 Selecting Step-Size Parameters Mannually

大多數SGD方法需要手動選擇步長引數。理論思考很不幸的沒有多大幫助。使用2.7的收斂條件可以保證收斂，但是這種情況下學習的速度太慢。在表格MC方法中設計的 $\alpha_{t}=\dfrac{1}{t}$ 不適應TD方法或者非穩態問題或者任意的函式逼近方法。對於線性方法，有一種遞迴的最小方差的方差來設定一個步長矩陣，這些方法可以延伸為一個差分學習方法叫做LSTD。因為複雜度的問題我們不在最需要函式逼近的大型問題中使用這些方法。

在表格型方法中，設定 $\alpha_{t}=\dfrac{1}{\tau}$ 來使得表格估計值利用最近 $\tau$ 步的估計值來逼近目標的均值。但是在大部分函式逼近的方法中，並沒有這麼清楚的每個狀態經驗的數量，因為每個狀態都可能與其它狀態在某些地方相似或不相似。但是線上性函式逼近中依然有一個相似的規則給出相似的行為。假設想要學習一個有相同特徵向量的狀態 $\tau$ 個經驗值，那麼應該設定線性SGD演算法的步長為

這個方法在特徵向量長度不變的時候效果最好，理想狀態是 $x^{T}x$ 為常數。

練習9.5 $\dfrac{1}{980}$

9.7 Nonlinear Frnction Approximation: Artificial Neural Networks

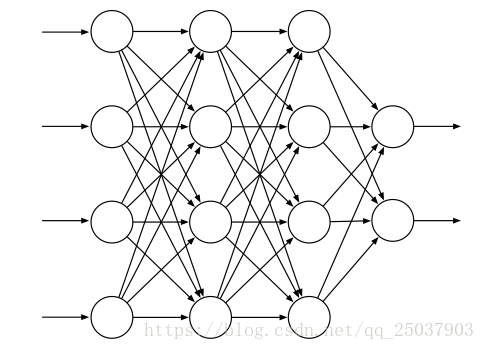
ANN是一個擁有一些神經元特性的單元連線起來的網路。第十六章介紹一些在強化學習系統中使用ANN進行函式逼近得到良好結果的例子。下圖展示了一個簡單的前饋神經網路。

每個單元一般是半線性的單元，意味著他們是輸入的甲醛和然後在結果上應用一個非線性函式，叫做啟用函式，來得到一個單元的輸出，或者啟用。一般使用的啟用函式有sigmoid和rectifier。一個沒有隱藏層的ANN只能表示很小一部分可能的輸入輸出函式。但是一個只有一層隱藏層但是有足夠多的有限數量sigmoid單元的ANN可以在網路的輸入空間上逼近輸入任何連續函式到任意精度。但是如果所有的啟用函式都是線性的，那麼ANN等同於一個沒有隱藏層的網路結構。

儘管一層隱藏層就可以逼近任何函式，但是依然選擇使用多層級聯的形式構成有多個隱藏層深度神經網路。越靠近輸出層的隱藏層計算的輸入表示就相對越抽象，而每個隱藏層單元都為整個輸入輸出函式的網路提供了一個層次的特徵表示。因此訓練一個ANN的隱藏層就相當於是對給定的問題自動的訓練特徵，而不需要完全依賴手動構造的特徵。在大部分的監督學習裡，目標函式是一個在一堆有標記的訓練樣本上期望的偏差或者損失函式。但是在強化學習裡，ANN可以使用TD誤差來學習值函式，或者可以最大化期望反饋或者進行策略梯度演算法。

使用ANN最成功的演算法是backpropagation演算法。但是bp演算法對於淺層網路效果很好，對於深層網路效果不太好。實際上訓練k+1層網路一般會比訓練k層網路得到的效果更差。原因在於，第一，深層網路的大規模的引數使得其很容易overfitting。第二，bp演算法對於深層網路效果不好，因為隨著深度加深，梯度回傳至前面的隱藏層的時候，梯度的變化由於練成會變得太小或者太大都不能得到較好的效果。

過擬合在線上強化學習問題裡不那麼明顯因為它並不是依賴於一個有限的訓練集。但是過擬合對於ANN來說是一個很大的問題因為深度網路有非常多的引數，有幾種方法可以緩和。一、當驗證集上效果開始下降時停止訓練。二、調整目標函式來抑制擬合的複雜性。三、通過增加權重之間的依賴性來減少自由度。還有一個特別有效的方法叫做dropout。指的是在訓練的過程中隨機的移除網路中的某些單元。這樣就相當於在網路中訓練了很多個更小的網路並且綜合它們的效果。這個方法需要每個隱藏層單元學習出能夠與其它特徵隨機集合都能有較好效果的特徵，因此避免了其對於特殊樣例的過擬合。

還有一種解決訓練深層網路問題的方法是使用deep brief networks，不懂跳過。

batch normalization是讓訓練深層ANN更加簡單的另一種技術。batch normalization在神經網路中對於每一個隱藏層的輸出進入下一層之前都進行歸一化。

還有個技術叫做deep residual learning。不懂跳過。

還有一種deep ANN叫做深度卷積網路。應用在影象領域很多，16章會講很多相關的樣例。

上面講到的很多ANN的設計和訓練方法，都能夠應用到強化學習的使用中。儘管目前強化學習理論大部分侷限於表格型和線性函式逼近的方法，但是著名的強化學習應用的驚人效能很多都來自於多層ANN來進行非線性函式逼近的成功應用。

9.8 Least-Squares TD

這章目前講的都是需要在每一個時間步驟進行正比於引數數量複雜度的計算。但是如果進行更多計算，演算法會得到更好結果。這節介紹一個對於線性函式近似可論證是最優的方法。

9.4節講到了線性函式逼近的TD(0)演算法會漸進收斂至TD不動點，其中。進行每步迭代計算是不必要的，可以使用一個更直接的方式來計算不動點，就是LSTD演算法。其中

$\epsilon$ 是一個很小的正數，用來保證A是可逆的。理論上講還需要除以時間t，但是在進行計算的時候分子分母可以抵消因此不需要。可以直接計算係數為。

這個演算法相比線性TD(0)法更充分利用了資料，但是需要更多的計算量。半梯度法TD(0)中每個時間步驟的計算複雜度是 $O(d)$ 。在LSTD演算法中，A和b的估計值可以使用增量形式在常數時間內完成，但是A的更新需要計算一個外積，複雜度是 $O(d^{2})$ ，空間複雜度也是這樣。而且對A求逆才是最耗時間的，時間複雜度是 $O(d^{3})$ 。幸運的是A的逆是一個特殊形式，可以使用增量式寫法，只需要 $O(d^{2})$ 複雜度的計算：

看起來很複雜，但實際上只包含了向量矩陣乘法和向量之間的乘法，因此時間複雜度是 $O(d^{2})$ ，空間複雜度也是。

當然這個時間複雜度依然是非常大的消耗，但是演算法對於資料的高效利用是值得這個計算消耗的。LSTD演算法不需要步長引數，這一點經常被吹捧，但是卻需要一個 $\epsilon$ 。 $\epsilon$ 太小，求逆的結果可能會變化很大， $\epsilon$ 太大學習的速度就會很慢。而且沒有步長意味著LSTD演算法不會遺忘，有時候這一點是需要的。在control演算法中LSTD法需要結合其它的機制來引入遺忘，使得不需要步長的優點毫無意義。

9.9 Memory based Function Approximation

我們目前講的都是引數化的方法來逼近值函式。但是基於記憶的方式不同，它們只需要儲存演算法訪問過的訓練樣本（的一部分）而不需要更新任何引數。當需要查詢某個狀態的值估計的時候，利用記憶中的過往樣本來計算出這個狀態的值即可。這個方式有時也叫作lazy learning因為知道系統需要輸出時才對訓練樣本進行處理。

和引數化方法不同，基於記憶的方法的近似函式並不侷限於一類固定引數的函式，而是有訓練樣本來決定。通過組合過往的訓練樣本來輸出查詢狀態的狀態值。訓練樣本越多，非引數化方法的結果就越精確。

有很多種基於記憶的演算法。我們關注一種local-learning的演算法。這些演算法通過利用查詢狀態附近的鄰居來逼近值函式。從樣本中先提取出和查詢狀態相近的樣本，然後可以根據距離賦予權重，之後組合這些鄰近樣本給出查詢結果。結果隨後丟棄。最簡單的基於記憶的方式叫做最近鄰居法。就是直接返回和需要查詢的狀態最接近的狀態的結果。稍微複雜點的方式就是抽取一堆比較鄰近的樣本，然後輸出他們的加權平均。locally weighted regression也是類似，只不過是在附近的狀態集合上擬合出一個平面來得到結果。之後這個平面也會被丟棄。

作為非引數化的方法，基於記憶的演算法相對引數化方法有很多優點。比如隨著資料增多，精準度會越來越高。而且非引數法可以更適應強化學習演算法。比如在Trajectory sampling中，非引數化的結果可以更關注那些真實軌跡中訪問過的狀態。而且非引數法可以使得樣本對於鄰近狀態的影響更直接，而不像引數法那樣需要增量式調整引數來得到全域性近似。

避免全域性近似也是一個解決維度災難的好方法。非引數法儲存n個樣本只需要正比於n的空間，但是對於有k維的樣本空間，引數法需要解決指數級的引數或者狀態空間。當然還有個關注點就是非引數法是否能夠快速相應對狀態的查詢。在一個很大的資料集中查詢最鄰近節點需要太長的時間。

使用平行計算可以加速最鄰近節點的查詢，特殊的多維資料結構如kd樹就是個快速查詢的例子。locally weighted regression額外需要找到快速計算迴歸的方式。

9.10 Kernel-based Function Approximation

上節講的基於記憶的加權平均和加權迴歸法都依賴於對於兩個狀態之間賦予一個權重的演算法。這個賦予權重的函式叫做核函式，或者叫做一個核。稍微不同的看待的話，核函式 $k(s,s')$ 是計算從s’到s泛化能力的計算。核函式計算出任何兩個狀態之間關聯知識程度的數值表達。

kernel regression是一個計算記憶中所有樣本核加權平均然後將結果賦值給查詢狀態的基於記憶的方法。

一個常用的核叫做高斯射線基函式（RBF），和RBF函式逼近用到的一樣。函式逼近的形式是一個預先定義的RBFs的線性組合。每個基的引數可以通過SGD的方法進行學習。但是使用RBF核函式的kernel regression不一樣，首先它是基於記憶的：RBF是以儲存過的樣例狀態為中心的。第二：它是非引數化的：沒有引數需要學習，只需要給出一個查詢反饋。

任何線性引數迴歸的方法，比如9.4中講的那種把狀態表示為一個特徵向量形式的，都可以重寫為kernel regression的形式，其中核函式k(s,s')是特徵向量的內積，也就是。重寫為kernel regression的線性引數方法如果使用同樣的學習樣本會得到相同的結果。

我們可以直接構造核函式而不需要考慮任何的特徵向量。不是所有的核函式都能夠表示為特徵向量的內積，但是那些可以表現為特徵向量內積的核函式能夠提供相對引數方法更重要的優勢。很多特徵向量有一個更加簡潔的函式形式而不需要在一個d維空間中進行計算。在這些例子裡，kernel regression比直接使用這些特徵向量的線性引數表示更簡單。這叫做核技巧，能夠更高效的基於已知訓練樣本在高維的高消耗的特徵空間中計算。這是很多機器學習方法的基礎。

9.11 Looking Deeper at On-policy Learning: Interest and Emphasis

目前講到的演算法都把每個遇到的狀態都平等看待，就像它們是一樣重要一樣。但是有些例子裡我們更關注某些特定的狀態。比如在discounted episodic的問題裡，我們可能更關注更早訪問的狀態的值，因為後面狀態的值被設定的很小。函式逼近的計算力是有限的，因此我們需要更加關注那些能夠有效提高效能的狀態。

我們把目前遇到的狀態都平等看待的一個原因是我們目前根據on-policy分佈進行更新。在這個分佈上能夠得到半梯度法更強的理論結果。現在介紹幾個新概念。一個是介紹一個非負的標量值，叫做interest的一個隨機變數 $I_{t}$ ，代表的是在時間t時我們關注當前狀態的程度。於是9.1節中的均方誤差函式VE中的分佈 $\mu$ 就定義為根據遵循當前目標策略下遇到狀態的分佈根據Interest加權得到的結果。第二定義另一個非負的標量隨機變數，emphasis $M_{t}$ 。這個標量乘以每次更新時候的誤差來表示對這次學習的重視程度。比如n步更新可以寫為：

其中emphasis的定義為：

9.12 Summary

如果想要強化學習能夠應用到AI或者大型的更稱應用中，強化學習就必須有足夠的泛化能力。為了達到這個目的，目前的監督學習方法都可以將每次更新看做一個樣本來作為監督學習的函式逼近。

最適合的監督學習方法可能是使用引數的函式逼近。其中策略被引數化為權重向量w。定義了均方誤差函式作為函式逼近的衡量方式。為了找到更合適的權重向量，最流行的方式是隨機梯度下降法。這章關注on-policy基於一個固定策略的形式，叫做prediction或者evaluation。在這種形式裡最自然的演算法是n步半梯度TD法，它包含了MC和半梯度TD(0)。

使用半梯度法可以線上性函式逼近中得到很好的結果。線性函式逼近的結果就是特徵向量的引數加權和。線性情況有很好的理論研究結果。特徵向量的選擇是一個非常重要的往強化學習中新增先驗的形式。主要方法有多項式法（在線上學習力泛化能力差），傅立葉基（需要重複分隔範圍的粗編碼），tile coding法和Radial basis函式法。LSTD演算法是一個最有效的線性TD預測演算法，不過需要平方級別的計算複雜度。非線性方法比如神經網路在最近幾年通過深度強化學習的方式也變得很火。

線性半梯度n步TD演算法保證收斂至一個最優誤差的範圍內。n越大誤差越小。但是更大的n會使得學習更慢，因此實際中一定程度的自舉會更好。

強化學習（RLAI）讀書筆記第九章On-policy Prediction with Approximation

9.1 Value-function Approximation

9.2 The Prediction Objective ( $\overline{VE}$ )

9.3 Stochastic-gradient and Semi-gradient Methods

9.4 Linear Methods