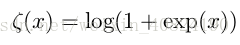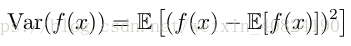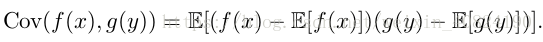當方差很小時,f (x) 的值形成的簇比較接近它們的期望值。方差的平方根被稱為標準差(standard deviation)。

協方差(covariance)在某種意義上給出了兩個變數線性相關性的強度以及這些變數的尺度:

        協方差的絕對值如果很大則意味著變數值變化很大並且它們同時距離各自的均值很遠。如果協方差是正的,那麼兩個變數都傾向於同時取得相對較大的值。如果協方差是負的,那麼其中一個變數傾向於取得相對較大的值的同時,另一個變數傾向於取得相對較小的值,反之亦然。其他的衡量指標如 相關係數(correlation)將每個變數的貢獻歸一化,為了只衡量變數的相關性而不受各個變數尺度大小的影響。

        兩個變數如果相互獨立那麼它們的協方差為零,如果兩個變數的協方差不為零那麼它們一定是相關的。然而,獨立性又是和協方差完全不同的性質。兩個變數相互依賴但具有零協方差是可能的。

3.9 常用概率分佈

3.9.1 Bernoulli 分佈

Bernoulli 分佈 (Bernoulli distribution)是單個二值隨機變數的分佈。它由單個引數 φ ∈ [0, 1] 控制,φ 給出了隨機變數等於 1 的概率。它具有如下的一些性質: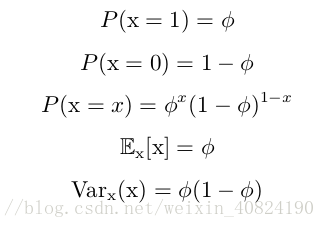

x	0	1
P	1-φ	φ

3.9.1 Multinoulli 分佈

3.9.3 高斯分佈

實數上最常用的分佈就是正態分佈(normal distribution),也稱為高斯分佈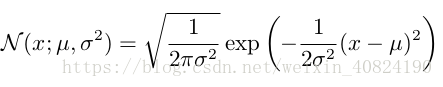(Gaussian distribution):正態分佈由兩個引數控制,μ ∈ R 和 σ ∈ (0, ∞)。引數 μ 給出了中心峰值的座標,這也是分佈的均值:E[x]=μ。分佈的標準差用 σ 表示,方差用 σ 2 表示。 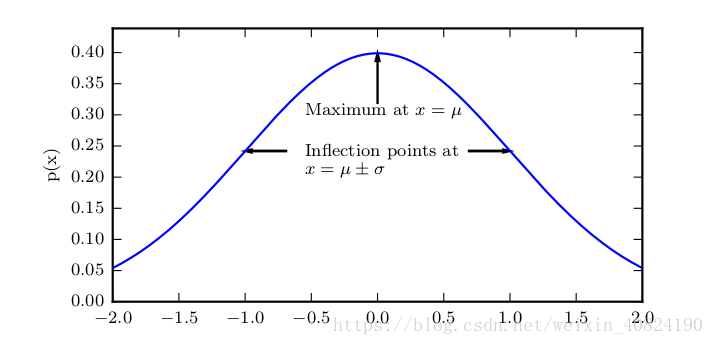       正態分佈 N (x; μ, σ 2 ) 呈現經典的 ‘鐘形曲線’ 的形狀,其中中心峰的 x 座標由 μ 給出,峰的寬度受 σ 控制。在這個示例中,我們展示的是 標準正態分佈(standard normaldistribution),其中 μ = 0, σ = 1。

        採用正態分佈在很多應用中都是一個明智的選擇。當我們由於缺乏關於某個實數上分佈的先驗知識而不知道該選擇怎樣的形式時,正態分佈是預設的比較好的選擇,其中有兩個原因。

第一,我們想要建模的很多分佈的真實情況是比較接近正態分佈的。 中心極限定理(central limit theorem)說明很多獨立隨機變數的和近似服從正態分佈。這意味著在實際中,很多複雜系統都可以被成功地建模成正態分佈的噪聲,即使系統可以被分解成一些更結構化的部分。

第二,在具有相同方差的所有可能的概率分佈中,正態分佈在實數上具有最大的不確定性。因此,我們可以認為正態分佈是對模型加入的先驗知識量最少的分佈。

3.10 常用函式的有用性質

某些函式在處理概率分佈時經常會出現,尤其是深度學習的模型中用到的概率分佈。
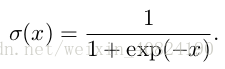
其中一個函式是 logistic sigmoid 函式: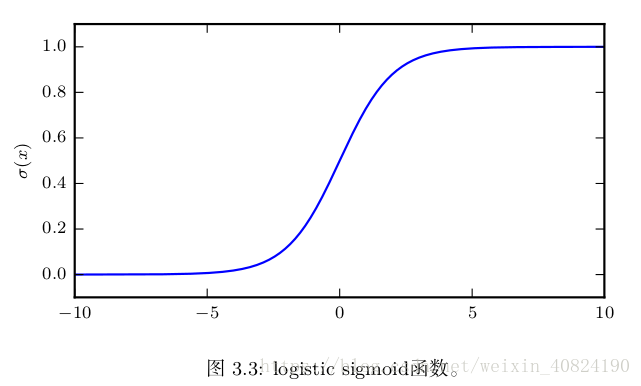另外一個經常遇到的函式是 softplus 函式：