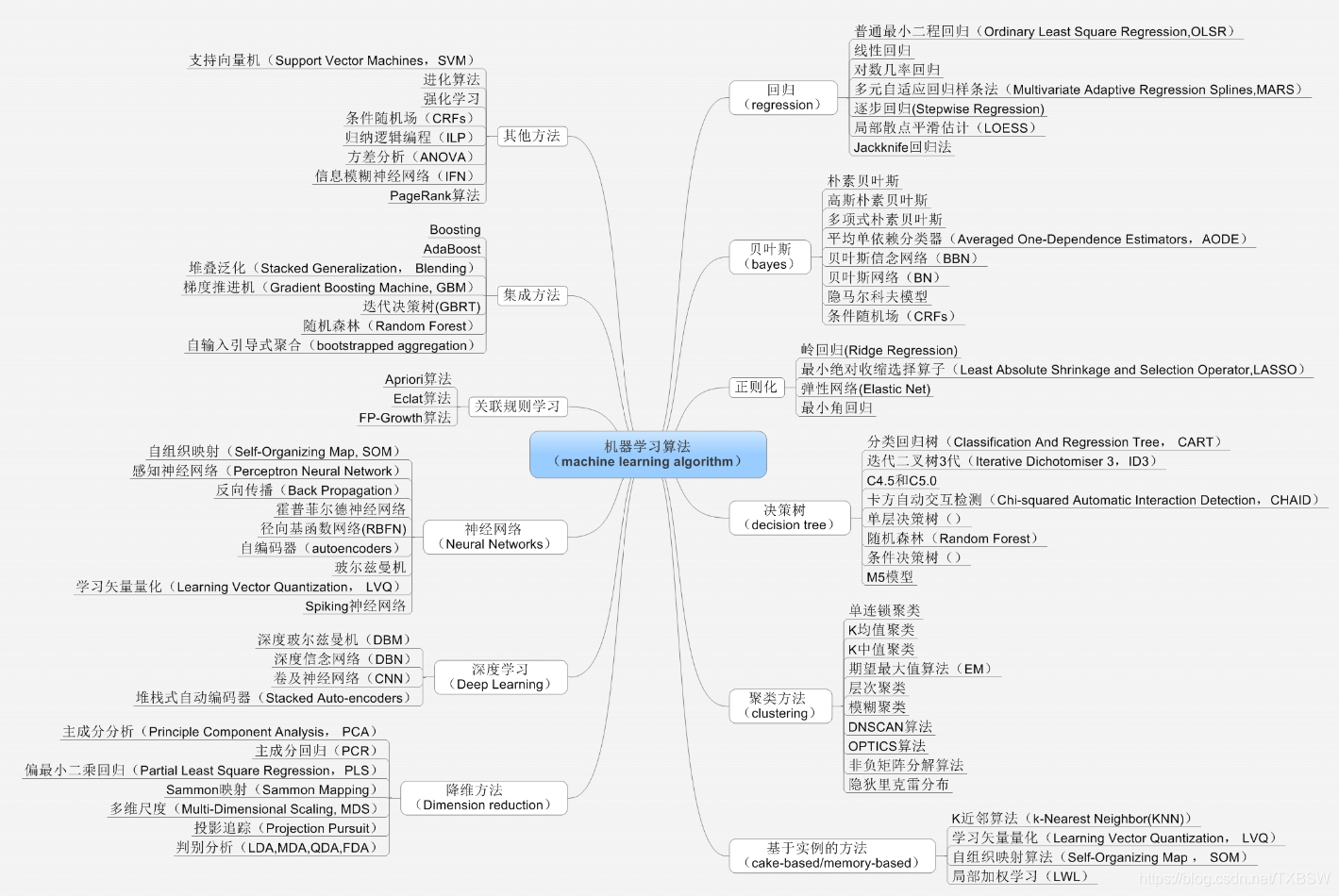
機器學習入門篇
阿新 • • 發佈:2018-11-08
題外話:第二次純手打編輯部落格啦!
以下內容摘自百度百科:
AI概念:
- 人工智慧(Artificial Intelligence),英文縮寫為AI。它是研究、開發用於模擬、延伸和擴充套件人的智慧的理論、方法、技術及應用系統的一門新的技術科學。
機器學習:
- 機器學習(Machine Learning, ML)是一門多領域交叉學科,涉及概率論、統計學、逼近論、凸分析、演算法複雜度理論等多門學科。專門研究計算機怎樣模擬或實現人類的學習行為,以獲取新的知識或技能,重新組織已有的知識結構使之不斷改善自身的效能
它是人工智慧的核心,是使計算機具有智慧的根本途徑,其應用遍及人工智慧的各個領域,它主要使用歸納、綜合而不是演繹。
深度學習:
- 深度學習的概念由Hinton等人於2006年提出。基於深度置信網路(DBN)提出非監督貪心逐層訓練演算法,為解決深層結構相關的優化難題帶來希望,隨後提出多層自動編碼器深層結構。此外Lecun等人提出的卷積神經網路是第一個真正多層結構學習演算法,它利用空間相對關係減少引數數目以提高訓練效能。[1]
深度學習是機器學習中一種基於對資料進行表徵學習的方法。觀測值(例如一幅影象)可以使用多種方式來表示,如每個畫素強度值的向量,或者更抽象地表示成一系列邊、特定形狀的區域等。而使用某些特定的表示方法更容易從例項中學習任務(例如,人臉識別或面部表情識別)。深度學習的好處是用非監督式或半監督式的特徵學習和分層特徵提取高效演算法來替代手工獲取特徵。
深度學習是機器學習研究中的一個新的領域,其動機在於建立、模擬人腦進行分析學習的神經網路,它模仿人腦的機制來解釋資料,例如影象,聲音和文字。[2]
同機器學習方法一樣,深度機器學習方法也有監督學習與無監督學習之分.不同的學習框架下建立的學習模型很是不同.例如,卷積神經網路(Convolutional neural networks,簡稱CNNs)就是一種深度的監督學習下的機器學習模型,而深度置信網(Deep Belief Nets,簡稱DBNs)就是一種無監督學習下的機器學習模型。 -
切入正題:
作為一個還未入門的小白來說的我,一直認為,人工智慧很高大上!下面就講一下我從完全不懂AI到逐漸瞭解的過程吧
一開始是什麼都不懂,不知道自己的學習路線,也完全不知道人工智慧包括一些什麼東西,就只能自己問度娘,雖然現在還是一知半解吧!首先呢講一下我們要進軍AI領域我們應該具備一些什麼基礎:首先需要會一門程式語言(我個人推薦python語言,因為python的庫很多)
我個人就是從python的庫開始瞭解AI的,首先了解numpy ,matplotlib這兩個庫
一個用python實現的科學計算包。包括:1、一個強大的N維陣列物件Array;2、比較成熟的(廣播)函式庫;3、用於整合C/C++和Fortran程式碼的工具包;4、實用的線性代數、傅立葉變換和隨機數生成函式。numpy和稀疏矩陣運算包scipy配合使用更加方便
NumPy(Numeric Python)提供了許多高階的數值程式設計工具,如:矩陣資料型別、向量處理,以及精密的運算庫。專為進行嚴格的數字處理而產生。多為很多大型金融公司使用,以及核心的科學計算組織如:Lawrence Livermore,NASA用其處理一些本來使用C++,Fortran或Matlab等所做的任務
我個人就認為是個畫圖用的。。。。就不給你們專業的講了
然後從網上入手一份鄒博老師的機器學習視訊課程觀看,每一節課比較長(一般兩個多小時。。容易犯困,裡面很多數學公式看不懂)所以在此提出,我們還需要補一下高數,概率論,線性代數
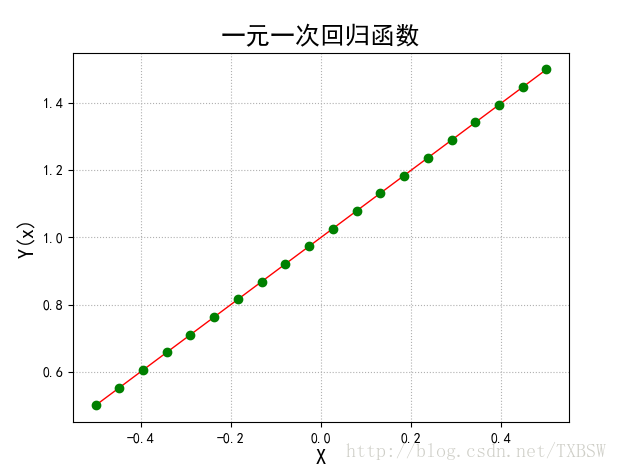
廢話不多說直接上個乾貨,我自己寫的一個最簡單的一元一次線性迴歸函式:
import numpy as np
import tensorflow as tf
import matplotlib as mpl
import matplotlibpyplot as plt
#從-0.5到0.5之間生成20個隨機點
x_data = np.linspace(-0.5,0.5,20)[:, np.newaxis]
y_data = x_data +1
plt.figure()
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.plot(x_data,y_data,'r-',x_data,y_data,'go',lw=1)
plt.title(u'一元一次迴歸函式',fontsize=18)
plt.xlabel('X',fontsize=15)
plt.ylabel('Y(x)',fontsize=15)
plt.grid(True,ls=":")
plt.show()
結果:
import numpy as np
import matplotlib.pyplot as plt
x = np.array([30,35,37, 59, 70, 76, 88, 100]).astype(np.float32)
print("x=:",x)
y = np.array([1100, 1423,1377,1800,2304,2588,3495,4839]).astype(np.float32)
print("====="*30)
print("y=:",y)
plt.rcParams['font.sans-serif']=['SimHei'] #用來正常顯示中文標籤
plt.rcParams['axes.unicode_minus']=False #用來正常顯示負號
x_max = max(x)
x_min = min(x)
y_max = max(y)
y_min = min(y)
#實際演算法
for i in range(0,len(x)):
x[i] = (x[i] - x_min)/(x_max - x_min)
y[i] = (y[i] - y_min)/(y_max - y_min)
print("****"*30)
print("new(x):%s \nnew(y):%s"%(x,y))
a = 1
b = -0.15
#X軸與Y軸
y_ , x_ = np.array([0,1]),np.array([0,1])
#迴歸方程式
yp = a*x +b
r = sum(np.square(np.round(yp-y,4)))#square取平方
print("****"*30)
#就是新的x減掉新的y保留小數點後4位
print(np.round(yp-y,4))
print("****"*30)
print(np.square(np.round(yp-y,4)))
print(r/16)
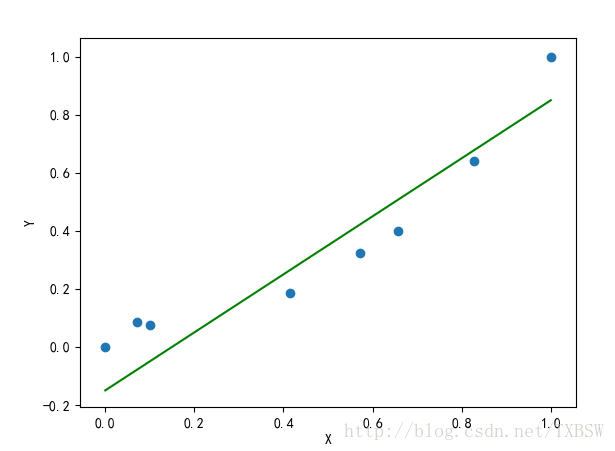
plt.scatter(x,y)
plt.xlabel(u"X")
plt.ylabel(u"Y")
plt.plot(x,yp,"r-",color='green')
plt.show()
#程式執行5秒
#plt.pause(5)
結果:
控制檯輸出:
x=: [ 30. 35. 37. 59. 70. 76. 88. 100.]
==================================================================================================
y=: [ 1100. 1423. 1377. 1800. 2304. 2588. 3495. 4839.]
**************************************************************************************************
new(x):[ 0. 0.07142857 0.1 0.41428572 0.5714286 0.65714288
0.82857144 1. ]
new(y):[ 0. 0.08638673 0.07408398 0.18721583 0.32201123 0.39796737
0.64054561 1. ]
**************************************************************************************************
[-0.15000001 -0.16500001 -0.1241 0.0771 0.0994 0.1092 0.038
-0.15000001]
**************************************************************************************************
[ 0.0225 0.027225 0.01540081 0.00594441 0.00988036 0.01192464
0.001444 0.0225 ]
0.00730120158551