【題目描述】

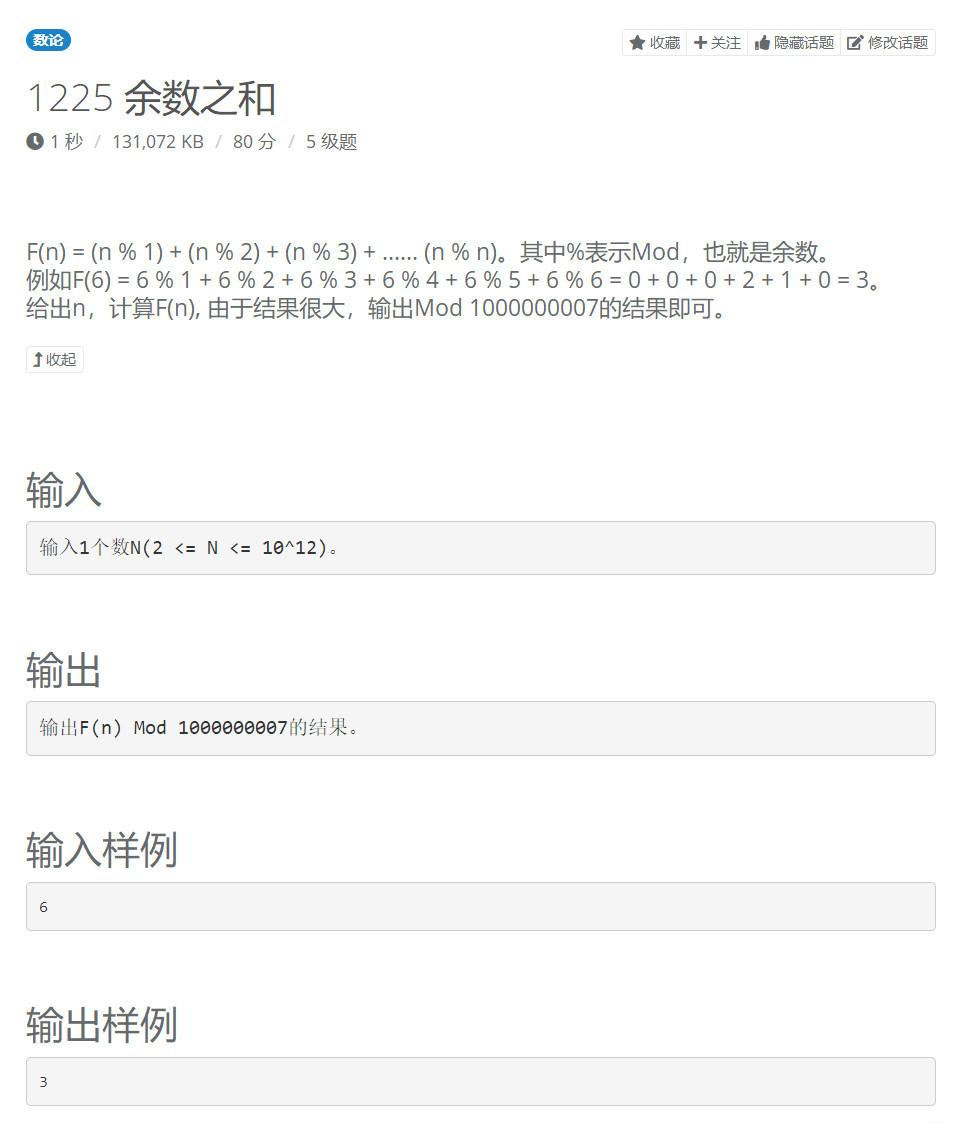
【思路】
整除分塊+等差數列
設 $p=\lfloor \frac{k}{i}\rfloor ,$

#include<bits/stdc++.h>
using namespace std;
const long long mod=1000000007;

int main(){
	long long n,ans=0,inv2=(mod+1)/2;
	scanf("%lld",&n);
	for(long long L=1,R;L<=n;L=R+1){
		R=n/(n/L);
		ans=(ans+(R-L+1)%mod*((n%L+n%R)%mod)%mod*inv2%mod)%mod;
	}
	printf("%lld\n",ans);
	return 0;
}