【Luogu P1502】 視窗的星星
(複製一下題面好了~)

題目背景
小卡買到了一套新房子,他十分的高興,在房間裡轉來轉去。
題目描述
晚上,小卡從陽臺望出去,“哇~~~~好多星星啊”,但他還沒給其他房間設一個窗戶,天真的小卡總是希望能夠在晚上能看到最多最亮的星星,但是窗子的大小是固定的,邊也必須和地面平行。這時小卡使用了超能力(透視術)知道了牆後面每個星星的位置和亮度,但是小卡發動超能力後就很疲勞,只好拜託你告訴他最多能夠有總和多亮的星星能出現在視窗上。
輸入輸出格式
輸入格式:
本題有多組資料,第一行為T 表示有T組資料T<=10
對於每組資料
第一行3個整數n,W,H,(n<=10000,1<=W,H<=1000000)表示有n顆星星,視窗寬為W,高為H。
接下來n行,每行三個整數xi,yi,li 表示星星的座標在(xi,yi),亮度為li。(0<=xi,yi<2^31)
輸出格式:
T個整數,表示每組資料中視窗星星亮度總和的最大值。
輸入輸出樣例
輸入樣例#1:輸出樣例#1:2 3 5 4 1 2 3 2 3 2 6 3 1 3 5 4 1 2 3 2 3 2 5 3 1
5 6
說明
小卡買的窗戶框是金屬做的,所以在邊框上的不算在內。
喜歡這個題目背景~
這類題目有一個很巧妙的轉化,把移動的視窗(面)和星星(點)轉成 可以覆蓋到星星的(面)和視窗的左下角(點)
什麼意思呢?(可以結合下面的圖片理解)
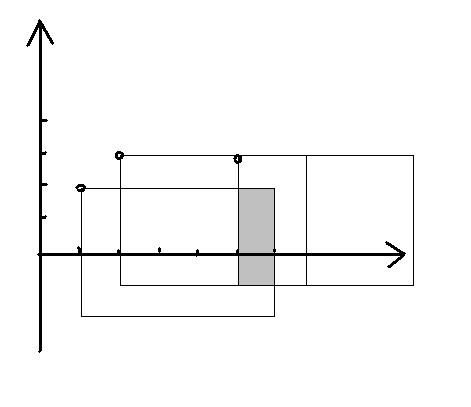
把每一個星星作為右上角,在它的左下方劃出一片視窗大小的區域,表示只要視窗的左下角落在這一片區域裡就一定能覆蓋到這顆星星。
那麼不同星星的重疊部分就代表能同時覆蓋這幾顆星星了。
(下圖中,只要視窗落在陰影部分,就能同時覆蓋到三顆星星)
所以這一題的解法就是:
想象一條掃描線從左掃到右邊,只要進入了星星的區域,掃描線上這段區間就可以取到這顆星星的值,等過了區域再減去這顆星星的值。
那就可以用線段樹來做啦,每次挪動找出區間的最值更新答案就可以了。
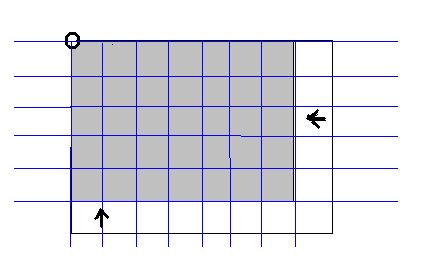
看到題目最後的提示:小卡買的窗戶框是金屬做的,所以在邊框上的不算在內。(驚!
邊框居然不算,好吧那就只好把範圍縮小,到了陰影部分外的那條平行y軸的線就可以把這顆星星的貢獻減掉了。(用Windows XP 畫的的圖,有點醜)
還有,星星的座標很大,記得離散化。
具體操作細節可以看程式碼(用了vector來維護座標上加和減的星星)
(程式碼雖然很長,但結構還算清晰吧)
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<vector> 6 #include<algorithm> 7 8 #define For(i,a,b) for(int i=a;i<=b;++i) 9 #define Pn putchar('\n') 10 #define llg long long 11 12 using namespace std; 13 14 const int N=2e4+10; 15 16 struct LIS{ 17 int x,y,id; 18 }Lis[N*2]; 19 20 struct Star{ 21 int x1,x2,y1,y2; 22 llg lgt; 23 Star(){ 24 x1=0; x2=0; y1=0; y2=0; 25 lgt=0; 26 } 27 }st[N]; 28 29 vector<int>ads[N]; 30 vector<int>mns[N]; 31 32 int tot=0,n,m,W,H,x,y; 33 llg tag[N*4],mx[N*4],ans=0; 34 35 void read(int &v){ //讀入優化,和輸出優化 36 v=0; bool fg=0; 37 char c=getchar(); if(c=='-')fg=1; 38 while(c<'0'||c>'9'){c=getchar(); if(c=='-')fg=1;} 39 while(c>='0'&&c<='9'){v=v*10+c-'0',c=getchar();if(c=='-')fg=1;} 40 if(fg)v=-v; 41 } 42 void read(llg &v){ 43 v=0; bool fg=0; 44 char c=getchar(); if(c=='-')fg=1; 45 while(c<'0'||c>'9'){c=getchar(); if(c=='-')fg=1;} 46 while(c>='0'&&c<='9'){v=v*10+c-'0',c=getchar();if(c=='-')fg=1;} 47 if(fg)v=-v; 48 } 49 void write(int x){ 50 if(x>9)write(x/10); 51 int xx=x%10; 52 putchar(xx+'0'); 53 } 54 //排序 55 bool cmpX(const LIS &a,const LIS &b){ 56 return a.x<b.x; 57 } 58 bool cmpY(const LIS &a,const LIS &b){ 59 return a.y<b.y; 60 } 61 //線段樹操作 62 void pDown(int o){ 63 llg tg=tag[o]; tag[o]=0; 64 int ls=o<<1,rs=o<<1|1; 65 tag[ls]+=tg; tag[rs]+=tg; 66 mx[ls]+=tg; mx[rs]+=tg; 67 } 68 void Ins(int o,int l,int r,int lx,int rx,llg dt){ 69 if(lx<=l&&rx>=r){ 70 mx[o]+=dt; tag[o]+=dt; 71 return; 72 } 73 int m=(l+r)>>1; 74 int ls=o<<1,rs=o<<1|1; 75 if(tag[o])pDown(o); 76 if(lx<=m)Ins(ls,l,m,lx,rx,dt); 77 if(rx>m)Ins(rs,m+1,r,lx,rx,dt); 78 mx[o]=max(mx[ls],mx[rs]); 79 } 80 81 int main(){ 82 int T; read(T); 83 while(T--){ 84 tot=0; ans=0; 85 memset(tag,0,sizeof(tag)); 86 memset(mx,0,sizeof(mx)); 87 88 read(n); read(W); read(H); 89 For(i,1,n){ //存下星星區域的右上角和左下角 90 read(x); read(y); read(st[i].lgt); 91 st[i].x1=st[i].x2=st[i].y1=st[i].y2=0; 92 Lis[++tot].x=x; 93 Lis[tot].y=y,Lis[tot].id=i; 94 95 Lis[++tot].x=x+W-1; 96 Lis[tot].y=y-H+1,Lis[tot].id=i; 97 } 98 Lis[0].x=-2147483600; 99 Lis[0].y=-2147483600; 100 101 sort(Lis+1,Lis+tot+1,cmpY); //分別對X和Y離散化 102 int ty=0; 103 For(i,1,tot){ 104 if(Lis[i].y!=Lis[i-1].y)ty++; 105 int ID=Lis[i].id; 106 if(!st[ID].y2){ 107 st[ID].y2=ty; 108 }else{ 109 st[ID].y1=ty; 110 } 111 } 112 113 sort(Lis+1,Lis+tot+1,cmpX); 114 int tx=0; 115 For(i,1,tot){ 116 if(Lis[i].x!=Lis[i-1].x)tx++; 117 int ID=Lis[i].id; 118 if(!st[ID].x1){ 119 st[ID].x1=tx; 120 }else{ 121 st[ID].x2=tx; 122 } 123 } 124 125 For(i,1,tx+1){ //初始化vector 126 ads[i].clear(); 127 mns[i].clear(); 128 } 129 130 For(i,1,n){ 131 int lx,rx; //把星星掛到相應的橫座標上 132 lx=st[i].x1; //ads為加, mns為減 133 rx=st[i].x2+1; 134 ads[lx].push_back(i); 135 mns[rx].push_back(i); 136 } 137 For(i,1,tx){ 138 int sz; 139 140 sz=mns[i].size(); 141 For(j,0,sz-1){ //先減後加 142 int ID=mns[i][j]; 143 int lx,rx; 144 lx=st[ID].y2; 145 rx=st[ID].y1; 146 Ins(1,1,ty,lx,rx,-st[ID].lgt); 147 148 } 149 150 sz=ads[i].size(); 151 For(j,0,sz-1){ 152 int ID=ads[i][j]; 153 int lx,rx; 154 lx=st[ID].y2; 155 rx=st[ID].y1; 156 Ins(1,1,ty,lx,rx,st[ID].lgt); 157 } 158 ans=max(ans,mx[1]); 159 } 160 write(ans); Pn; 161 } 162 return 0; 163 }
