有一批集裝箱,要裝上一艘載重量為c的輪船。其中集裝箱i的重量為wi。

最優裝載問題要求確定在裝載體積不受限制的情況下，將盡可能多的集裝箱裝上輪船。

最優裝載問題問題的形式描述：

•問題的形式描述是：給定c＞0，wi＞0，1≤i≤n，求n元0-1向量

     (x1, x2, …, xn)，使得

輸入：集裝箱的數目n，船的載重量c，集裝箱i的重量為wi。

輸出：集裝箱i是否裝船，是的話輸出1，反之輸出0.

執行結果：

最優裝載問題可用貪心演算法求解。採用重量最輕者先裝的貪心選擇策略，可產生最優裝載問題的最優解。

根據w從小到大排序，t中儲存陣列下標,用的是簡單的氣泡排序。

template <class Type>
void Sort(Type *w, Type *t, int n)
{
    int i, j;

    for(i = 1; i <= n; i++)
        t[i] = i;
    for(i = 1; i <= n; i++)
        for(j = i+1; j <= n; j++)
            if(w[t[i]] > w[t[j]])
                swap(t[i], t[j]);
}

主要計算量為按照重量從小到大排序，演算法時間複雜度O(nlogn).

template <class Type>
void Loading(int *x, Type *w, Type c, int n)
{
    int *t, i;

    t = new int[n+1];
    for(i = 1; i <= n; i++)                  //初值
        x[i] = 0;
    Sort(w, t, n);                           //t按重量排序的陣列下標
    for(i = 1; i <= n && w[t[i]] <= c; i++)
    {
        x[t[i]] = 1;
        c -= w[t[i]];
    }
}
 

貪心選擇性質:

設集裝箱已按其重量由小到大排序, (x1, x2, …, xn)是最優裝載問題的一個最優解. 令

若給定最優裝載問題有解, 則1≤k ≤n.

 (1) 當k=1時, (x1, x2, …, xn)是一個滿足貪心選擇性質的最優解;

 (2) 當k>1時, 取y1=1, yk=0, yi=xi, 1<i≤n, i≠k, 則

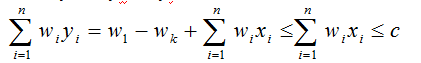
故(y1, y2, …, yn)是所給最優裝載問題的一個可行解.

而由(y1+ y2+ … + yn)= (x1+ x2+ …+ xn)知, (y1, y2, …, yn)是一個滿足貪心選擇性質的最優解.

最優裝載問題具有貪心選擇性質。

最優子結構性質:

若(x1, x2, …, xn)是最優裝載問題的一個滿足貪心選擇性質的最優解, 則有x1=1。

 (x2, …, xn)是輪船載重量為c-w1且待裝集裝箱為{2, 3, …, n}時, 相應最優裝載問題的一個最優解.

最優裝載問題具有最優子結構性質。

由最優裝載問題的貪心選擇性質和最優子結構性質，容易證明演算法loading的正確性。

演算法loading的主要計算量在於將集裝箱依其重量從小到大排序，故演算法所需的計算時間為 O(nlogn)。