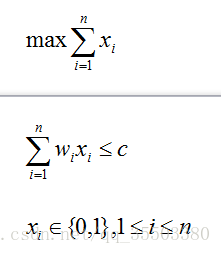演算法之最優裝載
阿新 • • 發佈:2018-12-18
1.問題描述:有一批集裝箱要裝上一艘載重量為c的輪船,其中集裝箱i的重量為wi。最優裝載問題要求在裝載體積不受限制的情況下,將盡可能多的集裝箱裝上輪船。
該問題可以形式化描述為:
式中xi=0表示不裝入集裝箱i,xi=1表示裝入集裝箱i。
2.問題分析:因為體積不受限制,每個集裝箱除重量外都一樣,所以為了裝儘可能的集裝箱,可以優先選擇重量最輕的集裝箱裝入,依次類推。
3.貪心選擇性質:每次選擇重量最輕的集裝箱裝入,即每次選擇區域性最優的解,最終可以得到該問題的最優解。
4.最優子結構性質:設(y1,y2,…,yn)是所給0-1揹包問題的一個最優解,則(y2,y3,…,yn)是如下子問題的一個最優解:
#include <iostream> using namespace std; void Loading(int x[],int w[],int c,int n) { //可以先對w進行排序 int weight=0; for(int i=0;i<n;i++) { weight+=w[i]; if(weight<=c)x[i]=1; else x[i]=0; } } int main() { int w[]={1,2,3,4,5,6}; int x[6],c=10,n=6; Loading(x,w,c,n); for(int i=0;i<n;i++) cout<<x[i]<<" "; }
複雜度分析:主要體現在排序上