在一個2k×2k 個方格組成的棋盤中，恰有一個方格與其它方格不同，稱該方格為一特殊方格，且稱該棋盤為一特殊棋盤。

用4種不同形態的L型骨牌, 覆蓋給定特殊棋盤上除特殊方格以外的所有方格，且任何2個不得重疊。

輸入：特殊方格的位置（0-size-1），方格的大小size

輸出：各個方格所屬的骨牌的編號，骨牌的編號由放置的順序決定，越早放編號越小。特殊方格由-1表示。

執行結果：

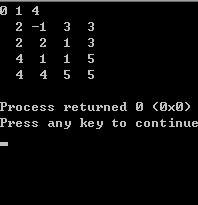
當k>0時，將棋盤分割成 4 個子棋盤

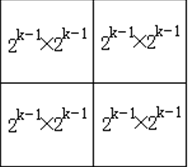
特殊方格必位於4個較小子棋盤之一中，其餘3個子棋盤中無特殊方格。

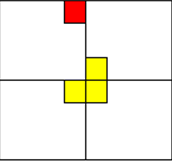
為將無特殊方格子棋盤轉化為特殊棋盤，可以用一個骨牌覆蓋3個較小棋盤的回合處，從而將原問題轉化為3個較小規模的棋盤覆蓋問題。

遞迴地使用這種分割，直至棋盤簡化為棋盤 1 * 1。

int board[10][10];     //棋盤 （0,0）表示左上角
int tile;               //L型骨牌的編號
//棋盤左上角的行號，列號，特殊方格所在的行號，列號，棋盤的大小
void chessbord(int tr, int tc, int dr, int dc, int size)
{
    int t, s;

    if(size == 1)
        return;
    s = size / 2;                          //分割棋盤
    t = tile++;                            //L型骨牌號

    //覆蓋左上角子棋盤
    if(dr<tr+s && dc<tc+s)
        chessbord(tr, tc, dr, dc, s);                //特殊方格在此棋盤中
    else
    {
        //此棋盤中無特殊方格，用t號L型骨牌覆蓋右下角
        board[tr+s-1][tc+s-1] = t;
        //覆蓋其餘方格
        chessbord(tr, tc, tr+s-1, tc+s-1, s);
    }

    if(dr<tr+s && dc>=tc+s)
        chessbord(tr, tc+s, dr, dc, s);
    else
    {
        //此棋盤中無特殊方格，用t號L型骨牌覆蓋左下角
        board[tr+s-1][tc+s] = t;
        chessbord(tr, tc+s, tr+s-1, tc+s, s);
    }

    if(dr>=tr+s && dc<tc+s)
        chessbord(tr+s, tc, dr, dc, s);
    else
    {
        //此棋盤中無特殊方格，用t號L型骨牌覆蓋右上角
        board[tr+s][tc+s-1] = t;
        chessbord(tr+s, tc, tr+s, tc+s-1, s);
    }

    if(dr>=tr+s && dc>=tc+s)
        chessbord(tr+s, tc+s, dr, dc, s);
    else
    {
        //此棋盤中無特殊方格，用t號L型骨牌覆蓋左上角
        board[tr+s][tc+s] = t;
        chessbord(tr+s, tc+s, tr+s, tc+s, s);
    }
}
 

複雜度分析：

T(k) = 

O(1)                          k=0

4T(k-1) + O(1)          k>0

     漸進意義上的最佳演算法

推導過程:  原式等價於  T(k)=4T(k-1)+1

遞推得: 4T(k-1)=4(4T(k-2)+1)=42T(k-2)+4    

T(k)= 42T(k-2)+4 +1

又有: 42T(k-2)=43T(k-3)+42

故 T(k)= 43T(k-3)+42+4+1

 ………………….

T(k)=4kT(0)+4k-1+…+4+1=O(4k)