將正整數n表示成一系列正整數之和。

n=n1+n2+...+nk;

其中n1>=n2>...>=nk>=1, k>=1

正整數n這種表示稱為正整數n的劃分。問題是求正整數n的不同劃分個數。

例如正整數6有如下11種不同的劃分

6；

5+1；

4+2，4+1+1；

3+3，3+2+1，3+1+1+1；

2+2+2，2+2+1+1，2+1+1+1+1；

1+1+1+1+1+1

輸入：正整數n。

輸出：n的不同劃分個數。

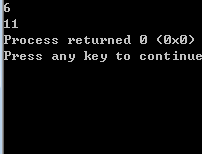
執行結果：

分析：前面的幾個例子中，問題本身都具有比較明顯的遞迴關係，易用遞迴函式直接求解。

本例若設p(n)為正整數n的劃分數，則難以找到遞迴關係

現考慮增加一個自變數，將最大加數n1不大於m的劃分個數記做q(n,m).q(n,m)有如下遞迴關係。

(1) q(n,1) = 1 n>=1

當最大加數n1 不大於1時，任何正整數n只有一種劃分形式，即

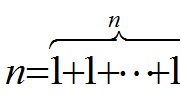
(2)q(n,m) = q(n,n), m>=n

最大加數n1 實際上不能大於n。因此，q(1,m) = 1.

(3)q(n,n) = 1 + q(n,n-1); n=m

正整數n的劃分由n1=n的劃分和n1<=n-1的劃分組成。

(4)q(n,m) = q(n,m-1) + q(n-m,m), n > m > 1;

正整數n的最大加數n1,不大於m的劃分，由n1 <= m-1的劃分和n1=m的劃分組成。

注意，正整數n的n1=m的所有劃分形式為

m+m1+…+mi =n    where mj ≤ m, j=1,2,…,i

That is, m1+…+mi =n-m

因此，n的n1=m的劃分個數是q(n-m, m)

所以，q(n,m)的遞迴關係：

q(n,m) =

1                                n=1, m=1

q(n,n)                         n<m

1 + q(n,n-1)                n=m

q(n,m-1) + q(n-m,m)   n>m>1

正整數n的劃分數p(n) = q(n,n)

int q(int n, int m)
{
    if(n<1 || m<1)        //小於1說明不存在
        return 0;
    if(n==1 || m==1)      //只有一種劃分形式
        return 1;
    if(m > n)             //最大加數m實際上不能大於n 因此q(1,m) = 1
        return q(n, n);
    if(n == m)            //正整數的劃分由n1=n的劃分和n1<=n-1的劃分組成
        return q(n, m-1) + 1;
    return q(n, m-1) + q(n-m, m);    //由n1=m的劃分和n1<=m-1的劃分組成
}