一、         密碼背景

基於有限域上離散對數問題的公鑰密碼體制，最著名的是ElGamal體制，是由T. ElGamal在1985年提出的 ElGamal有較好的安全性，同一明文在不同時刻會產生不同的密文應用廣泛，尤其數字簽名方面的應用，著明的美國數字簽名標準DSS就是ElGamal的一種變形。

二、         加解密演算法

加密過程：

(1)   A將明文訊息編碼成一個數m<p,並在橢圓群(a,b)中選擇一點

(2)   在區間[1,n-1]內，A選取一個隨機數k，計算點P1：P1=(x1,y1)=Kg;

(3)   依據接收方B的公鑰，A計算點=(x2,y2)=k;

(4)  A計算密文C=m

(5)  A傳送加密資料{Kg,,C}給接收方B；

解密過程：

(1)   接受方B收到加密資料={Kg,,C};

(2)   接受方B使用自己的私鑰作如下計算：

(3)   B計算m=(C-)/x，得明文m。

三、         橢圓曲線公鑰密碼演算法數論基礎

中學的時候我們學過圓錐曲線，比如橢圓、雙曲線和拋物線。因為描述這些曲線的方程都是二次方程，圓錐曲線又被稱為二次曲線。而橢圓曲線是則是由三次方程描述的一些曲線。更準確地說，橢圓曲線是由下面的方程描述的曲線：

y2=x3+ax+b其中4a3+27b2≠0

需要注意的是，橢圓曲線之所以叫“橢圓曲線”，是因為其曲線方程跟利用微積分計算橢圓周長的公式相似。實際上它的影象跟橢圓完全不搭邊。

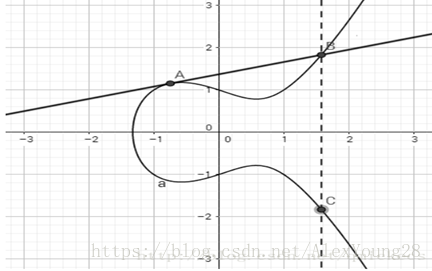
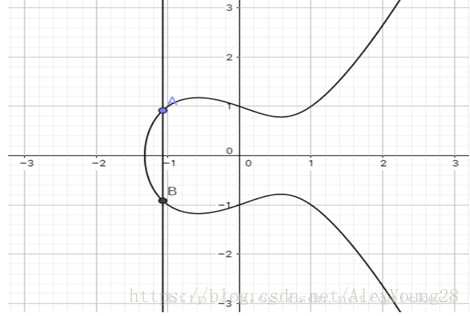
下圖是橢圓曲線y2=x3−x+1的影象

橢圓曲線有這樣的兩個性質：

關於X軸對稱

畫一條直線跟橢圓曲線相交，它們最多有三個交點

  橢圓曲線上的運算：

  由於橢圓曲線加密進行的運算實際上都是在橢圓曲線上進行的，所以接下來需要定義一些橢圓曲線上的運算。

必須注意的是，這裡把這些運算稱為“加法”和“乘法”僅僅是方便描述，他們跟平時認知的加法和乘法完全是兩碼事，完全可以給他們取其它名字（比如”乘法“和”冪運算“等）。

首先定義座標系中距離X軸無窮遠點為橢圓曲線上的一個特殊點，稱為0點。

那麼此時上述第二條性質可以加強為：過曲線上任意兩點（可重合）的直線必定與曲線相交於第三點。

然後定義橢圓曲線上點的加法。設橢圓曲線上有兩點，A和B點，那麼作過這兩點的直線與該曲線相交於第三點（C點），然後關於X軸對稱得到D點，則D為這兩個點的和，記作D=A+B。很明顯，D點也在該曲線上。所以橢圓曲線上兩點之和也是曲線上的點。

特別地，如果兩點重合，則作橢圓曲線在A點處的切線，與曲線相交於第二點（B點），然後關於X軸對稱得到C點，則C點為A點與自身的和，記作C=A+A

那麼關於這個加法，我們可以得到以下結論：

A+B=B+A

也就是橢圓曲線上的加法滿足交換律。

A+0=A

因為0點是無窮遠點，所以過A點與0點的直線是垂直於X軸的，它與曲線相交於另一點B點，那麼B點關於X軸對稱的點就是A點，即A點為A點和0點之和。

然後在加法的基礎上，定義橢圓曲線上點的乘法。

設P是橢圓曲線上的一個點，那麼正整數k乘以點P的結果由下面的式子定義，注意式子中的加法是上面提到的橢圓曲線上點的加法：

1∗P=P

2∗P=P+P

3∗P=2∗P+P

…

k∗P=(k−1)∗P+P

這個乘法滿足以下性質：

對於任意正整數k和j，有

k∗(j∗P)=(kj)∗P=(jk)∗P=j∗(k∗P)

橢圓曲線上的離散對數問題:

定義了基本的加法和乘法運算後，我們可以由此得到橢圓曲線加密依賴的數學難題。

k為正整數，P是橢圓曲線上的點（稱為基點），已知k∗P和P，計算k

從程式實現的角度來考慮，假設有這麼一個函式：

 Point add(Point A, Point B) {...}

函式引數是兩個橢圓曲線上的點，返回值是過兩個點的直線與橢圓曲線相交的第三個點關於X軸對稱的點。

那麼按照如下方式呼叫函式：

Point result =P;

for (int i = 0;i < k - 1; i++)

    result = add(P, result);

sendTo((result,P), others);

如果別人只知道result和P點，是很難求出k的值是多少的。

如果我們改一種記法，把橢圓曲線上點的加法記作乘法，原來的乘法就變成了冪運算，那麼上述難題的形式跟離散對數問題應該是一致的。即：

k為正整數，P是橢圓曲線上的點，已知Pk和P，計算k=logPPk。

所以這個難題叫橢圓曲線上的離散對數問題。

儘管兩者形式一致，但是他們並不等價。實際上這個問題比大整數質因子分解（RSA）和離散對數（DH）難題都要難得多，以致於同樣的安全強度下，橢圓曲線加密的金鑰比RSA和DH的短不少，這是橢圓曲線加密的一大優勢。

   有限域上的橢圓曲線:

   但是密碼學中，並不能使用上面介紹的實數域上的橢圓曲線。因為

1. 實數域上的橢圓曲線是連續的，有無限個點，密碼學要求有限點。

2. 實數域上的橢圓曲線的運算有誤差，不精確。密碼學要求精確。

所以我們需要引入有限域上的橢圓曲線。

所謂有限域上的橢圓曲線，簡單來說就是滿足下面式子要求的曲線（x, y, a, b都是小於素數p的非負整數）：

y2modp=x3+ax+bmodp其中4a3+27b2≠0modp

對比一下原先的橢圓曲線的方程：

y2=x3+ax+b其中4a3+27b2≠0

可以看到這個只是對原式進行了簡單的取模處理而已。實際上RSA和DH中也是基於這種形式的取模運算，它們其實也都是在有限域上進行的。

一、         密碼侷限性（攻擊方法）

橢圓曲線安全性依賴於基於橢圓曲線的有限群上的離散對數難題。於基於RSA的數字簽名和基於有限域離散對數的數字簽名相比，在相同的安全強度條件下，橢圓曲線方案有如下特點：簽名長度短，金鑰儲存空間小，特別適用於儲存空間有限、頻寬受限、要求高速實現的場合（如在智慧卡中應用）。

為使得有較好的安全性，這些引數的選取應滿足如下條件：

(1)   P越大越安全，但越大，計算速度就越慢，160位可以滿足目前的安全要求；

(2)   為了防止Pohlig-Hellman方法攻擊，n為大於素數（n>）,對於固定的有限域GF(P)，n應當儘可能大；

(3)   因為+ax+b無重複因子才可基於橢圓曲線(a,b)定義群，所以要求4+27(mod p)；

(4)  為了防止小步——大步攻擊，要保證P的階n足夠大，要求n4;

(5)   為了防止MOV規範法和Smart法，不能選取超奇異橢圓曲線和異常橢圓曲線等兩類特殊的曲線。