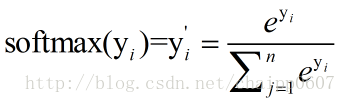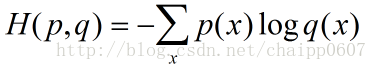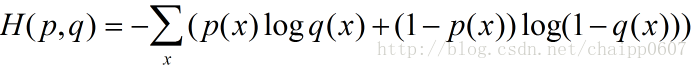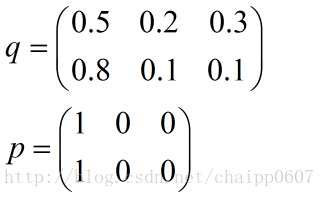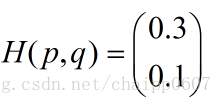一、交叉熵損失原理

一般情況下，在分類任務中，神經網路最後一個輸出層的節點個數與分類任務的標籤數相等。

假設最後的節點數為N，那麼對於每一個樣例，神經網路可以得到一個N維的陣列作為輸出結果，陣列中每一個維度會對應一個類別。在最理想的情況下，如果一個樣本屬於k，那麼這個類別所對應的第k個輸出節點的輸出值應該為1，而其他節點的輸出都為0，即[0,0,1,0,….0,0]，這個陣列也就是樣本的Label，是神經網路最期望的輸出結果，交叉熵就是用來判定實際的輸出與期望的輸出的接近程度。

二、公式

1.softmax迴歸

假設神經網路的原始輸出為y1,y2,….,yn，那麼經過Softmax迴歸處理之後的輸出為：

單個節點的輸出變成的一個概率值。

2.交叉熵的原理

交叉熵刻畫的是實際輸出（概率）與期望輸出（概率）的距離，也就是交叉熵的值越小，兩個概率分佈就越接近。假設概率分佈p為期望輸出，概率分佈q為實際輸出，H(p,q)為交叉熵，則：

除此之外，交叉熵還有另一種表達形式，還是使用上面的假設條件：

在實際的使用訓練過程中，資料往往是組合成為一個batch來使用，所以對用的神經網路的輸出應該是一個m*n的二維矩陣，其中m為batch的個數，n為分類數目，而對應的Label也是一個二維矩陣，還是拿上面的資料，組合成一個batch=2的矩陣：

所以交叉熵的結果應該是一個列向量（根據第一種方法）： 

而對於一個batch，最後取平均為0.2。

三、Tensorflow實現

函式定義：def softmax_cross_entropy_with_logits(_sentinel=None, labels=None, logits=None, dim=-1, name=None)

示例：計算batch = 2,num_labels = 3的2*3矩陣

實際輸出（概率）：

[[0.2,0.1,0.9],

[0.3,0.4,0.6]]

期望輸出（概率）

[[0,0,1],

[1,0,0]]

計算交叉熵損失，對於一個batch，最後取平均為1.36573195。

import tensorflow as tf

input_data = tf.Variable([[0.2, 0.1, 0.9], [0.3, 0.4, 0.6]], dtype=tf.float32)
output = tf.nn.softmax_cross_entropy_with_logits(logits=input_data, labels=[[0, 0, 1], [1, 0, 0]])
with tf.Session() as sess:
    init = tf.global_variables_initializer()
    sess.run(init)
    print(sess.run(output))
    # [1.36573195]