暫無連結

鍛造

題目背景

勇者雖然武力值很高，但在經歷了多次戰鬥後，發現怪物越來越難打，於是開始思考是不是自己平時鍛鍊沒到位，於是苦練一個月後發現……自己連一個史萊姆都打不過了。
勇者的精靈路由器告訴勇者其實是他自己的武器不好，並把他指引到了鍛造廠。

題目描述

“歡迎啊，老朋友。”
一陣寒暄過後，廠長帶他們參觀了廠子四周，並給他們講鍛造的流程。
“我們這裡的武器分成若干的等級，等級越高武器就越厲害，並且對每一等級的武器都有兩種屬性值 $b$

b 和 $c$，但是我們初始只能花 $a$個金幣來生產 $1$

1 把 $0$級劍……”
“所以你們廠子怎麼這麼垃圾啊，不能一下子就造出來 $999$級的武器嗎？”勇者不耐煩的打斷了廠長的話。
“彆著急，還沒開始講鍛造呢……那我們舉例你手中有一把 $x$

x 級武器和一把 $y$級武器 $(y = max(x − 1, 0))$，我們令鍛造附加值 $k = min(c_x, b_y)$，則
你有 $\frac{k}{c_x}$的概率將兩把武器融合成一把 $x + 1$級的武器。”
“……但是，鍛造不是一帆風順的，你同樣有 $1 −\frac{k}{c_x}$的概率將兩把武器融合成一把 $max(x − 1, 0)$級的武器……”
勇者聽完後暗暗思忖，他知道廠長一定又想借此機會坑騙他的零花錢，於是求助這個村最聰明的智者——你，來告訴他，想要強化出一把 $n$級的武器，其期望花費為多少？
由於勇者不精通高精度小數，所以你只需要將答案對 $998244353(7 ×17 × 2^{23} + 1$，一個質數 ) 取模即可。

格式

輸入格式

第一行兩個整數 $n, a$，含義如題所示。
為了避免輸入量過大，第二行五個整數 $b_x, b_y, c_x, c_y, p$，按照下列程式碼
來生成 $b$和 $c$陣列。

b[0]=by+1;c[0]=cy+1;
for(int i=1;i<n;i++){
b[i]=((long long)b[i-1]*bx+by)%p+1;
c[i]=((long long)c[i-1]*cx+cy)%p+1;
}

輸出格式

輸出一行一個整數，表示期望花費。

樣例

樣例 1 輸入

0 6432
4602677 3944535 2618884 6368297 9477531

樣例 1 輸出

6432

樣例 2 輸入

1 3639650
6136976 5520115 2835750 9072363 9302097

樣例 2 輸出

150643649

樣例 3 輸入

10 2
2 33 6 66 2333333

樣例 3 輸出

976750710
3

樣例 4 輸入

200 5708788
0 0 0 0 1

樣例 4 輸出

696441597

資料範圍

對於特殊性質處標示為“有”的資料滿足 $p = 1$。
對於 $100\%$的資料， $0 ≤ a ≤ 10^7, 0 ≤ b_x, b_y, c_x, c_y < p < 10^7, 0 ≤ n ≤10^7$

題解

乍一看以為 $p=1$的時候成功率 $100\%$，感覺 $60$分穩了，然而定睛一看：特麼 $dp[1]$怎麼算？？？

還是隻能老老實實推期望，先畫個圖：

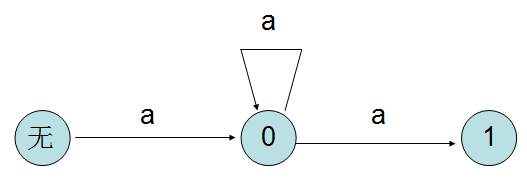
設 $f[i]$為有了一把 $i$級劍，要得到一把 $1$級劍的期望花費，從 $0$級升到 $1$級的概率為 $p$，根據上圖，可以列出方程組如下：
$\left\{ \begin{aligned} &f[1]=0\\ &f[0]=(1-p)\times f[0]+p\times f[1] \end{aligned} \right.$

解得 $f[0]=a\times \frac{1-p}{p}$，算出 $dp[1]=f[0]+a=\frac{a}{p}$。

現在我們有了 $60$分，考慮如何遞推下去，當我們融合一把 $i-1$和 $i-2$級的劍時，如果失敗了，會得到一把 $i-2$的劍，所以對於一次融合操作，失敗時消耗的實際上是一把 $i-1$級的劍，又因為我們的期望融合次數為 $\frac{1}{p}$，最終可以得到鍛造一把 $i$級劍的期望花費的遞推式：
$dp[i]=dp[i-1]\times \frac{1}{p}+dp[i-2]$