關聯文章:

  上一篇博文中，我們詳細地分析了樹的基本概念以及二叉查詢樹的實現過程，基於二叉查詢樹的特性，即對於樹種的每個結點T（T可能是父結點）,它的左子樹中所有項的值小T中的值，而它的右子樹中所有項的值都大於T中的值。這意味著該樹所有的元素可以用某種規則進行排序(取決於Comparable介面的實現)，以致於二叉樹查詢樹能夠勝任快速地查詢過程，這個查詢的過程的時間複雜度為O(logN)，但是這個時間複雜度並不是嚴格意義上的O(logN)，在某些情況下還是會上升到O(N)，顯然這並不是一件好事情，因此本篇我們將來討論另一種更為穩定的二叉樹，它就是AVL樹。以上是本篇將會討論的主要內容：

普通二叉查詢樹的問題

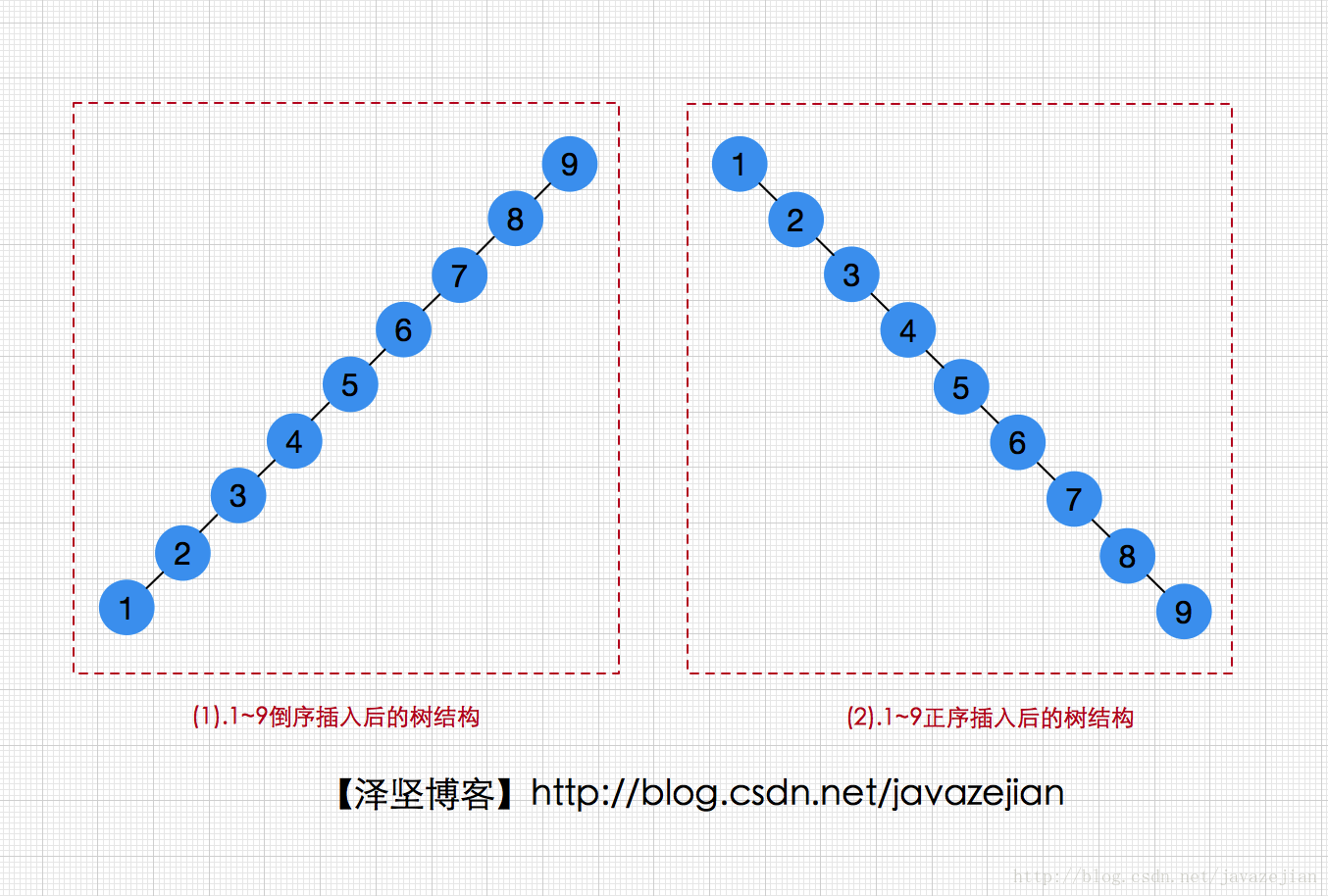
  在開篇，我們提到過，普通二叉樹（二叉查詢樹）在操作的時間複雜度上不一定遵循O(㏒n)，也有可能是O(n)，這是為什麼呢？在上一篇中，我們明明插入都按照一定規則比較的呀，其實那是因為我們在上篇測試時執行了隨機插入的操作，如果此時利用上篇實現的二叉搜尋樹將一段已排序好的資料一個個插入後，就會發現如下情況了：

  從圖中我們可以發現，把已排序的1-9資料進行正序和倒序插入後，樹的結構已變成單向左子樹或者右子樹了，如果我們在往裡插入已排序的資料，那麼單向左子樹或者右子樹越來越長，此時已跟單鏈表沒有什麼區別了，因此對此結構的操作時間複雜度自然就由O(㏒n)變成O(n)了，這也就是普通二叉查詢樹不是嚴格意義上O(㏒n)的原因。那麼該如何解決這個問題呢？事實上一種解決的辦法就是要有一個稱為平衡的附加結構條件即：任何結點的深度不得過深，而這種資料結構就是我們本篇要分析的平衡二叉樹（AVL），它本身也是一種二叉查詢樹，只不過不會出現前面我們分析的情形罷了，接下來我們就來分析一下這棵平衡二叉樹。

平衡二叉樹的定義

  通過上面的分析，我們明白的普通二叉查詢樹的不足，也知道了如何去解決這個缺點，即構建樹時要求任何結點的深度不得過深（子樹高度相差不超過1），而最終這棵樹就是平衡二叉樹（Balanced Binary Tree），它是G.M. Adelson-Velsky 和 E.M. Landis在1962年在論文中發表的，因此又叫AVL樹。這裡我們還需要明確一個概念，AVL樹只是實現平衡二叉樹的一種方法，它還有很多的其他實現方法如紅黑樹、替罪羊樹、Treap、伸展樹等，後面我們還會分析其他樹的實現。ok~，接著來了解一下AVL樹的特性：一棵AVL樹是其每個結點的左子樹和右子樹的高度最多相差1的二叉查詢樹(空樹的高度為-1)，這個差值也稱為平衡因子

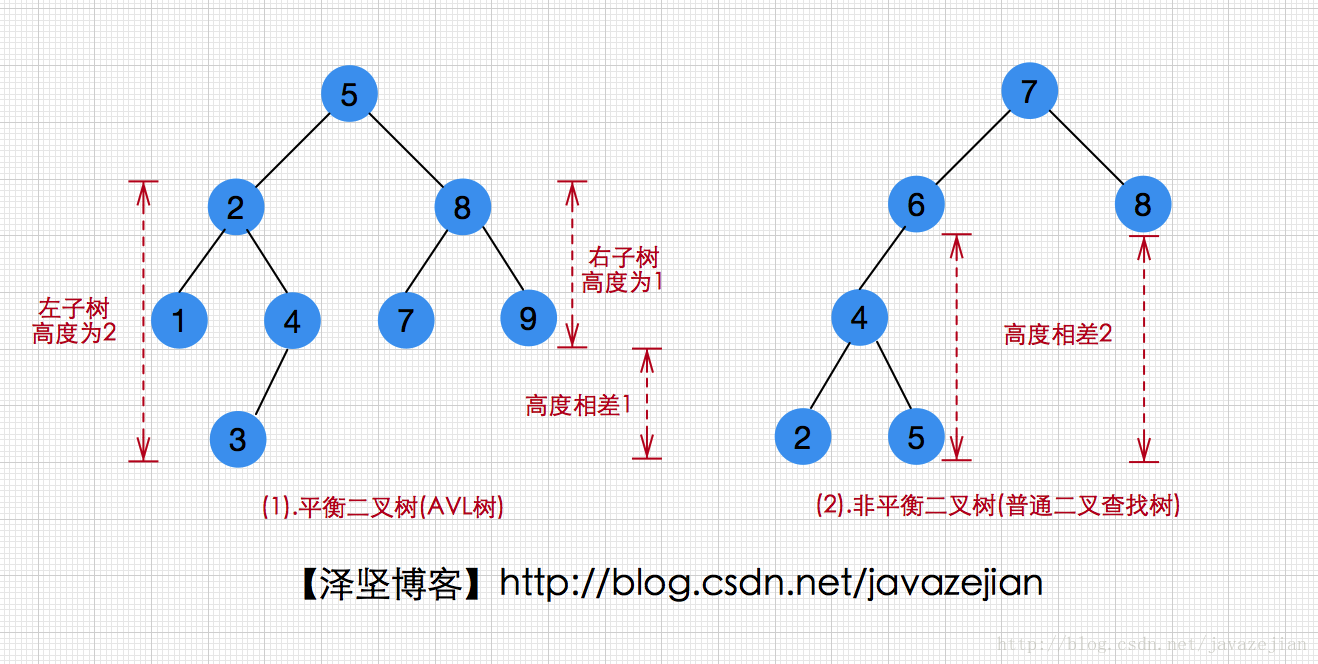
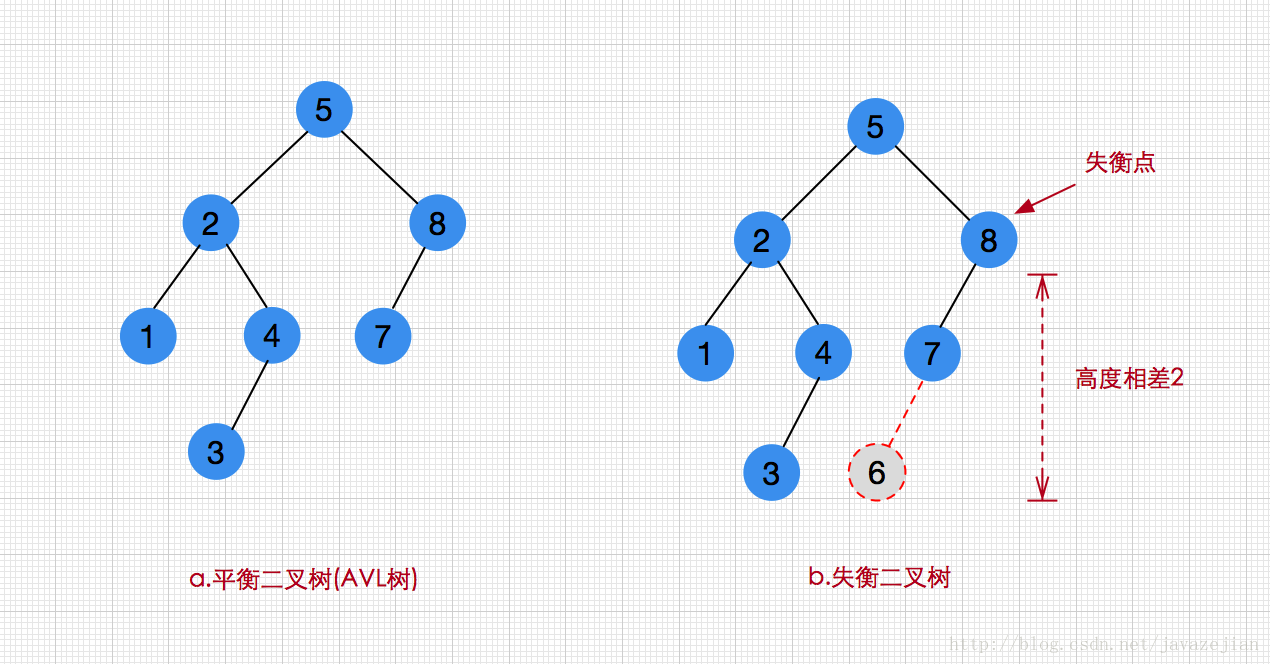
  圖(1)顯然就是一棵平衡二叉樹，它每個結點的左子樹和右子樹的高度最多相差1，同時也是一棵二叉查詢樹，而圖二雖然也是一棵二叉查詢樹，但是它每個結點的左子樹和右子樹的高度相差卻到達了2，因此不是平衡二叉樹。理解了平衡二叉樹的概念後，我們在思考一下，那些操作可能引起平衡發生變化呢？顯然只有那些引起結點數量變化的操作才可能導致平衡被改變，也就是刪除和插入操作了，如下圖，我們把6插入到圖a後，結構變成了圖b，這時原本的平衡二叉樹就失去平衡了。

  顯然圖b已失去平衡，如果發生這樣的情況，我們就必須考慮插入元素後恢復二叉樹的平衡性質，實際上也總是可以通過對樹進行簡單的修復來讓其重新恢復到平衡，而這樣的簡單操作我們就稱之為旋轉，當然旋轉也有單旋轉和雙旋轉之分，下面我們將會一一分析，這裡有點需要明白的是，無論是插入還是刪除，只有那些從插入或者刪除點到根結點的路徑上的結點的平衡才有可能被改變，因為只有這些結點的子樹才可能發生變化，所以最終也只需針對這些點進行平衡修復操作即可。

平衡二叉樹的設計與實現

  ok~，有了旋轉的概念後，我們接著瞭解如何通過旋轉來修復一棵失衡的二叉樹，這裡假設結點X是失衡點，它必須重新恢復平衡，由於任意結點的孩子結點最多有兩個，而且導致失衡的必要條件是X結點的兩棵子樹高度差為2(大於1)，因此一般只有以下4種情況可能導致X點失去平衡：
① 在結點X的左孩子結點的左子樹中插入元素
② 在結點X的左孩子結點的右子樹中插入元素
③ 在結點X的右孩子結點的左子樹中插入元素
④ 在結點X的右孩子結點的右子樹中插入元素
以上4種情況，其中第①情況和第④情況是對稱的，可以通過單旋轉來解決，而第②種情況和第③情況是對稱的，需要雙旋轉來解決。在分析這四種情況前，我們先看看AVL的結點該如何設計的，其宣告如下：

package com.zejian.structures.Tree.AVLTree;

/**
 * Created by zejian on 2016/12/25.
 * Blog : http://blog.csdn.net/javazejian [原文地址,請尊重原創]
 * 平衡二叉搜尋樹(AVL樹)節點
 */
public class AVLNode<T extends Comparable> {

    public AVLNode<T> left;//左結點

    public AVLNode<T> right;//右結點

    public T data;

    public int height;//當前結點的高度

    public AVLNode(T data) {
        this(null,null,data);
    }

    public AVLNode(AVLNode<T> left, AVLNode<T> right, T data) {
        this(left,right,data,0);
    }

    public AVLNode(AVLNode<T> left, AVLNode<T> right, T data, int height) {
        this.left=left;
        this.right=right;
        this.data=data;
        this.height = height;
    }
}

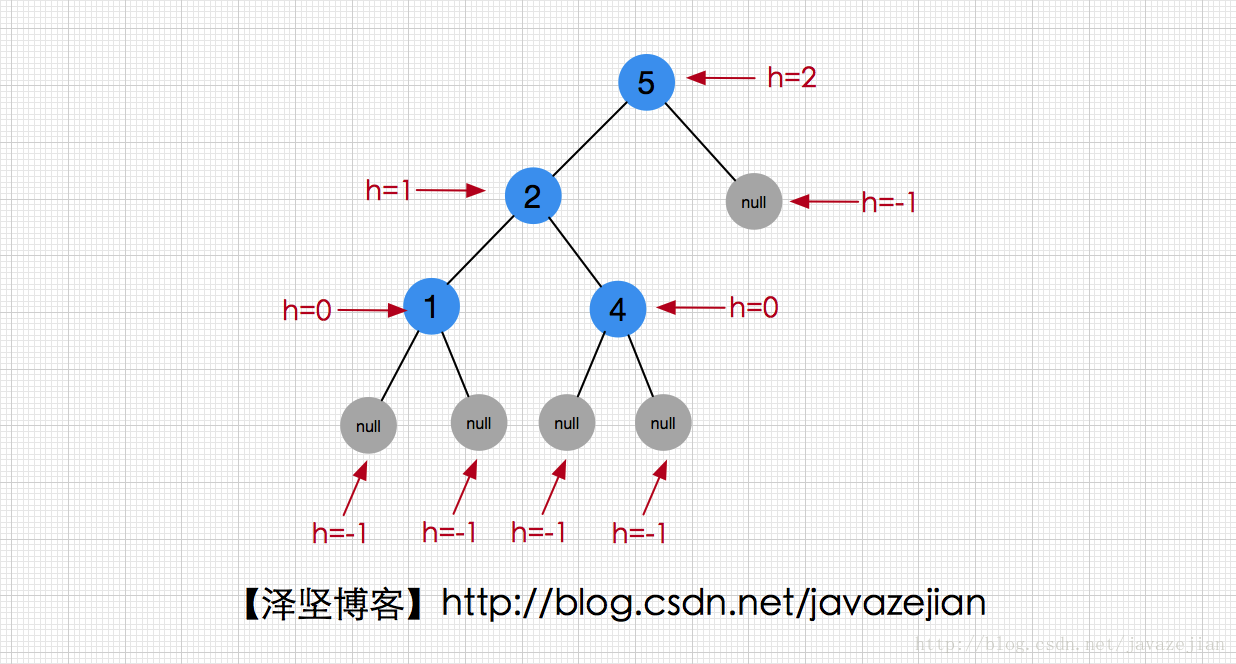
  可以看出，為了滿足平衡二叉樹的特性，需要在原來的二叉搜尋樹(BST)的結點中新增一個height的欄位表示高度，方便我們計算，這裡強調一下，高度和深度一組相反的概念，高度是指當前結點到葉子結點的最長路徑，如所有葉子結點的高度都為0，而深度則是指從根結點到當前結點的最大路徑，如根結點的深度為0。這裡約定空結點（空子樹）的高度為-1，葉子結點的高度為0，非葉子節點的高度則根據其子樹的高度而計算獲取，如下圖：

ok~，瞭解上述的內容，下面就來分析4種可能失衡的情景。

平衡二叉樹的單旋轉演算法與實現

左左單旋轉(LL)情景①分析

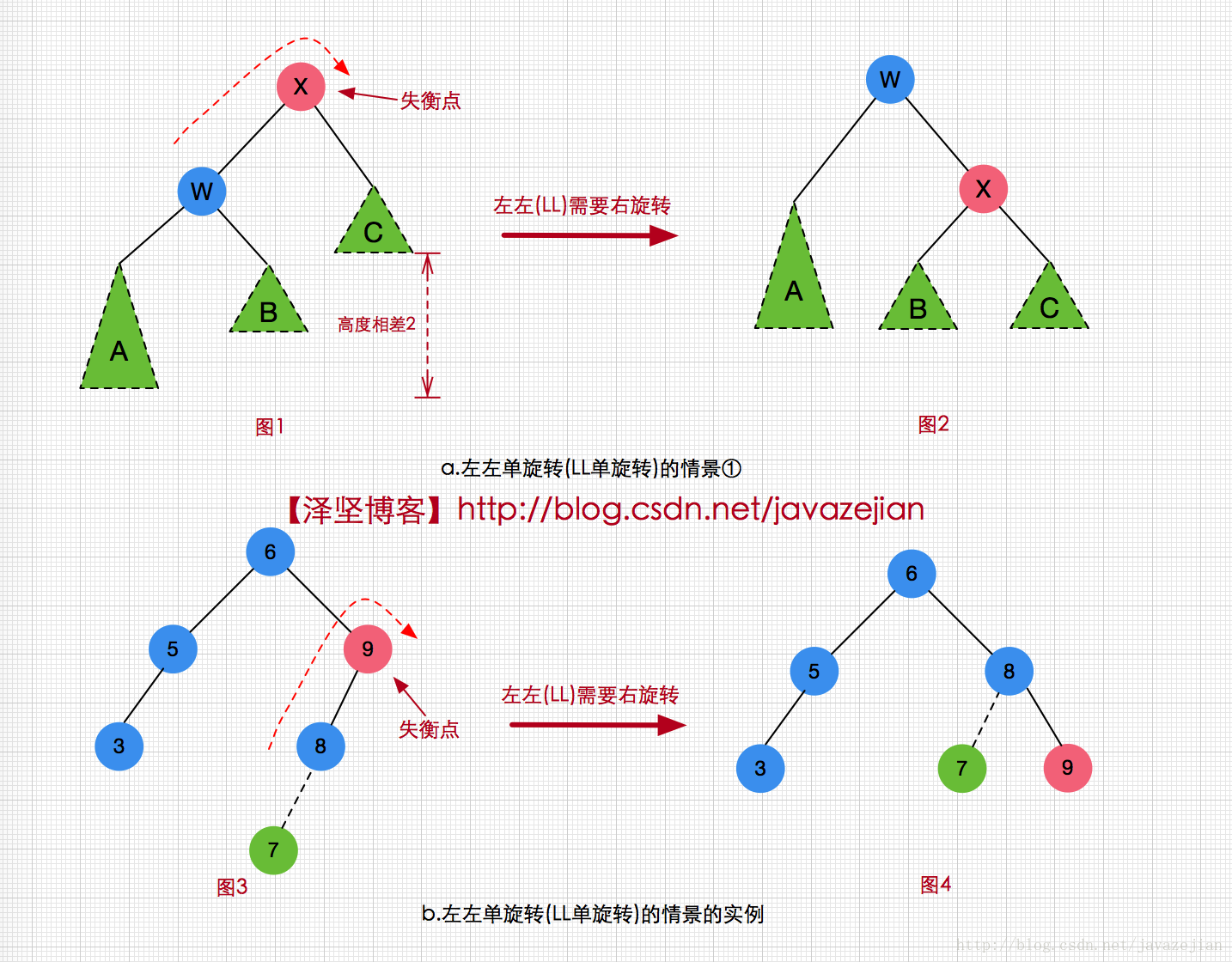
  從下圖可以看出，結點X並不能滿足AVL樹的性質，因為它的左子樹比右子樹深2層，這種情況就是典型的LL情景，此時需要通過右向旋轉來修復失衡的樹，如圖1，X經過右旋轉後變成圖2，W變為根結點，X變為W的右子樹，同時W的右子樹變為X的左子樹，樹又重新回到平衡，各個結點的子樹高度差都已在正常範圍。一般情況下，我們把X結點稱為失衡點，修復一棵被破壞的AVL樹時，找到失衡點是很重要的並把通過一次旋轉即可修復平衡的操作叫做單旋轉，從圖3和圖4可知，在原始AVL樹插入7結點後，結點9變為失衡點，樹再滿足AVL性質，因此需要對9結點進行左左單旋轉(即向右旋轉)後，得到圖4，我們發現此時並沒有操作樹的根結點(6)，實際上這是因為正常情況下，不必從樹的根結點進行旋轉，而是從插入結點處開始，向上遍歷樹，並更新和修復在這個路徑上的每個結點的平衡及其平衡資訊(高度)即可。

其程式碼實現如下，比較簡單：

/**
 * 左左單旋轉(LL旋轉) w變為x的根結點, x變為w的右子樹
 * @param x
 * @return
 */
private AVLNode<T> singleRotateLeft(AVLNode<T> x){
    //把w結點旋轉為根結點
    AVLNode<T> w=  x.left;
    //同時w的右子樹變為x的左子樹
    x.left=w.right;
    //x變為w的右子樹
    w.right=x;
    //重新計算x/w的高度
    x.height=Math.max(height(x.left),height(x.right))+1;
    w.height=Math.max(height(w.left),x.height)+1;
    return w;//返回新的根結點
}

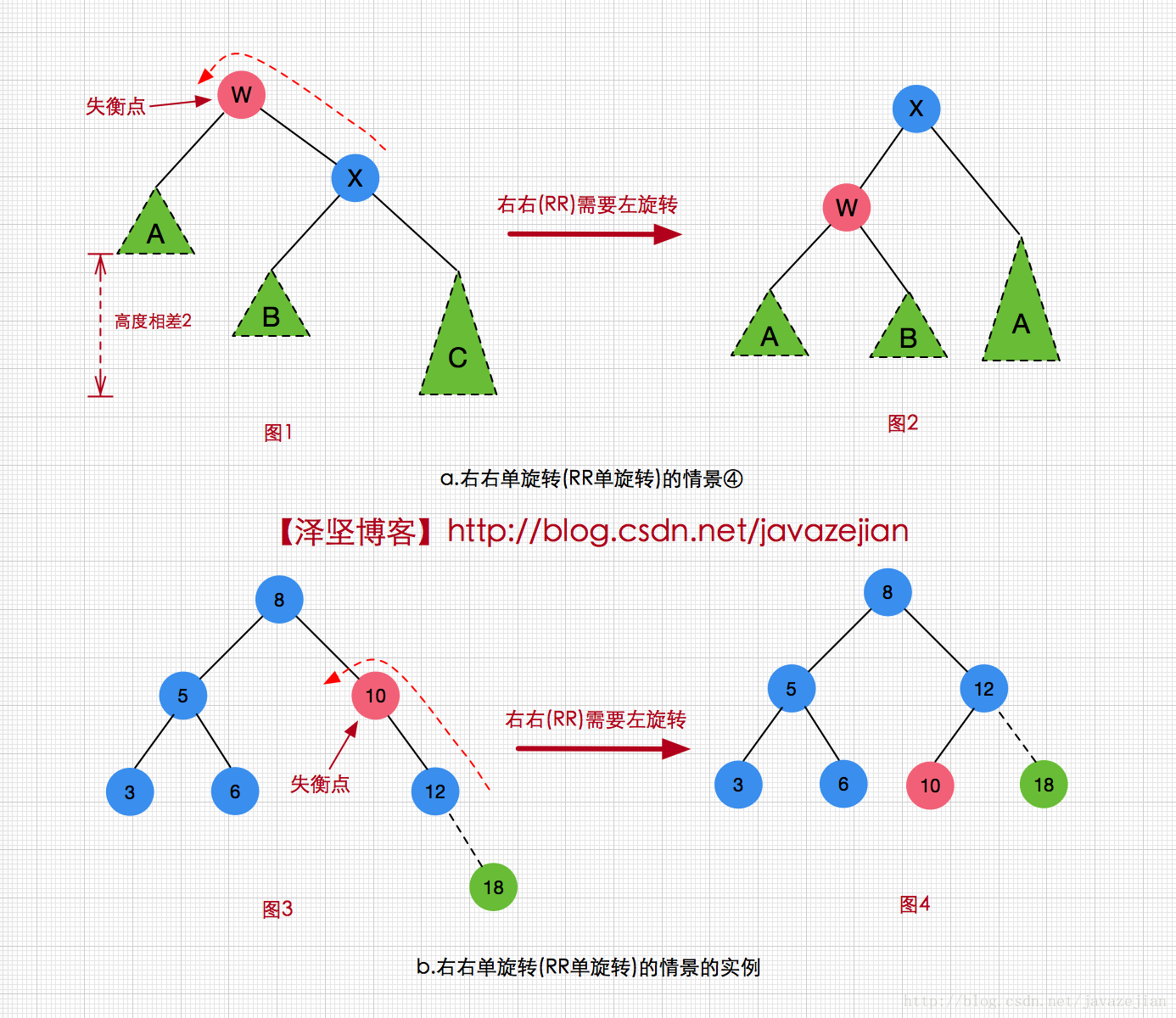
右右單旋轉(RR)情景④分析

  接著再來看看右右單旋轉(RR)的情景，如下圖，可以發現與左左單旋轉的情況恰好是一種映象關係，同樣結點X並不能滿足AVL樹的性質，在這樣的情景下，需要對X結點進行左旋轉來修復樹的平衡，如圖1經左旋轉後變了圖2，此時X變為了根結點，W變為X的左孩子，X的左子樹變為W的右子樹，而樹又重新恢復了平衡。如圖3和圖4的例項情景，原始的AVL樹在12處插入結點18後，結點10就變成了失衡點，因為10的左子樹和右子樹的高度相差2，顯然不符合AVL樹性質，需要對結點10進行右右單旋轉修復(向左旋轉)，然後得到圖4，此時樹重新回到了平衡，這便是右右單旋轉(RR)的修復情景。

程式碼實現如下：

/**
 * 右右單旋轉(RR旋轉) x變為w的根結點, w變為x的左子樹
 * @return
 */
private AVLNode<T> singleRotateRight(AVLNode<T> w){

    AVLNode<T> x=w.right;

    w.right=x.left;
    x.left=w;

    //重新計算x/w的高度
    w.height=Math.max(height(w.left),height(w.right))+1;
    x.height=Math.max(height(x.left),w.height)+1;

    //返回新的根結點
    return x;
}

平衡二叉樹的雙旋轉演算法與實現

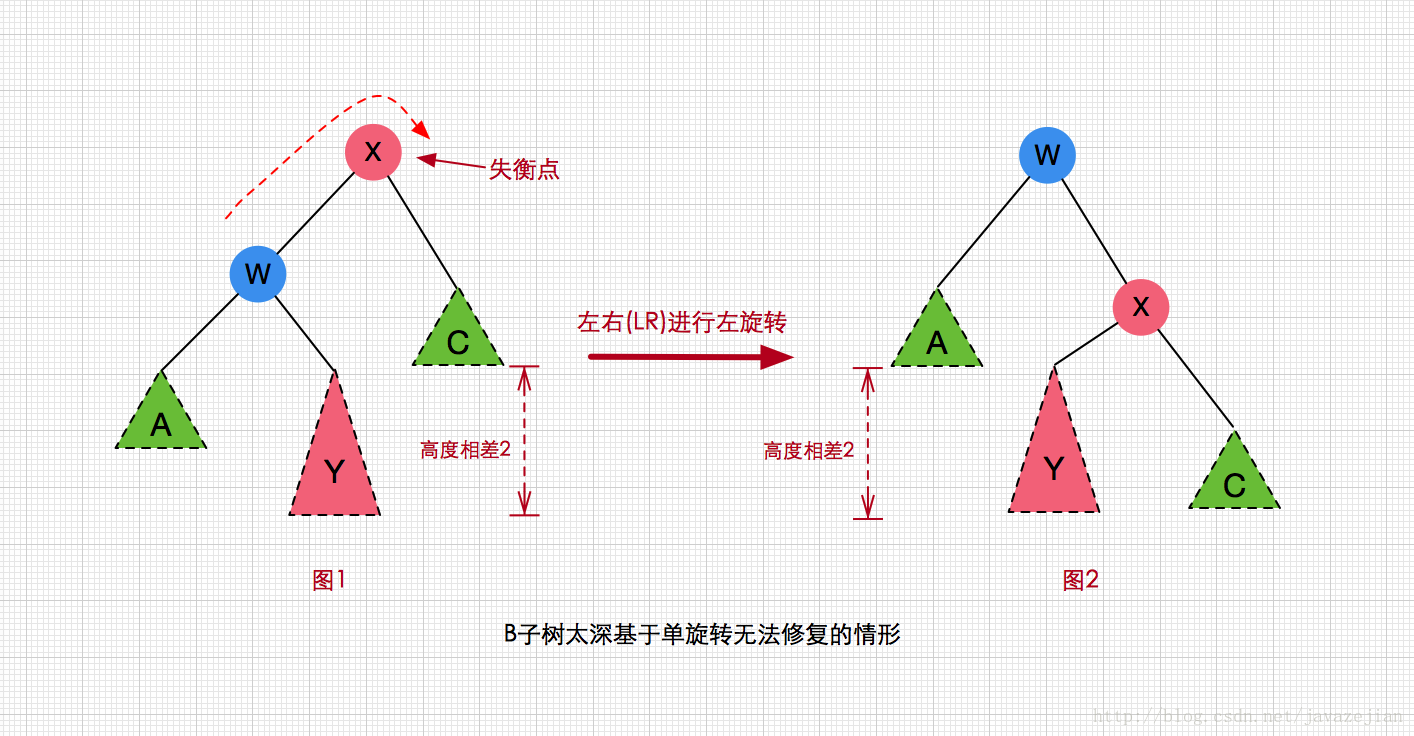
  前面兩種情景都已分析完，它們都是基於單旋轉的演算法，但這種演算法存在一個問題，那就是對情景②③無法生效，根本問題在於子樹Y太深了，如下圖所示：

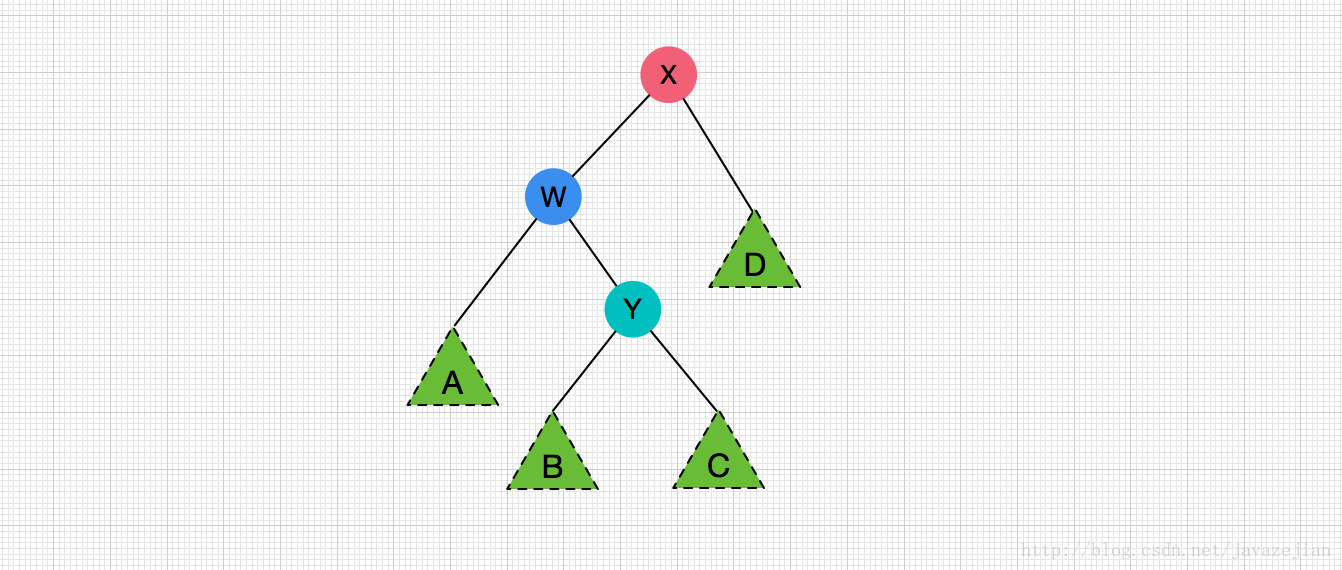
  顯然經過一次單旋轉的修復後無論是X或者W作為根結點都無法符合AVL樹的性質，此時就需要用雙旋轉演算法來實現了。由於子樹Y是在插入某個結點後導致X結點的左右子樹失去平衡，那麼就說明子樹Y肯定是非空的，因此為了易於理解，我們可以把子樹Y看作一個根結點和兩棵子樹，如下圖所示：

  ok~，明白了單旋轉對於情景②③的窘境，下面我們就通過雙旋轉演算法來解開這個窘境。

左右雙旋轉(LR)情景②分析

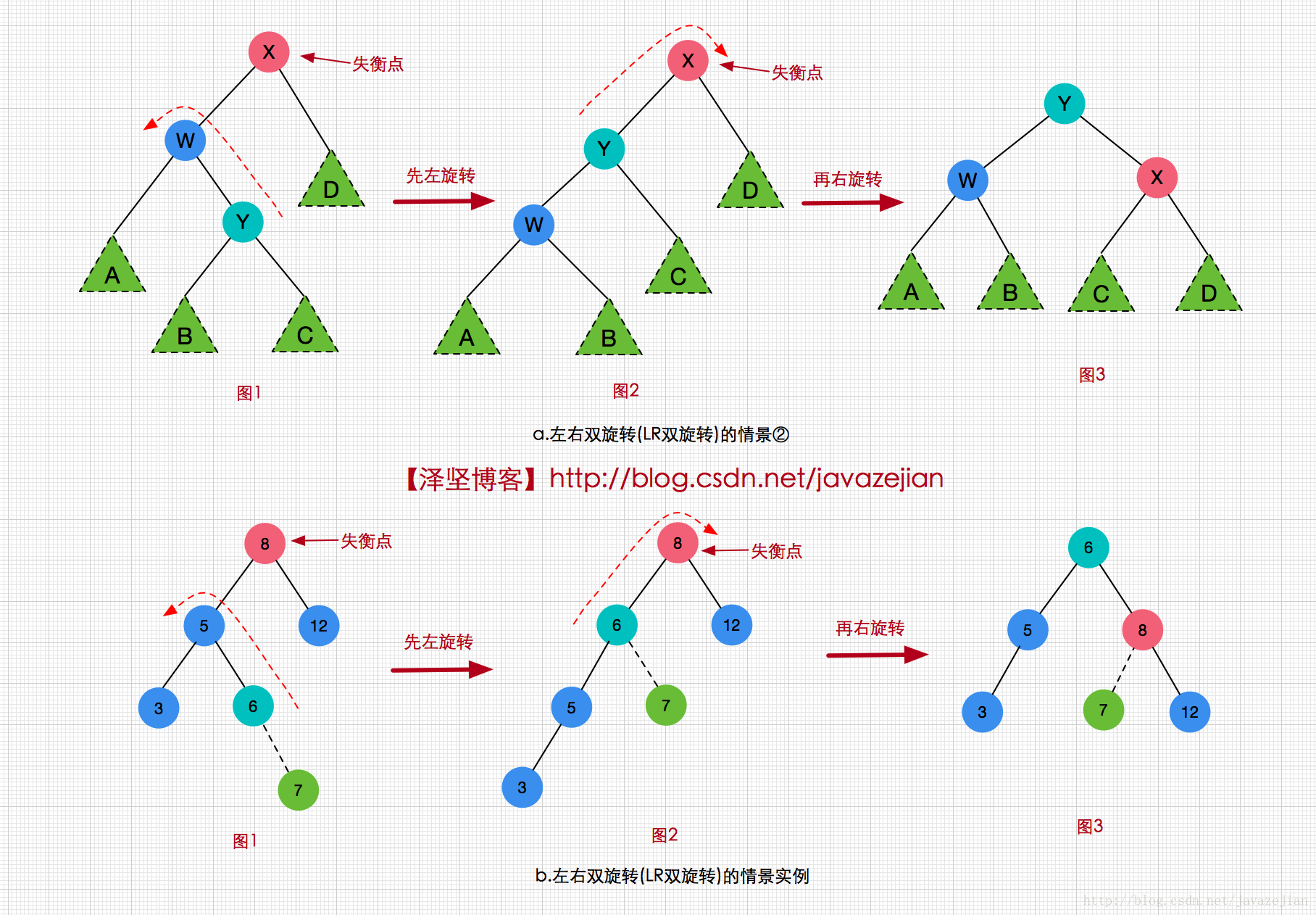
  為了重新平衡，通過上述的分析顯然不能把X根結點，而X與W間的旋轉也解決不了問題，那唯一的旋轉就是把Y作為新根。這樣的話，X、W就不得不成為Y的孩子結點，其中W作為Y的左孩子結點，而X成為Y的右孩子結點。這裡我們以下圖為例來分析，為了達到以上結果，需要W、Y進行單旋轉（圖1），這裡我們可把WY組成的子樹看成前面的右右旋轉情景，然後進行左向旋轉，得到圖2，W變為Y的左子樹同時Y的左子樹B變成W的右子樹，其他不變，到此第一次旋轉完成，進行第二次旋轉，以X結點向右進行旋轉(同樣可看作左左情景)，由圖2得到圖3，X變成Y的右孩子結點並且Y的右子樹C變成X的左子樹，第二次旋轉完成，樹也重新恢復到平衡。

  在左右雙旋轉例項圖123中，在原AVL樹種插入結點7後，結點8變成了失衡點，此時需要把6結點變為根結點才能重新恢復平衡。因此先進行左向旋轉再進行右向旋轉，最後樹恢復平衡。演算法程式碼實現如下：

/**
 * 左右旋轉(LR旋轉) x(根) w y 結點 把y變成根結點
 * @return
 */
private AVLNode<T> doubleRotateWithLeft(AVLNode<T> x){
    //w先進行RR旋轉
    x.left=singleRotateRight(x.left);
    //再進行x的LL旋轉
    return singleRotateLeft(x);
}

右左雙旋轉(RL)情景③分析

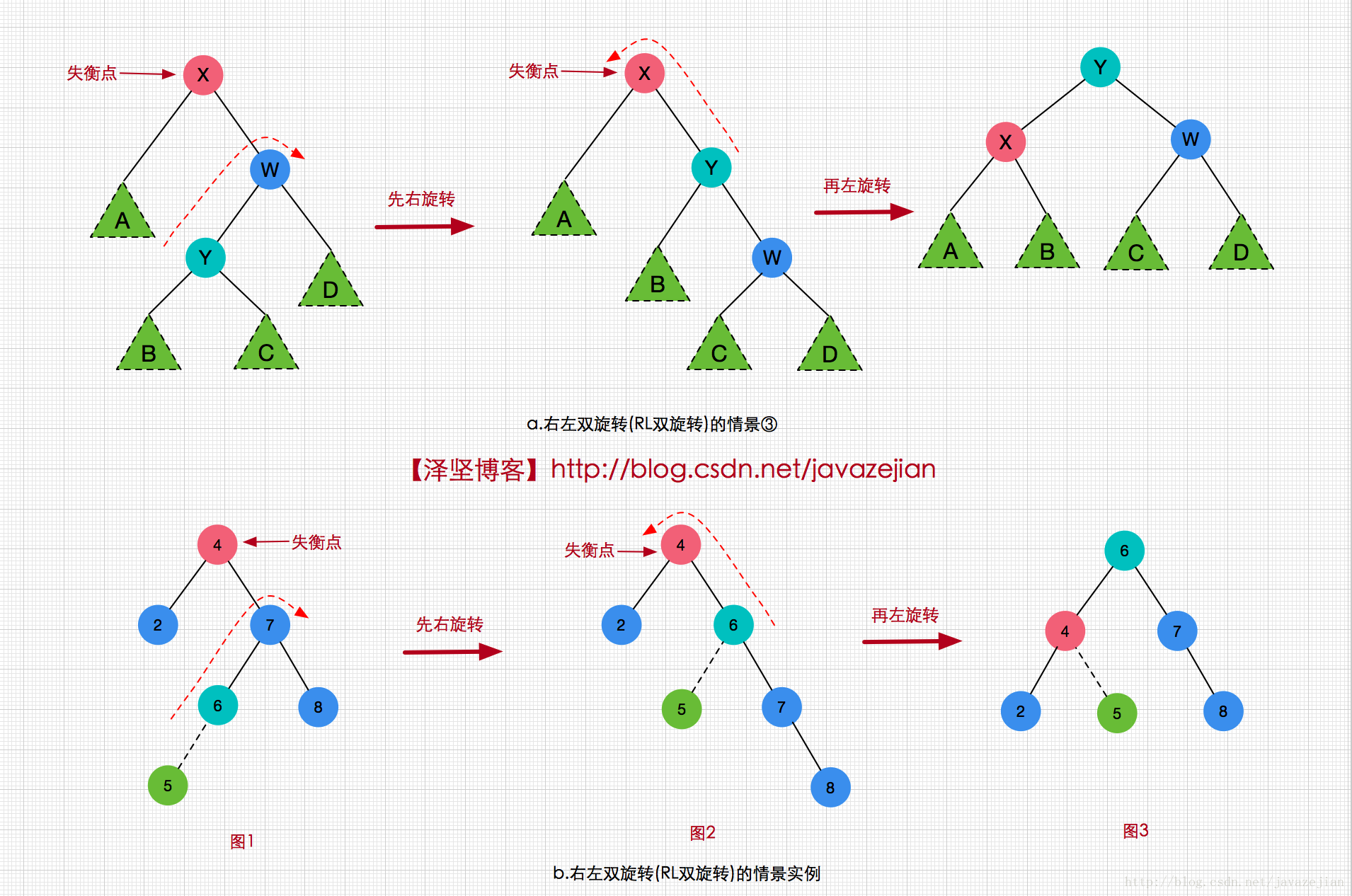
  對於右左雙旋轉(RL)情景和左右雙旋轉(LR)情景是一對映象，旋轉的原理上一樣的，這裡就不廢話了，給出下圖協助理解即可(已很清晰了)：

實現程式碼如下：

/**
 * 右左旋轉(RL旋轉)
 * @param w
 * @return
 */
private AVLNode<T> doubleRotateWithRight(AVLNode<T> x){
    //先進行LL旋轉
    x.right=singleRotateLeft(x.right);
    //再進行RR旋轉
    return singleRotateRight(x);
}

  好~，到此4種情況都已分析完畢，接著我們就利用這種四種情況來重寫AVL樹的插入操作過程。

平衡二叉樹插入操作的實現

  實際上，有了上述四種情況後，編寫插入操作的編碼細節並不會太困難，這裡我們給出主要思路和程式碼實現即可（很清晰的註釋），與BST（二叉查詢樹）的插入實現原理一樣，使用遞迴演算法，根據值大小查詢到插入位置，然後進行插入操作，插入完成後，我們需要進行平衡判斷，評估子樹是否需要進行平衡修復，需要則利用上述的四種情景套入程式碼即可，最後要記得重新計算插入結點路徑上的高度。程式碼實現如下：

/**
* 插入方法
* @param data
*/
@Override
public void insert(T data) {
   if (data==null){
       throw new RuntimeException("data can\'t not be null ");
   }
   this.root=insert(data,root);
}

private AVLNode<T> insert(T data , AVLNode<T> p){

   //說明已沒有孩子結點,可以建立新結點插入了.
   if(p==null){
       p=new AVLNode<T>(data);
   }else if(data.compareTo(p.data)<0){//向左子樹尋找插入位置
       p.left=insert(data,p.left);

       //插入後計運算元樹的高度,等於2則需要重新恢復平衡,由於是左邊插入,左子樹的高度肯定大於等於右子樹的高度
       if(height(p.left)-height(p.right)==2){
           //判斷data是插入點的左孩子還是右孩子
           if(data.compareTo(p.left.data)<0){
               //進行LL旋轉
               p=singleRotateLeft(p);
           }else {
               //進行左右旋轉
               p=doubleRotateWithLeft(p);
           }
       }
   }else if (data.compareTo(p.data)>0){//向右子樹尋找插入位置
       p.right=insert(data,p.right);

       if(height(p.right)-height(p.left)==2){
           if (data.compareTo(p.right.data)<0){
               //進行右左旋轉
               p=doubleRotateWithRight(p);
           }else {
               p=singleRotateRight(p);
           }
       }
   }
   else
    ;//if exist do nothing
   //重新計算各個結點的高度
   p.height = Math.max( height( p.left ), height( p.right ) ) + 1;

   return p;//返回根結點
}

平衡二叉樹刪除操作的實現

  關於平衡二叉樹的刪除，我們這裡給出一種遞迴的實現方案，和二叉查詢樹中刪除方法的實現類似，但是在移除結點後需要進行平衡檢測，以便判斷是否需要進行平衡修復，主要明白的是，這種實現方式在刪除時效率並不高，不過我們並不打算過多討論它，更復雜的刪除操作過程將放在紅黑樹中進行討論。下面給出實現程式碼：

/**
 * 刪除方法
 * @param data
 */
@Override
public void remove(T data) {
    if (data==null){
        throw new RuntimeException("data can\'t not be null ");
    }
    this.root=remove(data,root);
}

/**
 * 刪除操作
 * @param data
 * @param p
 * @return
 */
private AVLNode<T> remove(T data,AVLNode<T> p){

    if(p ==null)
        return null;

    int result=data.compareTo(p.data);

    //從左子樹查詢需要刪除的元素
    if(result<0){
        p.left=remove(data,p.left);

        //檢測是否平衡
        if(height(p.right)-height(p.left)==2){
            AVLNode<T> currentNode=p.right;
            //判斷需要那種旋轉
            if(height(currentNode.left)>height(currentNode.right)){
                //LL
                p=singleRotateLeft(p);
            }else{
                //LR
                p=doubleRotateWithLeft(p);
            }
        }

    }
    //從右子樹查詢需要刪除的元素
    else if(result>0){
        p.right=remove(data,p.right);
        //檢測是否平衡
        if(height(p.left)-height(p.right)==2){
            AVLNode<T> currentNode=p.left;
            //判斷需要那種旋轉
            if(height(currentNode.right)>height(currentNode.left)){
                //RR
                p=singleRotateRight(p);
            }else{
                //RL
                p=doubleRotateWithRight(p);
            }
        }
    }
    //已找到需要刪除的元素,並且要刪除的結點擁有兩個子節點
    else if(p.right!=null&&p.left!=null){

        //尋找替換結點
        p.data=findMin(p.right).data;

        //移除用於替換的結點
        p.right = remove( p.data, p.right );
    }
    else {
        //只有一個孩子結點或者只是葉子結點的情況
        p=(p.left!=null)? p.left:p.right;
    }

    //更新高度值
    if(p!=null)
        p.height = Math.max( height( p.left ), height( p.right ) ) + 1;
    return p;
}

平衡二叉樹的最少結點數和最多結點數問題

  關於最少結點數和最多結點數的問題，為了方便理解和簡單化問題，這裡我們假設AVL樹的高度是h，N(h)表示高度為h的AVL樹的結點數。對於求解高度為h的AVL樹的最少結點數，則應該儘可能用最少結點數來填充該樹，現在假設左子樹填充到的高度為h-1，根據AVL樹的特性，右子樹的高度只能填充到h-2，因此高度為h的AVL樹的最小結點數為：

N(h) = N(h-1) + N(h-2) + 1

其中：

• N(h-1) 代表高度為h-1的左子樹的最小結點數
• N(h-2) 代表高度為h-2的右子樹的最小結點數
• 1 代表當前結點(根)。

求解上述遞迴公式可得（計算過程涉及線性代數的知識點，這裡就不詳細分析求解過程，畢竟我們主要求時間複雜度相關問題）其中n是AVL樹的節點數：

N(h)=O(1.618h)=>h=1.44logn≈O(logn)

  通過上述的遞推公式，我們也可以發現最少結點數的求解公式恰好符合斐波那契數列的規律（F(n)=F(n-1)+F(n-2)），因此求解最少結點數也就變得容易多了。接著，我們採用同樣的方法計算最大結點數，為了得到最大結點數，則左右子樹的高必須相等，即都填充到h-1，由於結點都充滿了，那麼該樹不僅是AVL樹而且還是一個完全二叉樹了，則會有如下公式：

N(h) = N(h-1) + N(h-1) + 1 = 2N(h-1) + 1

最終求解該遞迴公式得：

N(h)=O(2h)=>h=logn≈O(logn)

  因此在兩種情況下，AVL樹的性質可以確保帶有n個結點的AVL樹的高度為O(logn)。這也意味著AVL樹的操作在時間複雜度上近乎於O(logn)，也就不可能出現BST(二叉查詢樹)的最糟糕情況O(n)。
  ok~，關於AVL樹就先聊到這，其他方法的實現跟上一篇的BST實現類似，大家直接看原始碼就行，本篇原始碼下載：github原始碼下載（含文章列表）