本文針對mnist手寫數字集，搭建了四層簡單的神經網路進行圖片的分類，詳細心得記錄下來分享
我是採用的TensorFlow框架進行的訓練

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

首先要載入資料集

#載入資料集
mnist = input_data.read_data_sets('MNIST_data',one_hot=True)
#設定批次大小
batch_size = 200
#計算批次數量
n_batch = mnist.train.num_examples // batch_size    
 

載入資料集可以直接呼叫input_data下的read_data_sets方法，括號裡的路徑我是放在了當前目錄下可以直接引用，當然也可以引用檔案的絕對路徑

x = tf.placeholder(tf.float32,[None,784])
y = tf.placeholder(tf.float32,[None,10])
keep_prob = tf.placeholder(tf.float32)

接著建立三個placeholder佔位符，None表示可以是任意維度的張量，784是由每一個手寫數字為28*28的畫素伸展成一維向量的原因，10表示待分為的0-910個類別，keep_prop表示神經網路訓練時設定神經元的存活率，如果為1，表示所有神經元參與工作，相當於不設定這個值，如果為0.6表示有60%的神經元參與工作。
然後搭建四層神經網路

#第一層隱藏層，2000個神經元
W1 = tf.Variable(tf.truncated_normal([784,2000],stddev=0.1))   
b1 = tf.Variable(tf.zeros([2000])+0.1)
L1 = tf.nn.tanh(tf.matmul(x,W1)+b1)
L1_drop = tf.nn.dropout(L1,keep_prob)

#第二層隱藏層
W2 = tf.Variable(tf.truncated_normal([2000,2000],stddev=0.1))
b2 = tf.Variable(tf.zeros([2000])+0.1)
L2 = tf.nn.tanh
 
(tf.matmul(L1,W2)+b2)
L2_drop = tf.nn.dropout(L2,keep_prob)

#第三層神經網路
W3 = tf.Variable(tf.truncated_normal([2000,1000],stddev=0.1))
b3 = tf.Variable(tf.zeros([1000])+0.1)
L3 = tf.nn.tanh(tf.matmul(L2,W3)+b3)
L3_drop = tf.nn.dropout(L3,keep_prob)

#第四層神經網路
W4 = tf.Variable(tf.truncated_normal([1000,10],stddev=0.1))
b4 = tf.Variable(tf.zeros([10])+0.1)
prediction = tf.nn.tanh(tf.matmul(L3,W4)+b4)

tf.truncated.normal為正態分佈函式，stddev表示標準差為0.1

W為權值矩陣，b為偏置值，在第一層中有784個輸入節點，2000個隱藏神經元。啟用函式使用的是雙曲正切函式tanh。值得注意的一點是，在每次計算Li的值時，需要使用Li-1的值和當前層數的權值矩陣加上當前層數的偏置值，在神經網路中表示由上一層的結果作用於本層神經網路，然後本層神經網路訓練的值接著作用於下一層，依次迴圈。

#loss = tf.reduce_mean(tf.square(y-prediction))
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y,logits=prediction))
optimizer = tf.train.GradientDescentOptimizer(0.4)
train = optimizer.minimize(loss)

註釋掉的loss是用的二次代價損失函式，第二行loss是用的交叉熵損失函式然後求平均值，如果不求平均值的話效果會比使用二次代價損失函式查，還不清楚原因（歡迎留言討論）。採用的梯度下降法來優化的，當然也可以採用其他的優化器，效果可以自己對比一下。

#初始化變數
init = tf.global_variables_initializer()

accuracy_prediction = tf.equal(tf.argmax(y,1),tf.argmax(prediction,1)) 
#計算準確率
accuracy = tf.reduce_mean(tf.cast(accuracy_prediction,tf.float32)) 

argmax表示返回一維張量最大值的位置，tf.equal(tf.argmax(y,1),tf.argmax(prediction,1)) 如果前面的位置和後面返回的位置一致，則輸出1，否則為0。比如tf.argmax(y,1)實際最大值位置為4，tf.argmax(prediction,1)預測最大值位置為4，則返回1。所以accuracy_prediction裡面存的全是布林型值。tf.cast(accuracy_prediction,tf.float32)是將前者變數轉換為後者資料型別

with tf.Session() as sess:
    sess.run(init)
    for epoch in range(20):
        for batch in range(n_batch):
            batch_xs,batch_ys = mnist.train.next_batch(batch_size)      #batch_xs每次獲得batch_size大小圖片，batch_ys獲得標籤
            sess.run(train,feed_dict={x:batch_xs,y:batch_ys,keep_prob:1.0}) #keep_prob值0.6表示6成神經元參與工作

        #每一輪輸出準確率
        test_acc = sess.run(accuracy,feed_dict={x:mnist.test.images,y:mnist.test.labels,keep_prob:0.6})
        train_acc = sess.run(accuracy, feed_dict={x: mnist.train.images, y: mnist.train.labels, keep_prob: 0.6})
        print('Iter:'+str(epoch)+' test_accuracy:'+str(test_acc)+' train_acc:'+str(train_acc))

根據keep_prob的值不同做了一個特意的對比實驗，當keep_prob的值設定為1時，訓練結果部分如下：

從結果可以看出，訓練的準確率比測試的準確率要高大約0.2個百分點，這樣看起來可能比較小，但是一旦當資料集擴大，這種差距會非常大，造成過擬合的現象。
再把keep_prob的值設定為0.6時，得到實驗結果如下

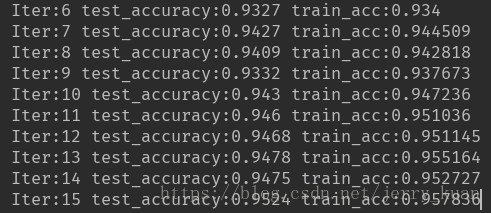
這樣兩者的差距在0.005左右，很大程度上緩解了過擬合現象。
原因因為當keep_prob的值設為1時所有的神經元全部參與，其實是相當於暴力的記憶住了當前的訓練集，因此在訓練集上有很好的效果，但是一旦離開這個訓練集，就會沒辦法擬合新的資料點而導致準確率下降。而當值適當減小時，其實就是模擬了人腦的記憶曲線，總會有些東西是會遺忘的，因而在訓練時雖然收斂的比較慢，但是泛化能力確增強了。