前言：這個程式碼是自己閒暇無事時候寫的。

因為CNN卷積神經網路用MNIST資料集、sklearn資料集程式碼很多部分都很相似，這一篇就不附詳細說明，原始碼最下。CNN卷積神經網路的工作原理，請詳情參考——【深度學習】5：CNN卷積神經網路原理、MNIST資料集識別
–—-—-—-—-—-—-—-—-—-—-—-—–—-—-—-—-—-—-—-——-—-—-—-—-—-—-—-—-—-—-—-—-—-——-
–—-—-—-—-—-—-—-—-—-—-—-—–—-—-—-—-—-—-—-——-—-—-—-—-—-—-—-—-—-—-—-—-—-——-

一、卷積神經網路原理介紹

用CNN卷積神經網路識別圖片，一般需要的步驟有：

1. 卷積層初步提取特徵
2. 池化層提取主要特徵
3. 全連線層將各部分特徵彙總
4. 產生分類器，進行預測識別

1.1、卷積層工作原理

卷積層的作用：就是提取圖片每個小部分裡具有的特徵

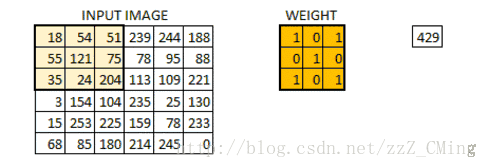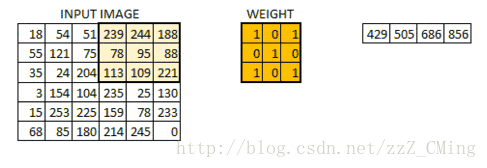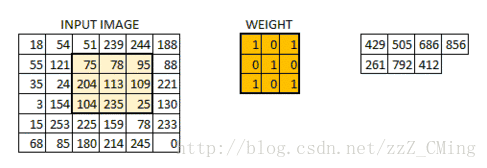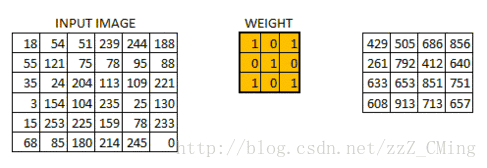
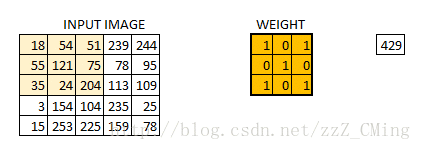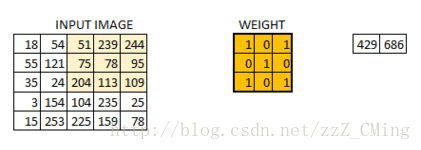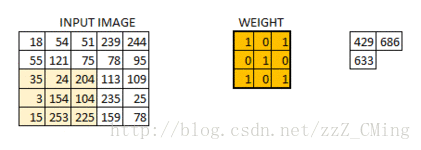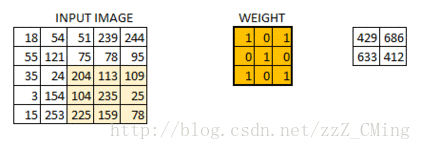
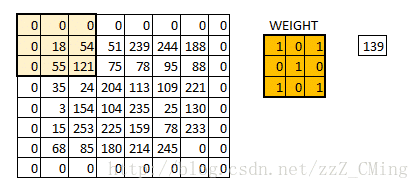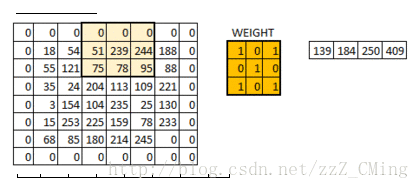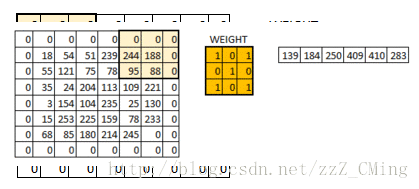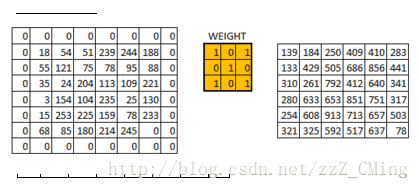
假定我們有一個尺寸為6*6 的影象，每一個畫素點裡都儲存著影象的資訊。我們再定義一個卷積核（相當於權重），用來從影象中提取一定的特徵。卷積核與數字矩陣對應位相乘再相加，得到卷積層輸出結果。

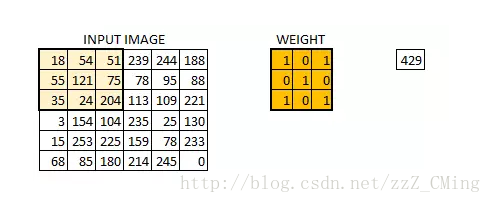
（429 = 18*1+54*0+51*1+55*0+121*1+75*0+35*1+24*0+204*1）
卷積核的取值在沒有以往學習的經驗下，可由函式隨機生成，再逐步訓練調整

當所有的畫素點都至少被覆蓋一次後，就可以產生一個卷積層的輸出（下圖的步長為1）

機器一開始並不知道要識別的部分具有哪些特徵，是通過與不同的卷積核相作用得到的輸出值，相互比較來判斷哪一個卷積核最能表現該圖片的特徵——比如我們要識別影象中的某種特徵（比如曲線），也就是說，這個卷積核要對這種曲線有很高的輸出值，對其他形狀（比如三角形）則輸出較低。卷積層輸出值越高，就說明匹配程度越高，越能表現該圖片的特徵。

卷積層具體工作過程：
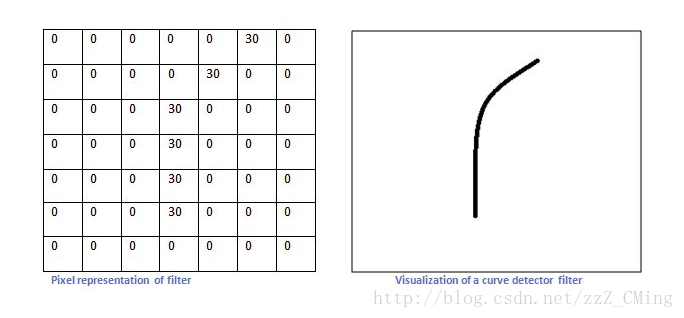
比如我們設計的一個卷積核如下左，想要識別出來的曲線如下右：

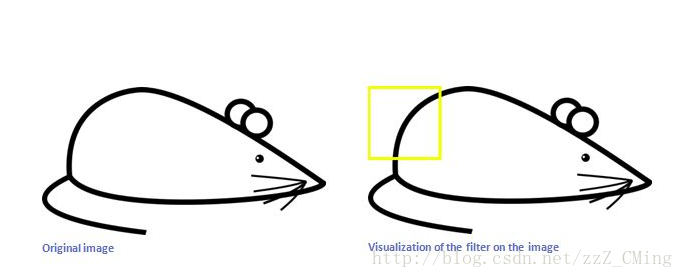
現在我們用上面的卷積核，來識別這個簡化版的圖片——一隻漫畫老鼠

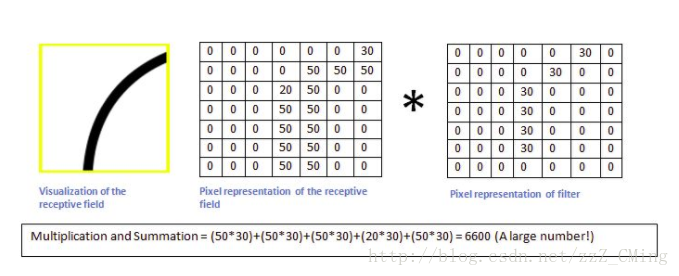
當機器識別到老鼠的屁股的時候，卷積核與真實區域數字矩陣作用後，輸出較大：6600

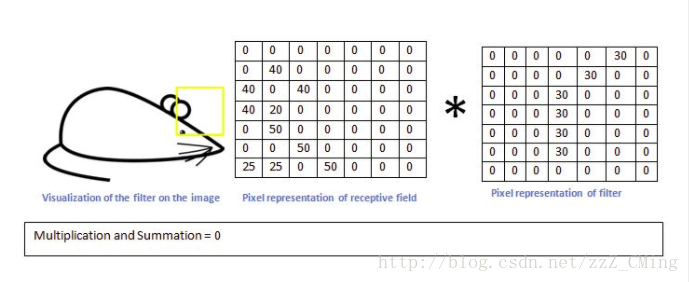
而用同一個卷積核，來識別老鼠的耳朵的時候，輸出則很小：0

我們就可以認為：現有的這個卷積核保存著曲線的特徵，匹配識別出來了老鼠的屁股是曲線的。我們則還需要其他特徵的卷積核，來匹配識別出來老鼠的其他部分。卷積層的作用其實就是通過不斷的改變卷積核，來確定能初步表徵圖片特徵的有用的卷積核是哪些，再得到與相應的卷積核相乘後的輸出矩陣

1.2、池化層工作原理

池化層的輸入就是卷積層輸出的原資料與相應的卷積核相乘後的輸出矩陣
池化層的目的：

• 為了減少訓練引數的數量，降低卷積層輸出的特徵向量的維度
• 減小過擬合現象，只保留最有用的圖片資訊，減少噪聲的傳遞

最常見的兩種池化層的形式：

• 最大池化：max-pooling——選取指定區域內最大的一個數來代表整片區域
• 均值池化：mean-pooling——選取指定區域內數值的平均值來代表整片區域

舉例說明兩種池化方式:（池化步長為2，選取過的區域，下一次就不再選取）

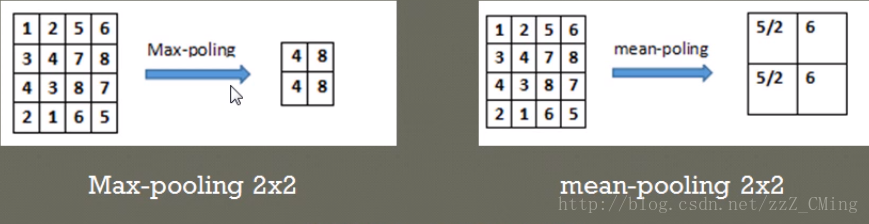
在4*4的數字矩陣裡，以步長2*2選取區域，比如上左將區域[1,2,3,4]中最大的值4池化輸出；上右將區域[1,2,3,4]中平均值5/2池化輸出

1.3、全連線層工作原理

卷積層和池化層的工作就是提取特徵，並減少原始影象帶來的引數。然而，為了生成最終的輸出，我們需要應用全連線層來生成一個等於我們需要的類的數量的分類器。

全連線層的工作原理和之前的神經網路學習很類似，我們需要把池化層輸出的張量重新切割成一些向量，乘上權重矩陣，加上偏置值，然後對其使用ReLU啟用函式，用梯度下降法優化引數既可。

二、卷積神經網路程式碼解析

2.1、資料集的讀取，以及資料預定義

# 讀取資料
digits = load_digits()
X_data = digits.data.astype(np.float32)
Y_data = digits.target.astype(np.float32).reshape(-1,1)

# 歸一化處理：最小最大值標準化
X_data = MinMaxScaler().fit_transform(X_data)
# 轉換為圖片的格式 （batch，height，width，channels）
X = X_data.reshape(-1,8,8,1)

# 標籤二值化：one-hot編碼
Y = OneHotEncoder().fit_transform(Y_data).todense()

'''
#歸一化的另一種方法
X_data -= X_data.min()
X_data /= X_data.max()
'''

• 資料為什麼要歸一化處理？當資料集的數值過大，即便乘以較小的權重後仍然還是一個很大的數時，當代入sigmoid啟用函式中，啟用函式的輸出就趨近於1，不利於學習
• 怎麼操作使資料歸一化？原始資料集中每一個數據先減去最小的那個數，將得到的新資料集再除以最大的那個數既可（大家可以舉個例子：2，7，5，9。試一試就知道）
• sklearn中直接一條語句就可以切分資料了：將資料項、標籤項切分出來，3/4做訓練集，剩下的1/4做測試集。
• 為什麼要標籤二值化？因為我們存入的標籤是0，1，2，，，9這十個數，而計算機的識別都是0-1字串，所以滿足計算機識別分類，就需要進行標籤二值化。
• 怎麼標籤二值化？舉例最好說明：用長度為10的字串表示如下：
  0 –>1000000000；3 –>0001000000；8 –>0000000010

2.2、權重、偏置值函式

def get_weight(shape):
    initial = tf.random_normal(shape)
    return tf.Variable(initial)

def get_baise(shape):
    initial = tf.random_normal(shape)
    return tf.Variable(initial)

truncated_normal()函式：選取位於正態分佈均值=0.1附近的隨機值

2.3、卷積函式、池化函式定義

#stride = [1,水平移動步長,豎直移動步長,1]
def conv2d(x,W,strides=[1, 1, 1, 1]):
    initial = tf.nn.conv2d(x,W,strides, padding='SAME')
    return initial

# stride = [1,水平移動步長,豎直移動步長,1]   
def max_pool_2x2(x):
    initial = tf.nn.max_pool(x,ksize=[1,3,3,1],strides=[1,2,2,1],padding='SAME')
    return initial

• 輸入x是圖片資訊矩陣，W是卷積核的值
• 卷積層conv2d()函式裡strides引數要求第一個、最後一個引數必須是1；
• 第二個引數表示：卷積核每次向右移動的步長
• 第三個引數表示：卷積核每次向下移動的步長

在上面卷積層的工作原理中，有展示strides=[1, 1, 1, 1]的動態圖，
下面展示strides=[1, 2, 2, 1]時的情況：可以看到高亮的區域每次向右移動兩格，向下移動兩格

可以得到：當我們的卷積層步長值越大，得到的輸出影象的規格就會越小。為了使得到的影象的規格和原影象保持一樣的大，在輸入影象四周填充足夠多的 0 邊界就可以解決這個問題，這時padding的引數就為“SAME”（利用邊界保留了更多資訊，並且也保留了影象的原大小）下圖：

padding的另一個可選引數為“VALID”，和“SAME”不同的是：不用0來填充邊界，這時得到的影象的規格就會小於原影象。新影象尺寸大小 = 原資料尺寸大小-卷積核尺寸大小+1（一般我們選用的padding都為“SAME”）

池化函式用簡單傳統的2x2大小的模板做max pooling，池化步長為2，選過的區域下次不再選取

2.4、第一次卷積+池化

# 卷積層1 + 池化層1
W_conv1 = get_weight([3, 3, 1, 10])
b_conv1 = get_baise([10])
h_conv1 = tf.nn.relu(conv2d(x, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1) 

• 這裡的卷積核大小是3*3的，輸入的通道數是1，輸出的通道數是10
• 卷積核的值這裡就相當於權重值，用隨機數列生成的方式得到

2.5、第二次卷積+池化

# 卷積層2
W_conv2 = get_weight([3, 3, 10, 5])
b_conv2 = get_baise([5])
h_conv2 = conv2d(h_conv1, W_conv2,strides=[1, 2, 2, 1]) + b_conv2

# BN歸一化層 + 啟用層
batch_mean, batch_var = tf.nn.moments(h_conv2, [0, 1, 2], keep_dims=True)
shift = tf.Variable(tf.zeros([5]))
scale = tf.Variable(tf.ones([5]))
BN_out = tf.nn.batch_normalization(h_conv2, batch_mean, batch_var, shift, scale,lr)
relu_BN_maps2 = tf.nn.relu(BN_out)

# 池化層2 + 全連線層1
h_pool2 = max_pool_2x2(relu_BN_maps2)                        

• 這裡的卷積核大小也是3*3的，第二次輸入的通道數是10，輸出的通道數是5

2.6、全連線層1、全連線層2

# 全連線層1
h_pool2_flat = tf.reshape(h_pool2, [-1, 2*2*5])
W_fc = get_weight([2*2*5,50])
b_fc = get_baise([50])
fc_out = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc) + b_fc)

# 輸出層
W_out = get_weight([50,10])
b_out = get_baise([10])
pred = tf.nn.softmax(tf.matmul(fc_out,W_out)+b_out)

• 全連線層的輸入就是第二次池化後的輸出，全連線層1有50個神經元
• 全連線層2有10個神經元，相當於生成的分類器
• 經過全連線層1、2，得到的預測值存入pred 中

2.7、梯度下降法優化、求準確率

# 計算誤差、梯度下降法減小誤差、求準確率
#loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=pred))
loss = -tf.reduce_mean(y_*tf.log(tf.clip_by_value(pred,1e-11,1.0)))
train_step = tf.train.AdamOptimizer(1e-2).minimize(loss)
y_pred = tf.arg_max(pred,1)
bool_pred = tf.equal(tf.arg_max(y_,1),y_pred)
accuracy = tf.reduce_mean(tf.cast(bool_pred,tf.float32)) # 準確率

• 由於資料集太龐大，這裡採用的優化器是AdamOptimizer，學習率是1e-4
• bool_pred 這裡是返回一個布林陣列。為了計算我們分類的準確率，我們將布林值轉換為浮點數來代表對與錯，然後取平均值。例如：[True, False, True, True]變為[1,0,1,1]，計算出準確率就為0.75

三、原始碼以及準確率展示

# -*- coding:utf-8 -*-
# -*- author：zzZ_CMing
# -*- 2018/03/25 18:40
# -*- python3.5

"""
程式有時會陷入區域性最小值，導致準確率在一定數值浮動，可以重新執行程式
"""

import pylab as pl
import numpy as np
import tensorflow as tf
from sklearn.datasets import load_digits
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import OneHotEncoder
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

def get_batch(X,Y,n_examples, batch_size):
    for batch_i in range(n_examples // batch_size):
        start = batch_i*batch_size
        end = start + batch_size
        batch_xs = X[start:end]
        batch_ys = Y[start:end]
        yield batch_xs, batch_ys # 生成每一個batch

def get_weight(shape):
    initial = tf.random_normal(shape)
    return tf.Variable(initial)

def get_baise(shape):
    initial = tf.random_normal(shape)
    return tf.Variable(initial)

def conv2d(x,W,strides=[1, 1, 1, 1]):
    initial = tf.nn.conv2d(x,W,strides, padding='SAME')
    return initial

def max_pool_2x2(x):
    initial = tf.nn.max_pool(x,ksize=[1,3,3,1],strides=[1,2,2,1],padding='SAME')
    return initial

lr = 1e-3

# 讀取資料
digits = load_digits()
X_data = digits.data.astype(np.float32)
Y_data = digits.target.astype(np.float32).reshape(-1,1)
# 歸一化處理：最小最大值標準化
X_data = MinMaxScaler().fit_transform(X_data)
# 轉換為圖片的格式 （batch，height，width，channels）
X = X_data.reshape(-1,8,8,1)
# 標籤二值化：one-hot編碼
Y = OneHotEncoder().fit_transform(Y_data).todense()
'''
#歸一化的另一種方法
X_data -= X_data.min()
X_data /= X_data.max()
'''

# 預定義x，y_
x = tf.placeholder(tf.float32,[None,8,8,1])
y_ = tf.placeholder(tf.float32,[None,10])

# 卷積層1 + 池化層1
W_conv1 = get_weight([3, 3, 1, 10])
b_conv1 = get_baise([10])
h_conv1 = tf.nn.relu(conv2d(x, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)

# 卷積層2
W_conv2 = get_weight([3, 3, 10, 5])
b_conv2 = get_baise([5])
h_conv2 = conv2d(h_conv1, W_conv2,strides=[1, 2, 2, 1]) + b_conv2

# BN歸一化層 + 啟用層
batch_mean, batch_var = tf.nn.moments(h_conv2, [0, 1, 2], keep_dims=True)
shift = tf.Variable(tf.zeros([5]))
scale = tf.Variable(tf.ones([5]))
BN_out = tf.nn.batch_normalization(h_conv2, batch_mean, batch_var, shift, scale,lr)
relu_BN_maps2 = tf.nn.relu(BN_out)

# 池化層2 + 全連線層1
h_pool2 = max_pool_2x2(relu_BN_maps2)
h_pool2_flat = tf.reshape(h_pool2, [-1, 2*2*5])
W_fc = get_weight([2*2*5,50])
b_fc = get_baise([50])
fc_out = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc) + b_fc)

# 輸出層
W_out = get_weight([50,10])
b_out = get_baise([10])
pred = tf.nn.softmax(tf.matmul(fc_out,W_out)+b_out)

# 計算誤差、梯度下降法減小誤差、求準確率
#loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=pred))
loss = -tf.reduce_mean(y_*tf.log(tf.clip_by_value(pred,1e-11,1.0)))
train_step = tf.train.AdamOptimizer(1e-2).minimize(loss)
y_pred = tf.arg_max(pred,1)
bool_pred = tf.equal(tf.arg_max(y_,1),y_pred)
accuracy = tf.reduce_mean(tf.cast(bool_pred,tf.float32)) # 準確率
'''
# 用下面的，準確率只在90%左右
correct_prediction = tf.equal(tf.argmax(pred,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
'''

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    # 迭代1000個週期，每個週期進行MBGD演算法
    for i in range(101):
        for batch_xs,batch_ys in get_batch(X,Y,Y.shape[0],batch_size=8):
            sess.run(train_step,feed_dict={x:batch_xs,y_:batch_ys})
        if(i%10==0):
            res = sess.run(accuracy,feed_dict={x:X,y_:Y})
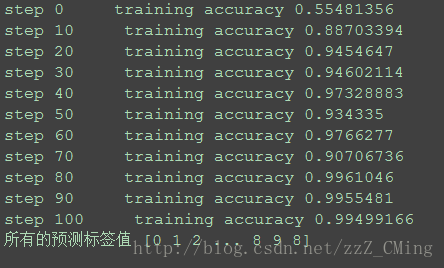
            print ("step",i, "    training accuracy",res)

        # 只能預測一批樣本，不能預測一個樣本
    res_ypred = y_pred.eval(feed_dict={x: X, y_: Y}).flatten()
    print('所有的預測標籤值', res_ypred)

    """
    # 下面是打印出前15張圖片的預測標籤值、以及第5張圖片
    print('預測標籤', res_ypred[0:15])
    pl.gray()
    pl.matshow(digits.images[4])
    pl.show()
    """

結果展示：

sklearn資料集中的圖片大小都是8*8的，所以識別的速度、準確率都是比較高的
–—-—-—-—-—-—-—-—-—-—-—-—–—-—-—-—-—-—-—-——-—-—-—-—-—-—-—-—-—-—-—-—-—-——-
–—-—-—-—-—-—-—-—-—-—-—-—–—-—-—-—-—-—-—-——-—-—-—-—-—-—-—-—-—-—-—-—-—-——-

系列推薦：