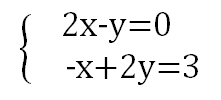麻省理工公開課:線性代數_學習筆記01
阿新 • • 發佈:2018-11-09
方程組的幾何解釋
最近愈發覺得3D數學基礎這本書裡的數學看不太懂,就決定放下這本書,先系統學習一遍線性代數。
之後找到了一套線性代數很棒的視訊,麻省理工大學教授講的。下面會依次來做筆記
二元一次方程組中的幾何解釋
e.g.
可以得出係數矩陣

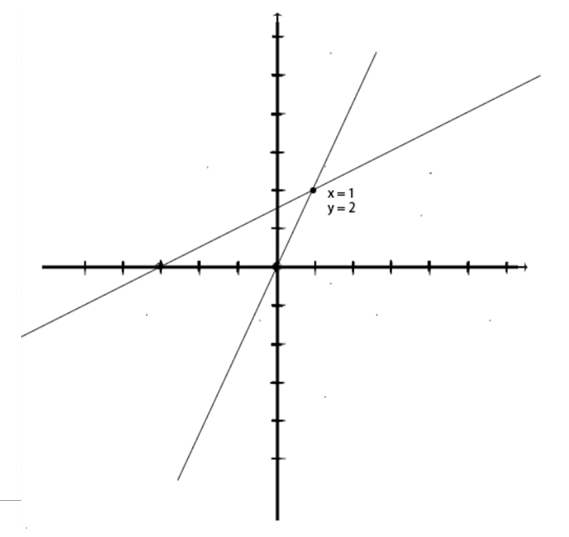
行影象Row Picture
其實也就是之前一直學習的普通座標系的方法
令x為-1 和 y為0就能迅速得出以下座標系和交點(1,2)
列影象 column picture

簡要來說就是把方程組內的係數從列看,看成向量,然後在座標系上就顯示為直觀的向量加減法。這樣向量先乘以一個標量(這裡指x或y)再進行加減的方法被稱為線性組合
(linear combination)。

三元一次方程組中的幾何解釋
e.g.
同樣先畫出他的
Row picture
由於三維向量太難用PS畫,我選擇用紙畫
不難想象最後會發現表現單個方程所有解的影象形成一個平面,最後方程組的解結果為三個平面相交。(這裡就應付著隨便畫畫我寫這玩意已經花了1
Column picture
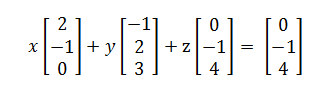
按得出來的列的係數矩陣,可以馬上得到一個解(0、0、1)。
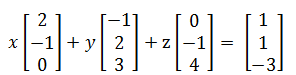
現在可以改變右測向量,因為只是簡單的加減前兩個矩陣,答案是(1,1,0)
最後有一個定義需要記憶,類的線性組合只有在三個列向量為不同平面時才能覆蓋整個三維空間,當有列向量同一平面時,被稱作奇藝矩陣,該矩陣不可逆。