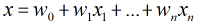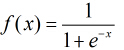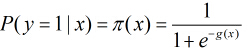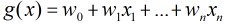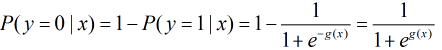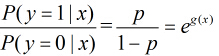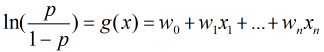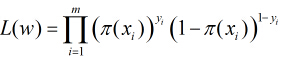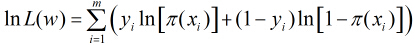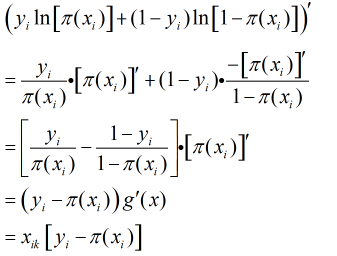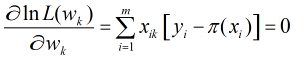Logistic迴歸原理及公式推導
Logistic迴歸為概率型非線性迴歸模型,是研究二分類觀察結果
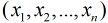
在講解Logistic迴歸理論之前,我們先從LR分類器說起。LR分類器,即Logistic Regression Classifier。
在分類情形下,經過學習後的LR分類器是一組權值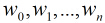
這裡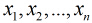
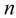
之後按照sigmoid函式的形式求出
由於sigmoid函式的定義域為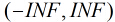
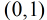
所以Logistic迴歸最關鍵的問題就是研究如何求得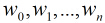
下面正式地來講Logistic迴歸模型。
考慮具有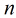
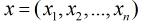
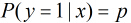
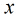

這裡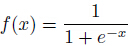
那麼在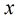

所以事件發生與不發生的概率之比為
這個比值稱為事件的發生比(the odds of experiencing an event),簡記為odds。
對odds取對數得到
可以看出Logistic迴歸都是圍繞一個Logistic函式來展開的。接下來就講如何用極大似然估計求分類器的引數。
假設有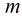
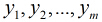
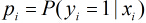
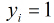
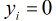
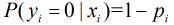
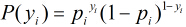
因為各個觀測樣本之間相互獨立,那麼它們的聯合分佈為各邊緣分佈的乘積。得到似然函式為
然後我們的目標是求出使這一似然函式的值最大的引數估計,最大似然估計就是求出引數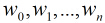
取得最大值,對函式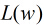
繼續對這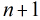
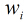
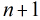
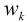
所以得到
這樣的方程一共有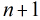
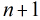
上述方程比較複雜,一般方法似乎不能解之,所以我們引用了牛頓-拉菲森迭代方法求解。
利用牛頓迭代求多元函式的最值問題以後再講。。。
簡單牛頓迭代法:http://zh.m.wikipedia.org/wiki/%E7%89%9B%E9%A1%BF%E6%B3%95
實際上在上述似然函式求最大值時,可以用梯度上升演算法,一直迭代下去。梯度上升演算法和牛頓迭代相比,收斂速度
慢,因為梯度上升演算法是一階收斂,而牛頓迭代屬於二階收斂。
以上內容來自使用者【演算法學習者】部落格,僅作部分格式和詞語修改。原文地址:http://blog.csdn.net/amds123/article/details/70243497