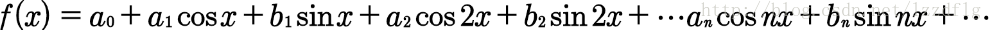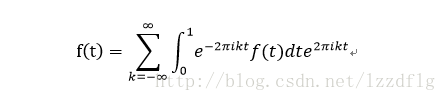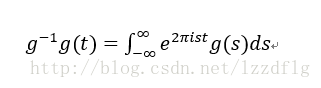傅立葉變換概念及公式推導
傅立葉變換(FT)
傅立葉變換的目的是可將時域(即時間域)上的訊號轉變為頻域(即頻率域)上的訊號,隨著域的不同,對同一個事物的瞭解角度也就隨之改變,因此在時域中某些不好處理的地方,在頻域就可以較為簡單的處理。
傅立葉變換公式:
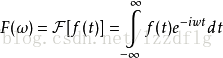
(w代表頻率,t代表時間,e^-iwt為複變函式)
傅立葉變換認為一個周期函式(訊號)包含多個頻率分量,任意函式(訊號)f(t)可通過多個周期函式(基函式)相加而合成。
從物理角度理解傅立葉變換是以一組特殊的函式(三角函式)為正交基,對原函式進行線性變換,物理意義便是原函式在各組基函式的投影
傅立葉公式推導:
我們先從函式f(t)為週期性函式推導,之後推導非週期性函式的傅立葉變換,傅立葉公式一般就是指非週期行函式的傅立葉變換(FT)。
(1)對於週期為1的函式f(t):
(這裡的x我接下來用t來表示)
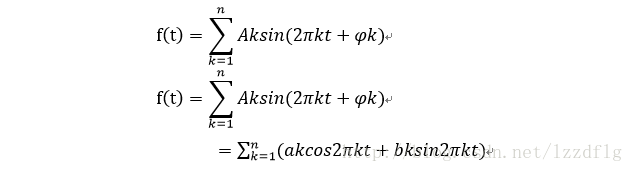
根據尤拉公式
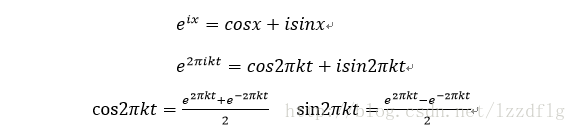

這裡的Ck是一個複數,Ck一般稱為傅立葉係數,平時對頻域的變換,一般改變的就是Ck。
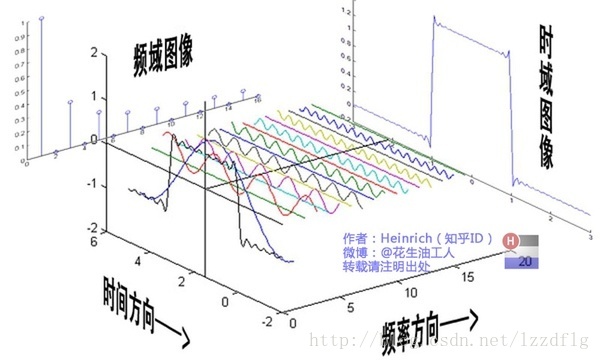
例如這個圖中頻域方向上的圖每個頻域值為Ck的值
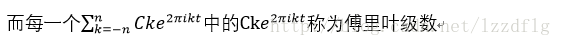
接下來求Ck的值
由
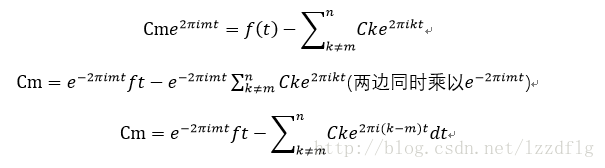
對函式兩邊積分
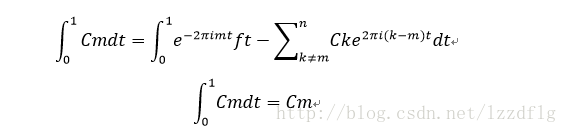
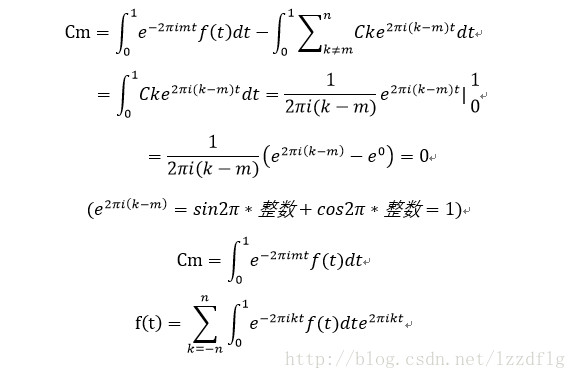
(上述的k指頻域上的x座標,每個k值為一種赫茲,t表示時域上的時間)
因為要模擬一個訊號,訊號是不能通過有限個周期函式相加而確定這樣會有很大的誤差,無法得到完整的近似值,於是我們便用無限的周期函式來對其近似
由此就可以看出傅立葉變換是一種時域與頻域的轉換關係。
(2)對於非周期函式f(t)
對於一個訊號的處理,訊號一般都不是週期的,因此這裡就產生了對非周期函式(訊號)的處理。
對於非周期函式我們可以假設為非周期函式是一個周期函式的某個部分,但這個非周期函式的t範圍可以非常的大。
傅立葉變換當週期趨近於無窮,是傅立葉係數的一般化
傅立葉逆變換是對傅立葉級數的一般化
設f(t)是週期為T的函式,T趨近於無窮的周期函式
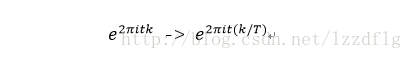
傅立葉級數[f(t)]轉變為
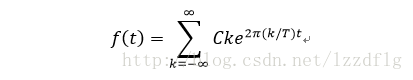
傅立葉係數為(注:因在無限大的週期T下所以從0->T與(-T/2)->(T/2)是相同的)

在頻譜圖中你看到的每一條豎線就是|CK|的值
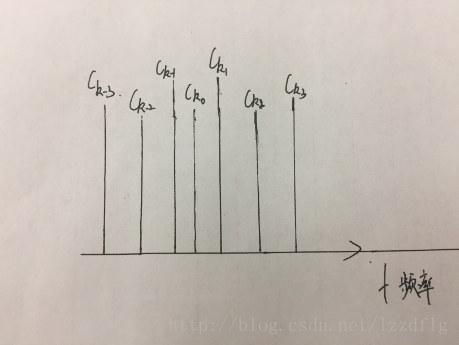
這就是一個在時域上的函式影象經過傅立葉變換轉換的頻譜圖。
很重要的一點是 :
對於週期為1的函式頻域上每條線的間隔為1
而對於週期為T的函式,頻域上的間隔為1/T
時域週期與頻域有反比的關係。
即 T<1 ->1/T>1 頻譜會被擴充套件
當 T>1 ->1/T<1 頻譜會被壓縮
特別的當T趨近於無窮,頻譜間隔越來越近,最終頻譜變為連續的。
由此可以得到一句經常看到的話,當時域從週期轉化為非週期時,頻域從離散的轉化為連續的。
看來把一個非周期函式看作是一個周期函式的一部分這樣就能的出傅立葉變換的結果了莫?
其實是這樣是不完全正確的。因為當T趨近於無窮時Ck會趨向於零使得整個傅立葉係數的公式沒有意義:
設f(t)在區間a,b之間其他為0,取一個大的週期T使a>-T/2&&b>T/2,然後以T為函式擴充套件(|Ck|因為是複函式所以關於x軸對稱)
如下圖:

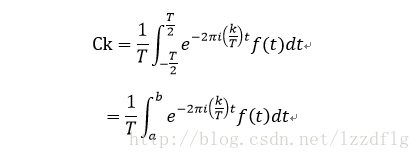
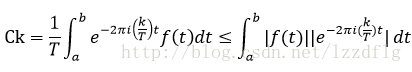
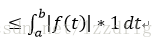
即
即 Ck=0。
連每個頻率的係數都是0,那這f(t)還有什麼用。
為此我們從另一個角度看
設gf這個公式為關於k/T的函式: gf(k/T)
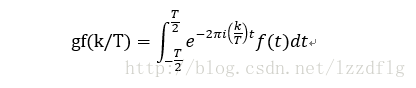
(即Ck不要1/T的部分)

(這裡和上面推導f(t)的結果是一樣的)
因T->∞,gf(k/T)中k/T這個離散變數之間越來越趨近,1/T,2/T,3/T……這樣函式就從離散的變為連續,我們將這個k/T連續變數設為s
這樣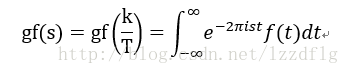
關於f(t),f(t)可以看作無數個連續的gf(s)e^2πist,乘以1/T來組成將其看作累加和變換為積分。即
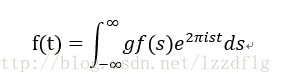
這樣我們就最終得到了傅立葉變換公式(FT)(傅立葉變換也可以稱為一種運算元):
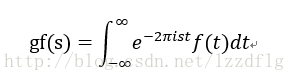
順便給出傅立葉反變換公式:
文章參考:https://www.zhihu.com/question/19714540
https://www.zhihu.com/question/38841975
斯坦福大學課程:傅立葉變換及其應用