反向傳播演算法(過程及公式推導)
阿新 • • 發佈:2019-01-08
反向傳播演算法(Backpropagation)是目前用來訓練人工神經網路(Artificial Neural Network,ANN)的最常用且最有效的演算法。其主要思想是:
(1)將訓練集資料輸入到ANN的輸入層,經過隱藏層,最後達到輸出層並輸出結果,這是ANN的前向傳播過程; (2)由於ANN的輸出結果與實際結果有誤差,則計算估計值與實際值之間的誤差,並將該誤差從輸出層向隱藏層反向傳播,直至傳播到輸入層; (3)在反向傳播的過程中,根據誤差調整各種引數的值;不斷迭代上述過程,直至收斂。 反向傳播演算法的思想比較容易理解,但具體的公式則要一步步推導,因此本文著重介紹公式的推導過程。1. 變數定義
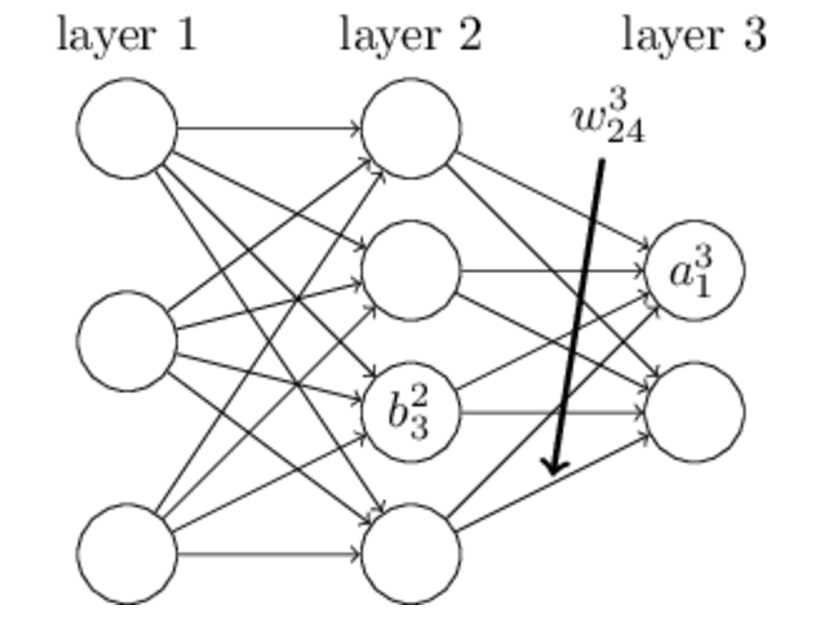
上圖是一個三層人工神經網路,layer1至layer3分別是輸入層、隱藏層和輸出層。如圖,先定義一些變數:
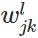 表示第
表示第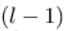 層的第
層的第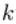 個神經元連線到第
個神經元連線到第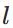 層的第
層的第 個神經元的權重;
個神經元的權重;
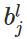 表示第
表示第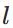 層的第
層的第 個神經元的偏置;
個神經元的偏置;
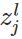 表示第
表示第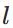 層的第
層的第 個神經元的輸入,即:
個神經元的輸入,即:
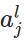 表示第
表示第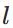 層的第
層的第 個神經元的輸出,即:
個神經元的輸出,即:
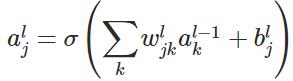 其中
其中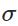 表示啟用函式。
表示啟用函式。
2. 代價函式
代價函式被用來計算ANN輸出值與實際值之間的誤差。常用的代價函式是二次代價函式(Quadratic cost function):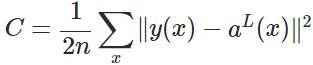
其中,
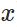 表示輸入的樣本,
表示輸入的樣本,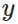 表示實際的分類,
表示實際的分類,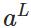 表示預測的輸出,
表示預測的輸出,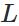 表示神經網路的最大層數。
表示神經網路的最大層數。
3. 公式及其推導
本節將介紹反向傳播演算法用到的4個公式,並進行推導。如果不想了解公式推導過程,請直接看第4節的演算法步驟。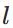 層第
層第 個神經元中產生的錯誤(即實際值與預測值之間的誤差)定義為:
個神經元中產生的錯誤(即實際值與預測值之間的誤差)定義為:
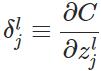 本文將以一個輸入樣本為例進行說明,此時代價函式表示為:
本文將以一個輸入樣本為例進行說明,此時代價函式表示為:
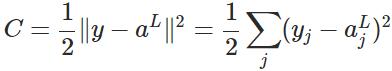
公式1(計算最後一層神經網路產生的錯誤):
其中,
 表示Hadamard乘積,用於矩陣或向量之間點對點的乘法運算。公式1的推導過程如下:
表示Hadamard乘積,用於矩陣或向量之間點對點的乘法運算。公式1的推導過程如下:
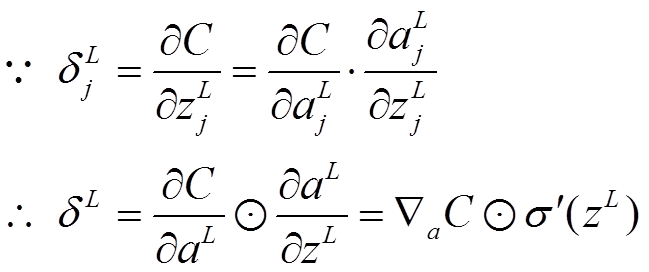
公式2(由後往前,計算每一層神經網路產生的錯誤):
推導過程:
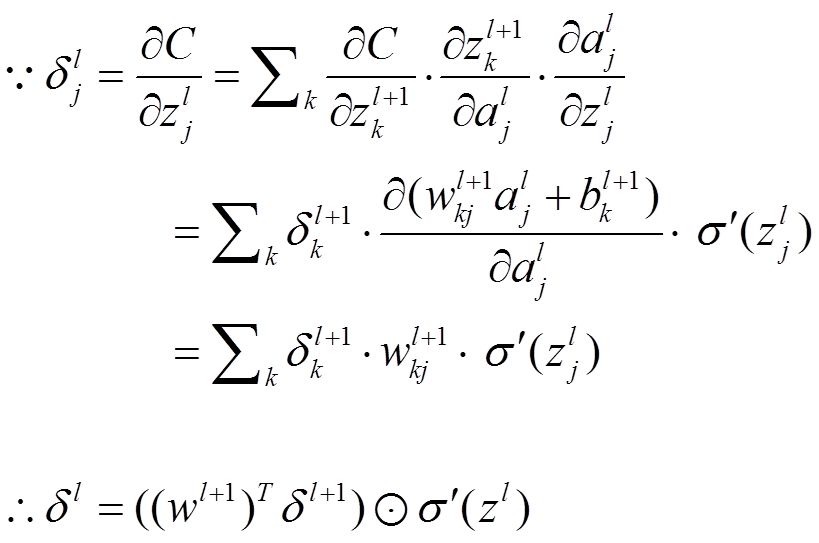 公式3(計算權重的梯度):
公式3(計算權重的梯度):
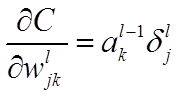
推導過程:
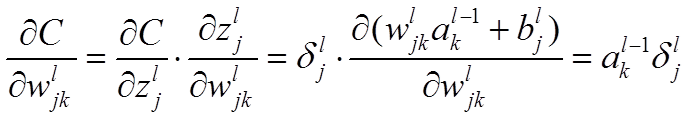
公式4(計算偏置的梯度):
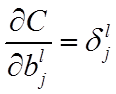
推導過程:
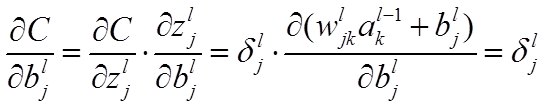
4. 反向傳播演算法虛擬碼
- 輸入訓練集
- 對於訓練集中的每個樣本x,設定輸入層(Input layer)對應的啟用值
:
- 前向傳播:
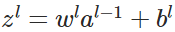 ,
, 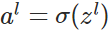
- 計算輸出層產生的錯誤:
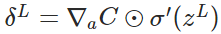
- 反向傳播錯誤:
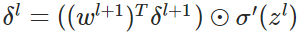
- 使用梯度下降(gradient descent),訓練引數:
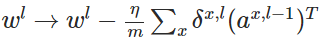
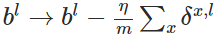
原文地址:http://m.blog.csdn.net/article/details?id=51039334
