（這裡是本章會用到的 GitHub 地址）

（感謝評論區

RNN 的“前向傳導演算法”

在說明如何進行訓練之前，我們先來回顧一下 RNN 的“前向傳導演算法。在上一章中曾經給過一個沒有啟用函式和變換函式的公式：

在實現層面來說，這就是一個迴圈的事兒，所以程式碼寫起來會比較簡單：

import numpy as np

class RNN1:
    def __init__(self, u, v, w):
        self._u, self._v, self._w = np.asarray
 
(u), np.asarray(v), np.asarray(w)
        self._states = None

    # 啟用函式
    def activate(self, x):
        return x

    # 變換函式
    def transform(self, x):
        return x

    def run(self, x):
        output = []
        x = np.atleast_2d(x)
        # 初始化 States 矩陣為零矩陣
        # 之所以把所有 States 記下來、是因為訓練時（BPTT 演算法）要用到
 

        self._states = np.zeros([len(x)+1, self._u.shape[0]])
        for t, xt in enumerate(x):
            # 對著公式敲程式碼即可 ( σ'ω')σ
            self._states[t] = self.activate(
                self._u.dot(xt) + self._w.dot(self._states[t-1])
            )
            output.append(self.transform(
                self
 
._v.dot(self._states[t]))
            )
        return np.array(output)

可以用上一章說過的那個小栗子來測試一下：

• 假設現在是單位陣，是單位陣的兩倍
  
• 假設輸入序列為：

對應的測試程式碼如下：

n_sample = 5
rnn = RNN1(np.eye(n_sample), np.eye(n_sample), np.eye(n_sample) * 2)
print(rnn.run(np.eye(n_sample)))

程式輸出為：

這和我們上一章推出的理論值是一致的（）

RNN 的“反向傳播演算法”

簡潔起見，我們採用上一章第一張圖所示的那個樸素網路結構：

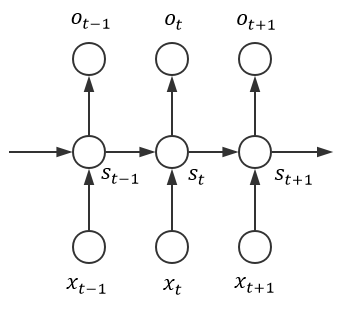
然後做出如下符號約定：

• 取作為隱藏層的啟用函式
• 取作為輸出層的變換函式
• 取作為模型的損失函式，其中標籤是一個 one-hot 向量；由於 RNN 處理的通常是序列資料、所以在接受完序列中所有樣本後再統一計算損失是合理的，此時模型的總損失可以表示為（假設輸入序列長度為）：

為了更清晰地表明各個配置，我們可以整理出如下圖所示的結構：

易知，其中。令：

則有：

從而（注：統一使用“”表示 element wise 乘法，使用“”表示矩陣乘法）：

可見對矩陣的分析過程即為普通的反向傳播演算法，相對而言比較平凡。由可知，它的總梯度可以表示為：

而事實上，RNN 的 BP 演算法的主要難點在於它 State 之間的通訊，亦即梯度除了按照空間結構傳播（）以外，還得沿著時間通道傳播（），這導致我們比較難將相應 RNN 的 BP 演算法寫成一個統一的形式（回想之前的“前向傳導演算法”）。為此，我們可以採用“迴圈”的方法來計算各個梯度

由於是反向傳播演算法，所以應從開始降序迴圈至 1，在此期間（若需要初始化、則初始化為 0 向量或 0 矩陣）：

• 計算時間通道上的“區域性梯度” ：
  
• 利用時間通道上的“區域性梯度”計算和的梯度：
  

以上即為 RNN 反向傳播演算法的所有推導，它比 NN 的 BP 演算法要繁複不少。事實上，像這種需要把梯度沿時間通道傳播的 BP 演算法是有一個專門的名詞來描述的——Back Propagation Through Time（常簡稱為 BPTT，可譯為“時序反向傳播演算法”）

不妨舉一個具體的栗子來加深理解，假設：

• 啟用函式為 Sigmoid 函式
• 變換函式為 Softmax 函式
• 損失函式為 Cross Entropy（感謝評論區 @格子非 指出這裡的錯誤）：

由 NN 處的討論可知這是一個非常經典、有效的配置，其中：

從而

且從開始降序迴圈至 1 的期間中，各個“區域性梯度”為：

由此可算出如下相應梯度：

可以看到形式相當簡潔，所以我們完全可以比較輕易地寫出相應實現：

class RNN2(RNN1):
    # 定義 Sigmoid 啟用函式
    def activate(self, x):
        return 1 / (1 + np.exp(-x))

    # 定義 Softmax 變換函式
    def transform(self, x):
        safe_exp = np.exp(x - np.max(x))
        return safe_exp / np.sum(safe_exp)

    def bptt(self, x, y):
        x, y, n = np.asarray(x), np.asarray(y), len(y)
        # 獲得各個輸出，同時計算好各個 State
        o = self.run(x)
        # 照著公式敲即可 ( σ'ω')σ
        dis = o - y
        dv = dis.T.dot(self._states[:-1])
        du = np.zeros_like(self._u)
        dw = np.zeros_like(self._w)
        for t in range(n-1, -1, -1):
            st = self._states[t]
            ds = self._v.T.dot(dis[t]) * st * (1 - st)
            # 這裡額外設定了最多往回看 10 步
            for bptt_step in range(t, max(-1, t-10), -1):
                du += np.outer(ds, x[bptt_step])
                dw += np.outer(ds, self._states[bptt_step-1])
                st = self._states[bptt_step-1]
                ds = self._w.T.dot(ds) * st * (1 - st)
        return du, dv, dw

    def loss(self, x, y):
        o = self.run(x)
        return np.sum(
            -y * np.log(np.maximum(o, 1e-12)) -
            (1 - y) * np.log(np.maximum(1 - o, 1e-12))
        )

注意我們設定了在每次沿時間通道反向傳播時、最多往回看 10 步，這是因為我們實現的這種樸素 RNN 的梯度存在著一些不良性質，我們在下一節中馬上就會進行相關的說明

指數級梯度所帶來的問題

注意到由於 RNN 需要沿時間通道進行反向傳播，其相應的“區域性梯度”為：

注意到式中的每個區域性梯度都會“攜帶”一個矩陣和一個的 Sigmoid 系啟用函式所對應的梯度，這意味著區域性梯度受和各個啟用函式的梯度的影響是指數級的。姑且不考慮而單看啟用函式的梯度，回憶我們之前在 NN 處講過的梯度問題，這裡的這種指數級梯度的表現和彼時深層網路梯度的表現是幾乎同理的（事實上 RNN 的時間通道長得確實很像一個深層網路）——當輸入趨近於兩端時，啟用函式的梯度會隨著傳播而迅速彌散，這就是 RNN 中所謂的“梯度消失（The Vanishing Gradient）”問題。是故我們在上一小節實現 RNN 時規定在沿時間通道反向傳播時最多隻往回看 10 步，這是因為再往下看也沒有太大意義了（可以大概地類比於多於 10 層的、以 Sigmoid 系函式作為啟用函式的神經網路）（以下純屬開腦洞：這麼說的話是不是能在時間通道里面傳遞殘差然後弄一個 Residual RNN 呢……）

這當然是非常令人沮喪的結果，要知道 RNN 的一大好處就在於它能利用上歷史的資訊，然而梯度消失卻告訴我們 RNN 能夠利用的歷史資訊十分有限。所以針對該問題作出優化是非常有必要的，解決方案大體上分兩種：

• 選用更好的啟用函式
• 改進 State 的傳遞方式

第二點是 LSTMs 等特殊 RNN 的做法，這裡就主要說說第一點——如何選用更好的啟用函式。由 NN、CNN 處的討論不難想到，用 ReLU 作為啟用函式很有可能是個不錯的選擇；不過由於梯度是指數級的這一點不會改變，此時我們可能就會面臨另一個問題：“梯度爆炸（The Exploding Gradient）”（注：不是說 Sigmoid 系函式就不會引發梯度爆炸、因為當矩陣的元素很大時同樣會爆炸，只是相對而言更容易引發梯度消失而已）。不過相比起梯度消失問題來講，梯度爆炸相對而言要顯得更“友好”一些，這是因為：

• 梯度爆炸一旦發生，是會迅速反映到結果上來的（比如一堆數變成了 NaN）
• 梯度爆炸可以通過簡單的設定閾值來得到改善

而梯度消失相比之下，既難以直接從結果看出、又沒有特別平凡的解決方案。現有的較常用的方法為調整引數的初值、進行適當的正則化、使用 ReLU（需要小心梯度爆炸）等等

關於為何 LSTMs 能夠解決梯度消失，直觀上來說就是上方時間通道是簡單的線性組合、從而使得梯度不再是指數級的。詳細的推導可以參見各種論文（比如說這篇），我就不在這裡獻醜了 ( σ'ω')σ

以上就大致地說了說 RNN 的 BPTT 演算法，主要要注意的其實就是時間通道上的 BP 演算法。如果把時間通道看成一個神經網路的話，運用區域性梯度來反向傳播其實相當自然