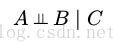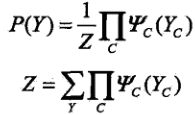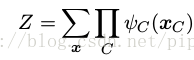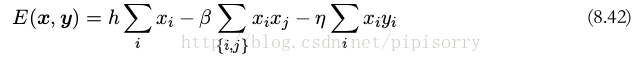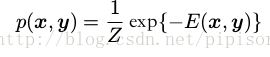http://blog.csdn.net/pipisorry/article/details/78396503

馬爾可夫網

馬爾科夫網是使用無向圖描述的圖模型，是刻畫X上聯合分佈的一種方法，表示一個分解方式,也表示一組條件獨立關係。馬爾科夫隨機場( Markov random field , MRF),也被稱為馬爾科夫網路( Markov network )或者無向圖模型( undirected graphical model )( Kindermann and Snell, 1980 ),包含一組結點,每個結點都對應著一個變數或一組變數。連結是無向的,即不含有箭頭。

與貝葉斯網一樣，馬爾可夫網可以視為定義了一系列由圖結構確定的獨立性假設。

條件獨立性質

定義一種概率分佈的圖語義表示,使得條件獨立性由單一的圖劃分確定。

假設在一個無向圖中,我們有三個結點集合,記作 A, B, C 。我們考慮條件獨立性質

為了判定由圖定義的概率分佈是否滿足這個性質,我們考慮連線集合 A 的結點和集合 B 的結點的所有可能路徑。如果所有這些路徑都通過了集合 C 中的一個或多個結點,那麼所有這樣的路徑都被“阻隔”,因此條件獨立性質成立。

條件獨立性包含三種：成對、區域性、全域性馬爾可夫性。

成對馬爾可夫性（最大團的由來）：

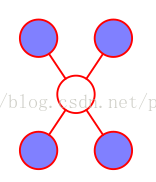
                   設u和v是無向圖G中任意兩個沒有邊連線的節點，節點u和v分別對應隨機變數Yu和Yv。其他所有節點為O，對應的隨機變數是Yo。成對馬爾可夫性是指給定隨機變數組Yo的條件下隨機變數Yu和Yv是條件獨立的，即

                            P(Yu,Yv|Yo) = P(Yu|Yo)P(Yv|Yo)

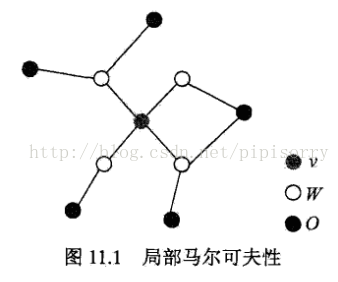
區域性馬爾可夫性（馬爾科夫毯）：

                   設v∈V是無向圖G中任意一個節點，W是與v有邊連線的所有節點，O是v、W以外的其他所有節點。v表示隨機變數是Yv，W表示的隨機變數組是YW，O表示的隨機變數組是Yo。區域性馬爾可夫性是指在給定隨機變數組YW的條件下隨機變數Yv與隨機變數組Yo是獨立的，即

                            P(Yu,Yv|Yw) = P(Yv|Yw)P(Yo|Yw)

                   在 P(Yo|YW)> 0時，等價地，  P(Yv|Yw)= P(Yv|Yw, Yo)

馬爾科夫毯：對於一個無向圖,結點 x i 的馬爾科夫毯由相鄰結點的集合組成。它的性質為:以圖中所有剩餘變數為條件, x i 的條件概率分佈只依賴於馬爾科夫毯中的變數。即結點只條件依賴於相鄰結點,而條件獨立於任何其他的結點。

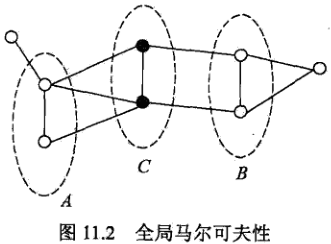
全域性馬爾可夫性：

                   設節點集合A，B是在無向圖G中被節點集合C分開的任意節點集合，如下圖所示：

                   節點集合A，B和C所對應的隨機變數組分別是YA，YB，YC。全域性馬爾可夫性是指給定隨機變數組YC條件下隨機變數組YA和YB是條件獨立的，即

                            P(YA,YB| YC) = P(YA|YC)P(YB|YC)

無向圖的分解

我們更關心如何求其聯合概率分佈。於是，為了求解給定的概率無向圖模型，我們希望將整體的聯合概率寫成若干個子聯合概率的乘積形式，也就是將概率進行因子分解，這樣便於模型的學習與計算。而事實上，概率無向圖模型的最大特點就是便於因子分解。

如果我們考慮兩個結點 x i 和 x j ,它們不存在連結,那麼給定圖中的所有其他結點,這兩個結點一定是條件獨立的。

於是,聯合概率分佈的分解一定要讓 x i 和 x j 不出現在同一個因子中,從而讓屬於這個圖的所有可能的概率分佈都滿足條件獨立性質。（lz: 成對馬爾科夫性）

團Clique和因子

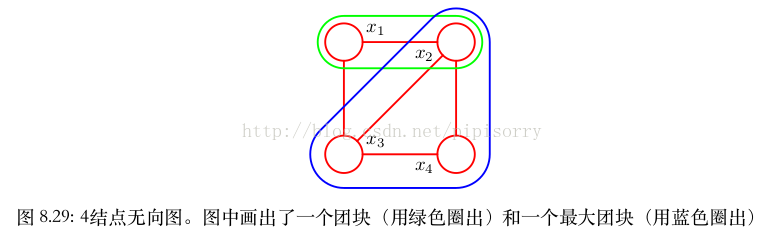
團( clique )：定義為圖中結點的一個子集,使得在這個子集中的每對結點之間都存在連結。換句話說,團塊中的結點集合是全連線的。
最大團( maximal clique )：是具有下面性質的團塊:不可能將圖中的任何一個其他的結點包含到這個團塊中而不破壞團塊的性質。

圖中有五個具有兩個結點的團塊,即 {x 1 , x 2 }, {x 2 , x 3 }, {x 3 , x 4 }, {x 4 , x 2 } 和 {x 1 , x 3 } ,還有兩個最大團塊 {x 1 , x 2 , x 3 } 和 {x 2 , x 3 , x 4 } 。集合 {x 1 , x 2 , x 3 , x 4 } 不是一個團塊,因為在 x 1 和 x 4 沒有連結。

因子：定義為團塊中變數的函式。事實上,我們可以 考 慮 最 大 團 塊 的 函 數 而 不 失 一 般 性, 因 為 其 他 團 塊 一 定 是 最 大 團 塊 的 子 集。 因 此, 如果 {x 1 , x 2 , x 3 } 是一個最大團塊,並我們在這個團塊上定義了任意一個函式,那麼定義在這些變數的一個子集上的其他因子都是冗餘的。

Hammersley-Clifford定理

概率無向圖模型的聯合概率分佈P(Y)可以表示為如下形式：

其中，C是無向圖的最大團，YC是C的節點對應的隨機變數，ΨC(YC)是C上定義的嚴格正函式，乘積是在無向圖所有的最大團上進行的。

說明：

讓我們將團塊記作 C ,將團塊中的變數的集合記作 x C 。這樣,聯合概率分佈可以寫成圖的最大團塊的勢函式( potential function ) ψ C (x C ) 的乘積的形式。通過只考慮滿足 ψ C (x C ) ≥ 0 的勢函式,我們確保了 p(x) ≥ 0 。

這裡, Z 有時被稱為劃分函式( partition function ),是一個歸一化常數,等於

由於我們的勢函式被限制為嚴格大於零,因此將勢函式表示為指數的形式更方便,即

其中 E(x C ) 被稱為能量函式( energy function )，指數表示被稱為玻爾茲曼分佈( Boltzmann distribution )。聯合概率分佈被定義為勢函式的乘積,因此總的能量可以通過將每個最大團塊的能量相加的方法得到。（lz Πexp = exp(Σ)）

如何選擇勢函式？可以這樣做:將勢函式看成一種度量,它表示了局部變數的哪種配置優於其他的配置。具有相對高概率的全域性配置對於各個團塊的勢函式的影響進行了很好的平衡。我們現在通過一個具體的例子來說明無向圖的用處。

某小皮

<br>

馬爾可夫網（條件隨機場）在計算機視覺中的應用

影象去噪、去模糊、三維重建、物體識別。

物體識別（影象分割）

[概率圖模型]

影象去噪

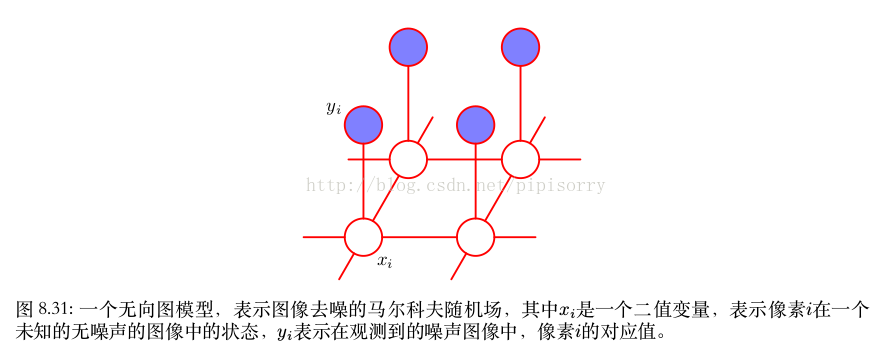
令觀測的噪聲影象通過一個二值畫素值 y i ∈ {−1, +1} 組成的陣列來描述,其中下標 i = 1, . . . , D 覆蓋了所有的畫素。我們假設影象通過下面的方式獲得:取一張未知的無噪聲影象,這幅影象由二值畫素值 x i ∈ {−1, +1} 描述,然後以一個較小的概率隨機翻轉畫素值的符號。

由於噪聲等級比較小,因此我們知道 x i 和 y i 之間有著強烈的相關性。我們還知道影象中相鄰畫素 x i 和 x j 的相關性很強。這種先驗知識可以使用馬爾科夫隨機場模型進行描述,它的無向圖如圖8.31所示。

圖中兩種型別的團塊

形如 {x i , y i } 的團塊有一個關聯的能量函式,表達了這些變數之間的相關性。對於這些團塊,我們選擇一個非常簡單的能量函式 −ηx i y i ,其中 η 是一個正的常數。這個能量函式的效果是:當 x i 和 y i 符號相同時,能量函式會給出一個較低的能量(即,較高的概率),而當 x i 和 y i 符號相反時,能量函式會給出一個較高的能量。

（lz CRF t特徵）由變數 {x i , x j } 組成的團塊,其中 i 和 j 是相鄰畫素的下標。與之前一樣,我們希望當兩 個 像 素 符 號 相 同 時 能 量 較 低, 當 兩 個 像 素 符 號 相 反 時 能 量 較 高, 因 此 我 們 選 擇 能 量 函式 −βx i x j ,其中 β 是一個正的常數。

（lz CRF s特徵）我們可以為無噪聲影象的每個畫素 i 加上一個額外的項 hx i 。這樣的項具有下面的效果:將模型進行偏置,使得模型傾向於選擇一個特定的符號,而不選擇另一個符號。

模型的完整的能量函式的形式為

Note: 令 h = 0 意味著兩個狀態 x i 的先驗概率是相等的。令 β = 0 ,從而去除了相鄰畫素點之間的聯絡,那麼整體概率最大的解為 x i = y i (對於所有的 i ),這對應於觀測到的噪聲影象。

 x 和 y 的聯合概率分佈,形式為

迭代條件峰值( iterated conditionalmodes, ICM)

( Kittler and Föglein, 1984 ) 為了恢復影象,我們希望找到一個具有較高概率(理想情況下具有最高概率)的影象 x 。

思想是,首先初始化變數 {x i } ,這個過程中我們只是簡單地令 x i = y i 對於所有 i 都成立。然後,我們每次取一個 x j 結點,計算兩個可能狀態 x j = +1 和 x j = −1 的總能量,保持其他所有結點變數固定,將 x j 設定為能量較低的狀態。如果 x j 不變,則概率不變,否則概率就會增大。由於只有一個變數發生改變,因此這是一個可以高效進行的簡單區域性計算。然後,我們對其他的結點重複更新過程,以此類推,知道滿足某個合適的停止條件。結點可以用一種系統的方式更新,例如重複地依次掃描影象,或者隨機地選擇結點。如果我們有一個更新的順序,使得每個畫素都至少被訪問一次,且沒有變數發生改變,那麼根據定義,演算法會收斂於概率的一個區域性最大值。

更加高效的演算法尋找高概率的解,這種演算法被稱為最大加和演算法,它通常會產生更好的解,雖然這種演算法仍然不保證找到後驗概率的全域性最大值。

基於圖割( graph cut )的高效的演算法,保證找到全域性的最大值( Greig et al., 1989; Boykov et al., 2001; Kolmogorov and Zabih, 2004 )。

from: http://blog.csdn.net/pipisorry/article/details/78396503

條件概率模型：https://blog.csdn.net/zxyhhjs2017/article/details/82970268

--------------------- 本文來自 -柚子皮- 的CSDN 部落格 ，全文地址請點選：https://blog.csdn.net/pipisorry/article/details/78396503?utm_source=copy