在MCMC之蒙特卡羅方法之中，講到如何利用蒙特卡羅方法來隨機模擬求解一些複雜的連續積分或者離散求和方法。但蒙特卡羅方法需要得到對應的概率分佈的樣本集，而對於某些概率分佈，得到這樣的樣本集很困難，因此本篇我們將介紹馬爾可夫鏈來解決這種問題。

1.馬爾可夫鏈簡介

馬爾可夫鏈定義比較簡單，它假設某一時刻狀態轉移的概率只依賴於它的前一個狀態，這樣可以很大程度上簡化模型的複雜度。假設我們的序列狀態為 $\mathrm{.}\mathrm{.}\mathrm{.}$

, X t − 2 , X t

− 1 , X t , X t

+ 1 , . . . ...,X_{t-2},X_{t-1},X_t,X_{t+1},... ，那麼我們在時刻 $X_{t+1}$狀態的條件概率僅僅依賴於 $X_t$，即
$P(X_{t+1}|...,X_{t-2},X_{t-1},X_t) = P(X_{t+1}|X_t)$
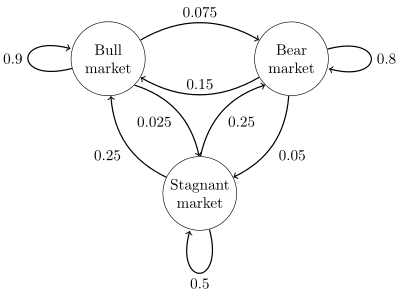
因為某一時刻狀態轉移只依賴於它的前一個狀態，那麼我們只要能求出系統中任意兩個狀態之間的轉移概率，進而得到狀態轉移概率矩陣，那麼馬爾科夫鏈的模型便定了。以下圖股市模型為例，共有三個狀態，分別為牛市(Bull market)、熊市(Bear market)、橫盤(Stagnant market)。每一個狀態都能夠以一定概率轉移到下一狀態，比如牛市以0.075的概率轉移到橫盤的概率，這些狀態轉移概率圖可以轉換為矩陣的形式進行表示。

如果我們定義矩陣 $P$某一位置 $P(i,j)$的值為 $P(j|i)$，即從狀態i轉移到狀態j的概率，並定義牛市的狀態為0、熊市狀態為1、橫盤狀態為2，這樣便得到馬爾可夫鏈模型的狀態轉移矩陣。
$\begin{bmatrix} 0.9 & 0.075 & 0.025 \\ 0.15 & 0.8 & 0.05 \\ 0.25 & 0.25 & 0.5 \end{bmatrix}$
那麼馬爾科夫鏈模型的狀態轉移矩陣和蒙特卡羅方法所需要的概率分佈樣本集有什麼關係呢？

2.馬爾可夫鏈狀態轉移矩陣性質

得到馬爾可夫鏈狀態轉移矩陣，我們看看馬爾可夫鏈模型狀態轉移矩陣的性質。仍以上面的狀態轉移矩陣為例，假設當前股市的概率分佈為[0.3, 0.4, 0.3]，即30%概率的牛市、40%概率的熊市、30%概率的橫盤。如果以這個狀態作為序列概率分佈的初始狀態t0，與狀態轉移矩陣計算得到t1,t2,t3,…時刻的概率，相應程式碼和結果如下。

import numpy as np


def markov_chain():
    matrix = np.matrix([[0.9, 0.075, 0.025], [0.15, 0.8, 0.05],
                        [0.25, 0.25, 0.5]], dtype=float)
    current = np.matrix([[0.3, 0.4, 0.3]], dtype=float)
    for i in range(100):
        current = current * matrix
        print "Current round:", i + 1
        print current


if __name__ == '__main__':
    markov_chain()

Current round: 1
[[0.405  0.4175 0.1775]]
Current round: 2
[[0.4715  0.40875 0.11975]]
Current round: 3
[[0.5156 0.3923 0.0921]]
Current round: 4
[[0.54591  0.375535 0.078555]]
...
...
Current round: 58
[[0.62499999 0.31250001 0.0625    ]]
Current round: 59
[[0.62499999 0.3125     0.0625    ]]
Current round: 60
[[0.625  0.3125 0.0625]]
Current round: 61
[[0.625  0.3125 0.0625]]
Current round: 62
[[0.625  0.3125 0.0625]]
...
...
Current round: 98
[[0.625  0.3125 0.0625]]
Current round: 99
[[0.625  0.3125 0.0625]]
Current round: 100
[[0.625  0.3125 0.0625]]

可以發現從第60輪開始，狀態轉移矩陣的概率分佈就不變了，一直保持在[0.625, 0.3125, 0.0625]，即62.5%的概率的牛市、31.25%概率的熊市、6.25%概率的橫盤，那麼這個是巧合嗎？

答案並不是巧合，如果我們換一個初始概率分佈t0，比如以[0.7, 0.1, 0.2]作為初始概率分佈，然後帶入狀態轉移矩陣得到t1,t2,t3,…時刻的概率，會發現得到同樣的結果。即最終的狀態概率分佈會趨於同一個穩定概率分佈[0.625, 0.3125, 0.0625]，也就是說，馬爾可夫鏈的狀態轉移矩陣收斂到穩定概率分佈與初始狀態概率分佈無關。

上述結果是一個非常好的形式，比如我們得到了穩定概率分佈所對應的馬爾可夫鏈模型的狀態轉移矩陣，那麼可以用任意的概率分佈樣本開始，帶入馬爾可夫鏈狀態轉移矩陣，然後就可以得到符合對應穩定概率分佈的樣本。這個性質不光對於上面的狀態轉移矩陣有效，對於絕大多數的其他馬爾可夫鏈模型的狀態轉移矩陣也有效。同時不光是離散狀態，連續狀態情況下也成立。

同時，對於一個確定的狀態轉移矩陣 $P$，它的n次冪 $P^n$也是可以確定的。同樣以上述矩陣為例，程式碼和結果如下所示。可以發現，在n>6時， $P^n$的值穩定不在變化，而且每一行都為[0.625, 0.3125, 0.0625]，這和前面提到的穩定分佈形式是一樣的。同樣這個性質不光在離散狀態下成立，連續狀態時也成立。

import numpy as np


def markov_chain():
    matrix = np.matrix([[0.9, 0.075, 0.025], [0.15, 0.8, 0.05], [0.25, 0.25, 0.5]], dtype=float)
    for i in range(10):
        matrix = matrix * matrix
        print "Current round:", i + 1
        print matrix


if __name__ == '__main__':
    markov_chain()

Current round: 1
[[0.8275  0.13375 0.03875]
 [0.2675  0.66375 0.06875]
 [0.3875  0.34375 0.26875]]
Current round: 2
[[0.73555  0.212775 0.051675]
 [0.42555  0.499975 0.074475]
 [0.51675  0.372375 0.110875]]
...
Current round: 5
[[0.62502532 0.31247685 0.06249783]
 [0.6249537  0.31254233 0.06250397]
 [0.62497828 0.31251986 0.06250186]]
Current round: 6
[[0.625  0.3125 0.0625]
 [0.625  0.3125 0.0625]
 [0.625  0.3125 0.0625]]
...
Current round: 10
[[0.625  0.3125 0.0625]
 [0.625  0.3125 0.0625]
 [0.625  0.3125 0.0625]]

下面用數學語言總結下馬爾可夫鏈的收斂性質，如果一個非週期的馬爾可夫鏈有狀態轉移矩陣P，並且他的任意兩個狀態是連通的，那麼 $lim_{n \rightarrow \infty} P_{ij}^n$與i無關。我們可以得到

$lim_{n \rightarrow \infty} P_{ij}^n = \pi (j)$

$lim_{n \rightarrow \infty} P ^n = \begin{bmatrix} \pi(1) & \pi(2) & ... & \pi(j) & ...\\ \pi(1) & \pi(2) & ... & \pi(j) & ...\\ \pi(1) & \pi(2) & ... & \pi(j) & ...\\ \pi(1) & \pi(2) & ... & \pi(j) & ...\\ \pi(1) & \pi(2) & ... & \pi(j) & ...\\ \end{bmatrix}$