1015 - 計算幾何之直線與直線的關係 - Intersecting Lines(POJ1269)
阿新 • • 發佈:2018-11-10
題意
給你兩條直線
若其相交則輸出 交點的座標
若其平行則輸出 NONE
若其重合則輸出 LINE
分析
比較基礎的計算幾何,就是考向量的使用
判斷兩條直線是否平行,就是看其叉積是否為0(可以這樣理解,兩個向量的叉積的集合意義就是平行四邊形的面積,當你兩條直線平行的時候,面積自然為0)
進一步如何判斷是否重合呢?只需要在判斷平行的基礎上再看兩條直線中是否有一個端點位於另一條直線上即可
相交的時候輸出其交點也很好辦,利用好叉積的性質
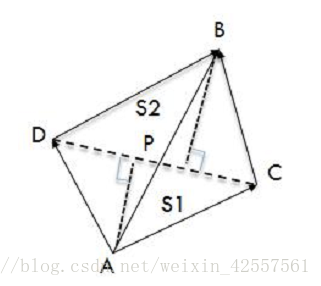
計算出S1和S2,然後利用比值關係,對向量AB進行放縮,就可以得到交點P的座標了
程式碼
#include<cstdio> #include<cstring> #include<iostream> #include<cmath> using namespace std; const double eps=1e-7; struct point{ double x,y; point (double _x=0.0,double _y=0.0):x(_x),y(_y){} friend inline point operator +(const point &a,const point &b){ return point(a.x+b.x,a.y+b.y); } friend inline point operator -(const point &a,const point &b){ return point(a.x-b.x,a.y-b.y); } friend inline point operator *(double k,const point &a){ return point(k*a.x,k*a.y); } friend inline double dot(const point &a,const point &b){ return (a.x*b.x+a.y*b.y); } friend inline double cross(const point &a,const point &b){ return (a.x*b.y-b.x*a.y); } friend inline double len(const point &a){ return sqrt(dot(a,a)); } friend inline double dis (const point &a,const point &b){ return len(a-b); }//向量常見的運算 }a[5]; int n,m; bool on(const point &a,const point &b,const point &c){ int det=cross(a-c,b-c); if(det!=0) return 0; return 1; } int main(){ scanf("%d",&n); printf("INTERSECTING LINES OUTPUT\n"); int i,j,k; for(i=1;i<=n;++i){ for(j=1;j<=4;++j) scanf("%lf%lf",&a[j].x,&a[j].y); double det=cross(a[2]-a[1],a[4]-a[3]); if(det==0){ if(on(a[3],a[4],a[1])) {printf("LINE\n");continue;} printf("NONE\n"); } else{ double S1=cross(a[3]-a[1],a[3]-a[4]),S2=cross(a[3]-a[4],a[3]-a[2]); double k=S1/(S1+S2); point c=k*(a[2]-a[1]); printf("POINT %.2f %.2f\n",a[1].x+c.x,a[1].y+c.y); } } printf("END OF OUTPUT"); return 0; }