Scrambled Polygon

Time Limit: 1000MS Memory Limit: 30000K

Total Submissions: 6513 Accepted: 3092

Description
A closed polygon is a figure bounded by a finite number of line segments. The intersections of the bounding line segments are called the vertices of the polygon. When one starts at any vertex of a closed polygon and traverses each bounding line segment exactly once, one comes back to the starting vertex.

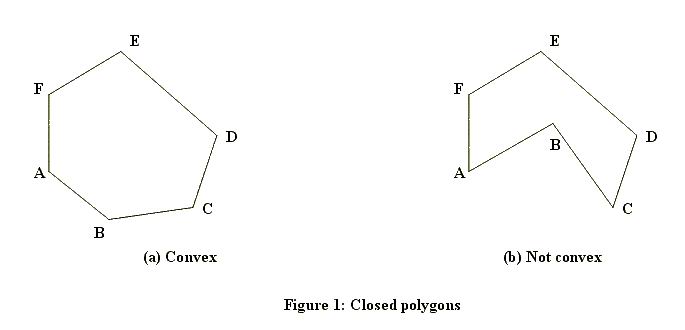
A closed polygon is called convex if the line segment joining any two points of the polygon lies in the polygon. Figure 1 shows a closed polygon which is convex and one which is not convex. (Informally, a closed polygon is convex if its border doesn't have any "dents".)


The subject of this problem is a closed convex polygon in the coordinate plane, one of whose vertices is the origin (x = 0, y = 0). Figure 2 shows an example. Such a polygon will have two properties significant for this problem.

The first property is that the vertices of the polygon will be confined to three or fewer of the four quadrants of the coordinate plane. In the example shown in Figure 2, none of the vertices are in the second quadrant (where x < 0, y > 0).

To describe the second property, suppose you "take a trip" around the polygon: start at (0, 0), visit all other vertices exactly once, and arrive at (0, 0). As you visit each vertex (other than (0, 0)), draw the diagonal that connects the current vertex with (0, 0), and calculate the slope of this diagonal. Then, within each quadrant, the slopes of these diagonals will form a decreasing or increasing sequence of numbers, i.e., they will be sorted. Figure 3 illustrates this point.


Input
The input lists the vertices of a closed convex polygon in the plane. The number of lines in the input will be at least three but no more than 50. Each line contains the x and y coordinates of one vertex. Each x and y coordinate is an integer in the range -999..999. The vertex on the first line of the input file will be the origin, i.e., x = 0 and y = 0. Otherwise, the vertices may be in a scrambled order. Except for the origin, no vertex will be on the x-axis or the y-axis. No three vertices are colinear.

Output

The output lists the vertices of the given polygon, one vertex per line. Each vertex from the input appears exactly once in the output. The origin (0,0) is the vertex on the first line of the output. The order of vertices in the output will determine a trip taken along the polygon's border, in the counterclockwise direction. The output format for each vertex is (x,y) as shown below.

Sample Input
0 0
70 -50
60 30
-30 -50
80 20
50 -60
90 -20
-30 -40
-10 -60

90 10

Sample Output
(0,0)
(-30,-40)
(-30,-50)
(-10,-60)
(50,-60)
(70,-50)
(90,-20)
(90,10)
(80,20)

(60,30)

計算幾何，給出一系列點，按照極角排序。

應該屬於Graham求凸包的前置題目吧。。。

很基礎。注意輸入時判定停止。

在注意一下精度，應該就OK了，

說一下極角排序幾種方法吧，這些都是看人家Blog。

1.利用叉積的正負來作cmp.(即是按逆時針排序).此題就是用這種方法

double cross(point p0,point p1,point p2)
{
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
// sort排序函式
bool cmp(const point &a, const point &b)//逆時針排序
{
    point origin;
    // 設定原點
    origin.x = origin.y = 0;
    return cross(origin,b,a)<EPS;
}

2.利用complex的內建函式。

#include<complex>
#define x real()
#define y imag()
#include<algorithm>
using namespace std;

bool cmp(const Point& p1, const Point& p2)
{
    return arg(p1) < arg(p2);
}

3.利用arctan計算極角大小。（範圍『-180，180』）

bool cmp(const Point& p1, const Point& p2)
{     
    return atan2(p1.y, p1.x) < atan2(p2.y, p2.x);
}

4.利用象限加上極角，叉積。

bool cmp(const point &a, const point &b)//先按象限排序，再按極角排序，再按遠近排序 
{
    if (a.y == 0 && b.y == 0 && a.x*b.x <= 0)return a.x>b.x;
    if (a.y == 0 && a.x >= 0 && b.y != 0)return true;
    if (b.y == 0 && b.x >= 0 && a.y != 0)return false;
    if (b.y*a.y <= 0)return a.y>b.y;
    point one;
    one.y = one.x = 0;
    return cross(one,a,one,b) > 0 || (cross(one,a,one,b) == 0 && a.x < b.x);    
}

恩，就是這些啦~

/**************************************
***************************************
*        Author：Tree                 *
*From  ：http://blog.csdn.net/lttree  *
* Title : Scrambled Polygon           *
*Source: poj 2007                     *
* Hint  : 凸包                        *
***************************************
**************************************/
#include <stdio.h>
#include <algorithm>
#include <iostream>
using namespace std;
#define EPS 1e-8
struct point
{
    double x,y;
}p[51];

double cross(point p0,point p1,point p2)
{
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
// sort排序函式
bool cmp(const point &a, const point &b)//逆時針排序
{
    point origin;
    // 設定原點
    origin.x = origin.y = 0;
    return cross(origin,b,a)<EPS;
}
int main()
{
    int i,n;
    n=0;
    while( scanf("%lf%lf",&p[n].x,&p[n].y)!=EOF )
    {
        ++n;
    }
    // 極角排序，第一個空過去
    sort(p+1,p+n,cmp);

    for(i=0;i<n;++i)
        printf("(%.0lf,%.0lf)\n",p[i].x,p[i].y);

    return 0;
}