此處對比批量梯度下降、隨機梯度下降、小批量梯度下降演算法的優缺點

演算法	批量梯度下降（Batch Gradient Descent, BGD）	隨機梯度下降（Stochastic Gradient Descent, SGD）
代價函式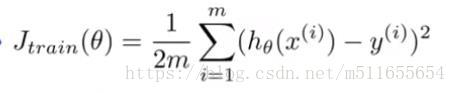
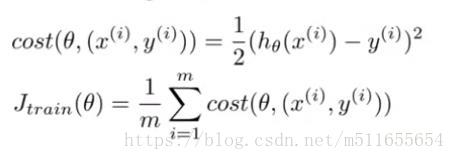梯度下降演算法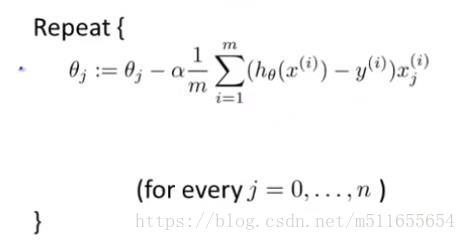
比較	每一次更新引數θ時，都需要計算所有m個訓練樣本的差平方項求和，然後更新一次θ值，當m很大時，每一次迭代計算量大，且只能更新優化一小步	每一次更新引數θ時，不需要對所有m個訓練樣本的差平方項求和，只需要計算當前一個訓練樣本，然後更新一次θ，每一次迭代只要保證對一個樣本擬合很好就行了
優點	引數基本以直線式方向朝著全域性最小值的方向更新，最終達到收斂	每次迭代只需使用一個訓練樣本，當m很大時，訓練速度快，計算量小
缺點	每次迭代都需要用到m個訓練樣本，當m很大時，訓練速度慢，計算成本高	一般來講，引數朝著全域性最小值的方向更新，但也不一定，會以某個比較隨機的、迂迴的路徑朝全域性最小值逼近，並在最小值點附近徘徊，並非直接逼近最小值點並停留在該點上，但這也基本滿足了我們實際應用的目的了

演算法	小批量梯度下降（Mini-Batch Gradient Descent）
代價函式	此處，m=b
梯度下降演算法
比較	每一次更新引數θ時，需要計算b個訓練樣本，然後更新一次θ，每一次迭代只要保證對b個樣本擬合很好就行了
優點	每次迭代都需要用到b個訓練樣本（通常b=10，變化範圍在2-100之間），演算法介於BGD和SGD之間，當m很大時，當擁有一個很好的向量化實現時（能夠支援平行計算），有時速度比SGD更快
缺點	增加了一個額外引數b，需要花時間確定引數b的大小

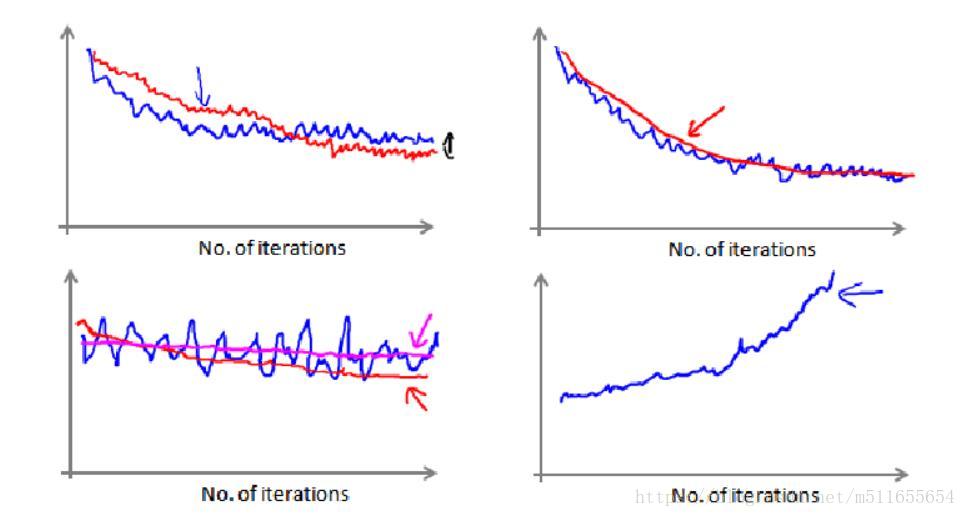
當SGD在全域性最小值點附近振盪時，通過除錯演算法、選取學習率α來繪製圖表，監測梯度下降是否收斂。

在隨機梯度下降中，我們在每一次更新 θ 之前都計算一次代價，然後每 x 次迭代後，求出這 x 次對訓練例項計算代價的平均值，然後繪製這些平均值與 x 次迭代的次數之間的函式圖表。 

當我們繪製這樣的圖表時，可能會得到一個顛簸不平但是不會明顯減少的函式影象（如上面左下圖中藍線所示）。我們可以增加 α 來使得函式更加平緩，也許便能看出下降的趨勢了（如上面左下圖中紅線所示）；或者可能函式圖表仍然是顛簸不平且不下降的（如洋紅色線所示），那麼我們的模型本身可能存在一些錯誤。 

通常學習速度α是不變的，但可以通過修改α（在逼近全域性最小值點時，α減小）的方式來收斂到全域性最小值點。

隨著不斷地靠近全域性最小值，通過減小學習率，我們迫使演算法收斂而非在最小值附近徘徊。但是通常我們不需要這樣做便能有非常好的效果了，對α進行調整所耗費的計算通常不值得 。

總結：

這種方法不需要定時地掃描整個訓練集，來算出整個樣本集的代價函式，而是隻需要每次對最後 1000 個，或者多少個樣本，求一下平均值。應用這種方法，你既可以保證隨機梯度下降法正在正常運轉和收斂，也可以用它來調整學習速率 α 的大小。