Liang-Barsky演算法

在Cohen-Sutherland演算法提出後，樑友棟和Barsky又針對標準矩形視窗提出了更快的Liang-Barsky直線段裁剪演算法。

樑演算法的主要思想：

（1）用引數方程表示一條直線

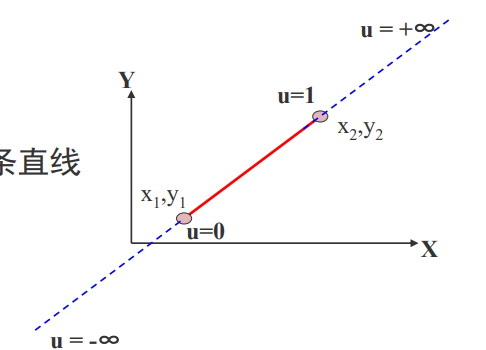
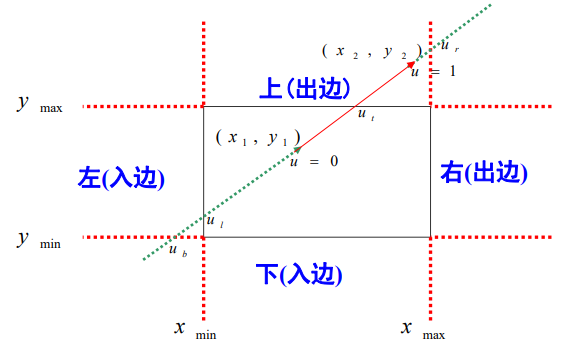
（2）把被裁剪的紅色直線段看 成是一條有方向的線段，把視窗 的四條邊分成兩類：

入邊和出邊

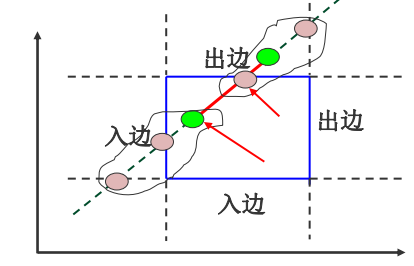
裁剪結果的線段起點是直線和兩條入邊的交點以及始端點三 個點裡最前面的一個點，即引數u最大的那個點；

裁剪線段的終點是和兩條出邊的交點以及端點最後面的一個 點，取引數u最小的那個點。

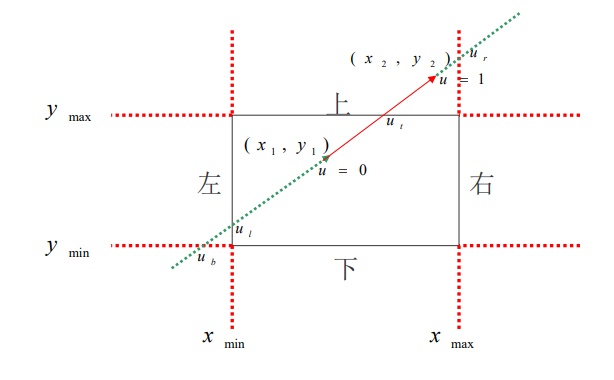
值得注意的是，當u從-∞到+∞遍歷直線時，首先對裁剪視窗的兩條邊界直線（下邊和左邊）從外面向裡面移動，

再對裁 剪視窗兩條邊界直線（上邊和右邊）從裡面向外面移動。

如果用u1，u2分別表示 線段（u1≤u2）可見部分的開始和結束

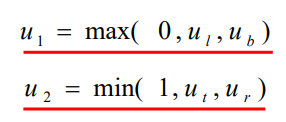
Liang-Barsky演算法的基本出發點是直線的引數方程

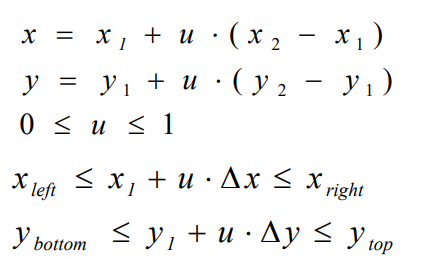
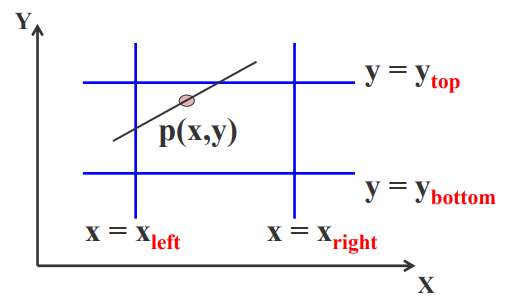
（1）分析Pk=0的情況

如果還滿足qk<0

則線段完全在邊界外，應舍 棄該線段

如果qk≥0

則進一步判斷

（2）當pk≠0時：

當pk<0時

線段從裁剪邊界延長線的外部 延伸到內部，是入邊交點

當pk > 0時

線段從裁剪邊界延長線的內部 延伸到外部，是出邊交點

線段和視窗邊界一共有四個交點，根據pk的符號，就知道 哪兩個是入交點，哪兩個是出交點

當p k < 0時：對應入邊交點

當p k > 0時：對應出邊交點

一共四個u值，再加上u=0、u=1兩個端點值，總共六個值

把pk＜0的兩個u值和0比較去找最大的，把pk＞0的兩個u值 和1比較去找最小的，這樣就得到兩個端點的引數值