Liang-Barsky直線段裁剪演算法
引數化演算法(Cyrus-Beck)
考慮凸多邊形區域R和直線段P1P2:P(t)=(P2-P1)*t+P1
設A是區域R的邊界上一點,N是區域邊界在A點的內法線向量
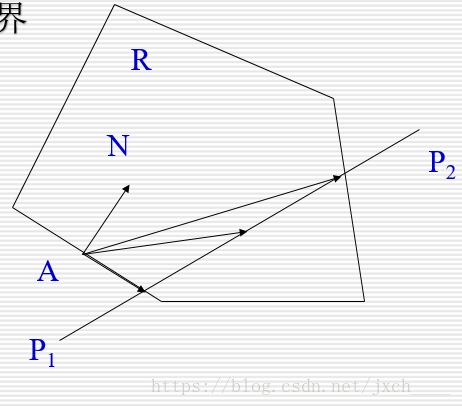
則對於線段P1P2上任一點P(t)
N ·(P(t)-A)< 0
外側
N ·(P(t)-A)>0
內側
N ·(P(t)-A)=0
凸多邊形的性質:點P(t)在凸多邊形內的充要條件是,對於凸多邊形邊界上任意一點A和該點處內法向N,都有N·(P(t)-A)>0
k條邊的多邊形,可見線段引數區間的解:
Ni· (p(t)-Ai)>=0, i=0,…,k, 0≤t ≤1.
即:Ni· (P1-Ai)+ Ni· (P2-P1) t>=0

令ti= Ni· (P1-Ai)/[Ni· (P2-P1) ]
Ni· (P2-P1) =0-> 平行於對應邊。
此時判斷Ni· (P1-Ai)
若Ni· (P1-Ai) <0
若Ni· (P1-Ai) >0
P1 P2在多邊形內側->繼續其它邊的判斷
對於t值的選擇:首先,要符合0≤t≤1;其次,對於凸視窗來說,每一個線段與其至多有兩個交點,即有兩個相應的t值。所以我們可以把計算出的t值分成兩組:一組為下限組,是分佈線上段起點一側的;一組為上限組,是分佈線上段終點一側的。這樣,只要找出下限組中的最大值及上限組中的最小值,就可確定線段了。
分組的依據是:
如果Ni· (P2-P1) <0,則計算出的值屬於上限組
如果Ni· (P2-P1) >0,則計算出的值屬於下限組
引數化演算法的幾何意義
上限組以Ni· (P2-P1) <0為特徵,表示在該處沿P1P2方向前進將越來越遠地離開多邊形區域。
下限組以Ni· (P2-P1) >0為特徵,表示在該處沿P1P2方向前進將接近或進入多邊形內側。
因此,線段可見的交點引數:
tl=max{0,max{ti: Ni· (P2-P1) >0}}
tu=min{1,min{ti: Ni· (P2-P1)<0}}
若 tl <= tu, [tl , tu]是可見線段的交點引數區間,否則,線段不可見。
當凸多邊形是矩形視窗且矩形的邊與座標軸平行時,該演算法退化為Liang-Barsky演算法。


