動態規劃-揹包問題(跳躍點解法)
對於 0-1 揹包問題,DP的解法很普遍。還有一種“跳躍點”的解法,該方法的提出,是根據揹包求解過程中的記錄表 v(i,j)的函式性特點而來的。(v(i,j)表記錄的是前 i 種物品,達到總重量 j 時的最大利益)
可以Dp 求解一下,然後列印一下表進行觀察,也可以根據這個求解原理,可以很自然的想到,v(i,j)的函值, 當 i 確定時,這是一個關於 j 的非遞減函式,且由“跳躍點”將函式分段兒了,類似於上取整/下取整的函式影象,以跳躍點為分界非遞減的一段一段兒“平”的函式影象。在求解過程中,每一個 i 都會有對應著一個這樣的函式影象,並且最後一個求解時,剛好,最高的跳躍點對應的函式線即為解。
根據 v(i,j) = max(v(i-1,j) , v(i-1,j-w[i])+v[i]),即對於一個函式影象 v(i)是可以有其“前驅” v(i-1)得出的。求解過程是 由前導後的,並且根據公式,本質上,新的跳躍點,新的函式影象就是在已有影象的基礎上得出的(即 i 狀態本身就是在 i-1 的狀態下得出的)。實際求解過程 :(過程中需要打表記錄,表中的資料記錄是一個structure,即佔用 w 時最大價值為 v,過程中以 i (前 i 種物品為狀態標記量))
1.初始化 p(0)<0 , 0 > // 邊界
2.由 p(i-1)[ v ( i -1 , j ) 的狀態圖 ] 得到 q(i-1)[ v ( i - 1 , j - w[i] ) + v[i] 的狀態圖 ] . 只需要在 p(i-1)的基礎上 + (wi,vi)得到新的跳躍點即可。
3. p(i-1)並上 q(i-1)在減去必然不合法的點(同 w 下 v 非最大的點)即為 p(i)
上述即為求解過程,迭代實現即可。
程式碼在實際實現的過程中,把一維表 table 用作了 二維表,通過 head[ ] 陣列的劃分,達到了二維表的效果,head[ i ] 表示 p(i)在表中的首元素位置(這樣來區分不同的i對應的資料,相當於行標記)。同時藉助 p(i-1)導 p(i)的時候,用 l ,r 作為指標,卡在了p(i-1)的左右作為邊界,next是p(i)要填寫的位置,最初時 next 為 p(i)的head 位置。
圖示:

先在 p(i-1)的元素 j 上得到一個新狀態,然後 w 小於它的不受影響,直接搬,w 等於它的,對 v 取大更,w 大於它的,根據 v 值直接pass 掉 不合法的點(w 大但 v 小於前邊的),同時,出現了新狀態往裡寫的時候,也要注意,w 大 v 也大時才合法,才可以往裡寫,反之直接扔掉。(在跳躍點函式影象中,保留的的是 max ,即p(i-1),q(i-1)倆函式圖取 max 的合圖)
記錄好表之後,從終態開始往回倒找解路徑即可。
程式碼如下:
1 // knapSack.cpp: 定義控制檯應用程式的入口點。
2 //
3
4 #include "stdafx.h"
5 // 動態規劃 揹包問題 跳躍點優化
6 #include<stack>
7 #include<minmax.h>
8 #include<iostream>
9 using namespace std;
10
11 const int N = 1e4, M = 1e6;
12
13 struct Data
14 {
15 int w, v;
16 Data(int nw = 0, int nv = 0) :w(nw), v(nv) {}//建構函式,預設w,v都為0
17 Data operator +(const Data& r)const//設計data結構體的+操作
18 {
19 return Data(w + r.w, v + r.v);
20 }
21
22 bool operator ==(const Data& r)const//設計data結構體的==操作
23 {
24 return (w == r.w) && (v == r.v);
25 }
26 };
27
28 int head[N + 5];//標記每一個i的表的首元素,相當於將一維陣列轉換為二維陣列
29 Data goods[N], table[M];//goods[]儲存物品資訊,table[i]儲存對應裝前i個物品對應的(w,v)
30 stack<int> numlist;//存放最終放入物品序號的棧
31 int n, c;//物品數量和揹包總容量
32
33 // trace back to find the solution vector x[1……n]
34 void traceBack(Data eState)
35 {//eState是最後一個i的表的最後一個數據信息
36 int i, j;
37 bool x[N + 2];
38 for (i = n; i >= 1; --i)
39 {
40 x[i] = false;
41 for (j = head[i] - 1; j >= head[i - 1]; --j)//從p[i-1]的末尾遍歷到p[i-1]的開頭
42 {
43 if (table[j] + goods[i] == eState && (table[j].w != 0 || !j))
44 {//這裡判斷有沒有加入第i個物品,若加入,則將i序號進棧,並且將對應i-1的表的最好的資料賦值給estate進行回溯
45 numlist.push(i);
46 //cout << i << ",";//測試進棧情況
47 eState = table[j];
48 break;
49 }
50 }
51 }
52 }
53
54 // jump points' method to slove the 0-1 bag's problem
55 int GKnapSack()
56 {
57 int i, k, j, boundaryL, boundaryR, next;//boundaryL, boundaryR作為指標,卡在p[i-1]的左右為邊界,next是p[i]要填寫的位置,初始時next為
58 //p[i]的首位置,k依次往後移動,直到到達p[i-1]的右邊界
59 Data temp;
60
61 head[0] = 0;//p[0]的首位置為索引0
62 table[0] = Data(0, 0);//沒有裝物品時各項資料都為0
63 boundaryL = boundaryR = 0;
64 next = 1;//p[1]要填寫的位置即索引1
65 head[1] = 1;//p[i]的首位置為1
66 for (i = 1; i <= n; ++i)
67 {
68 k = boundaryL;//數字k在處理中從p[i-1]的左邊界移動到右邊界
69 for (j = boundaryL; j <= boundaryR; ++j)
70 {
71 if (table[j].w + goods[i].w > c)
72 break;
73 /*先在 p(i-1)的元素 j 上得到一個新狀態,然後 w 小於它的不受影響,直接搬*/
74 temp = table[j] + goods[i];//將p[i-1]對應的列表中的移動到的資料的容量和價值分別加上第i件物品的容量和價值
75 while (k <= boundaryR && table[k].w)
76 {//next是p[i]要填寫的位置,初始時next為p[i]的首位置,依次往後移動,
77 //直到到達p[i-1]的右邊界
78 table[next] = table[k];
79 ++next;
80 ++k;
81 }
82 /*w 等於它的,對 v 取更大的值*/
83 if (k <= boundaryR && table[k].w == temp.w)
84 {
85 temp.v = max(temp.v, table[k].v);//如果容量相同,則取價值最大的
86 ++k;
87 }
88 /*w 大於它的,根據 v 值直接pass 掉 不合法的點(w 大但 v 小於前邊的)*/
89 if (temp.v > table[next - 1].v)
90 {
91 table[next] = temp;
92 ++next;
93 }
94 while (k <= boundaryR && table[k].v <= table[next - 1].v)
95 ++k;
96 }
97 while (k <= boundaryR)
98 {
99 table[next] = table[k];
100 ++next;
101 ++k;
102 }
103
104 boundaryL = boundaryR + 1;//boundaryL指向p[i]的左邊界,即下一個i對應的表的左邊界,因為此時p[i]的表已經填好,要利用i標記來藉助p[i]匯出p[i+1]
105 boundaryR = next - 1;//因為next指向p[i+1]的首位置的索引,所以boundaryR指向next-1,即得到p[i]的右邊界
106 head[i + 1] = next;
107 }
108
109 traceBack(table[next - 1]);
110
111 return table[next - 1].v;
112 }
113
114 int main()
115 {
116 int i;
117 cout << "請輸入揹包的總數量和總容量" << endl;
118 cin >> n;
119 cin >> c;
120 cout << "請分別輸入每個揹包的重量和價值" << endl;
121 for (i = 1; i <= n; ++i)
122 {
123 cin >> goods[i].w;
124 cin >> goods[i].v;
125 }
126 cout << "結果最大價值是:" << GKnapSack() << endl;
127 cout << "該例項的重量價值表:" << endl;
128 for (i = 0; i <= n; ++i)
129 {
130 cout << i << ":";
131 for (int j = head[i]; j < head[i + 1]; ++j)
132 {
133 cout << table[j].w << "," << table[j].v << ";";
134 }
135 cout << endl;
136 }
137
138 cout << endl;
139 cout << "裝入的物品序號是:" << endl;
140 while (!numlist.empty())
141 {
142 cout << numlist.top() << ",";
143 numlist.pop();
144 }
145 cout << endl;
146 return 0;
147 }
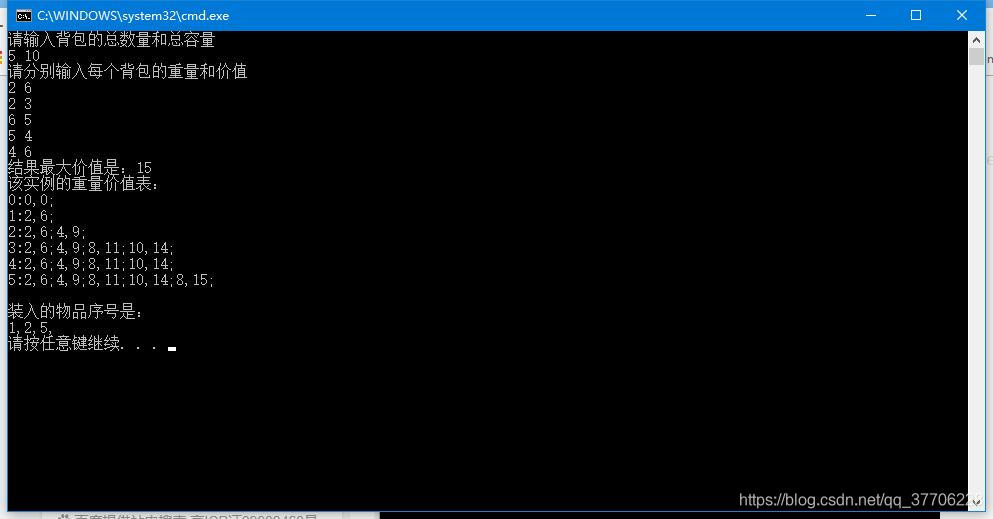
結果截圖:
參考文章:
