支援向量機-引入及原理
阿新 • • 發佈:2018-11-10
支援向量機(Support Vector Machines, SVM):是一種監督學習演算法。處理二分類
- 支援向量(Support Vector)就是離分隔超平面最近的那些點。
- 機(Machine)就是表示一種演算法,而不是表示機器。
線性可分資料集:將資料集分隔開的直線稱為分隔超平面。我們希望找到離分隔超平面最近的點,確保它們離分隔面的距離儘可能遠,這裡點到分隔面的距離被稱為間隔(margin)。
線性不可分資料集:利用核函式(kernel)將資料對映到高維,轉化成線性可分
支援向量機 場景
- 要給左右兩邊的點進行分類
- 明顯發現:選擇D會比B、C分隔的效果要好很多。

尋找最大間隔
分隔超平面是一條直線,點到超平面的距離 == 點到直線的距離
點到直線的距離公式
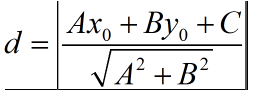
理論推導(李航的統計學習方法):

定義拉格朗日函式:


將目標函式有極大轉換成求極小,就得到下面與之等價的對偶最優化問題

但是幾乎所有資料都不那麼“乾淨”,引入鬆弛變數,允許資料點可以處於分隔面的錯誤一側
此時新的約束條件則變為:
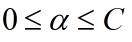
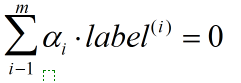
總的來說:
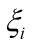 表示鬆弛變數
表示鬆弛變數
常量C是 懲罰因子, 表示離群點的權重(用於控制“最大化間隔”和“保證大部分點的函式間隔小於1.0” )
- C值越大,表示離群點影響越大,就越容易過度擬合;反之有可能欠擬合。
- 我們看到,目標函式控制了離群點的數目和程度,使大部分樣本點仍然遵守限制條件。
- 例如:正類有10000個樣本,而負類只給了100個(C越大表示100個負樣本的影響越大,就會出現過度擬合,所以C決定了負樣本對模型擬合程度的影響!,C就是一個非常關鍵的優化點!)
SVM中的主要工作就是要求解 alpha.
