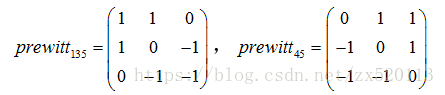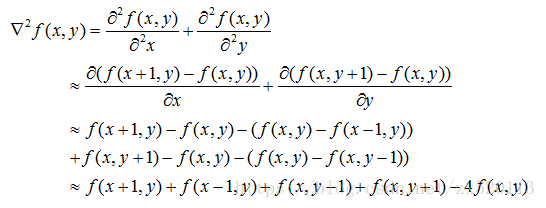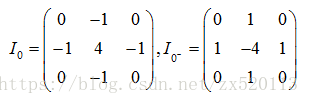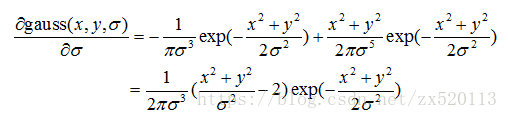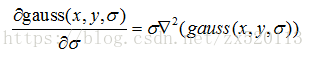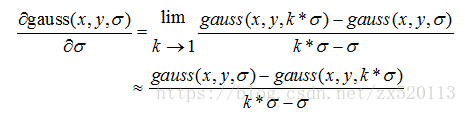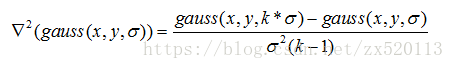8、邊緣檢測

      大多數邊緣檢測運算元是基於方向差分卷積核求卷積的方法，通常有四種方式來衡量最後輸出的邊緣強度。（1）取對應位置絕對值的和：    ，（2）取對應位置平方和的開方：，（3）取對應位置絕對值的最大值：，（4）插值法： 。

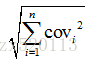
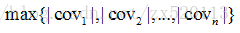
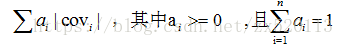
      Roberts運算元卷積核：

      Prewitt運算元卷積核：

      Sobel運算元卷積核：

      Sobel運算元是在一個座標軸方向上進行非歸一化的高斯平滑，在另一個座標軸方向上進行差分處理。n*n的Sobel運算元是由高斯平滑運算元和差分運算元Full卷積而得到的。

      Scharr運算元卷積核有水平方向、垂直方向、45度方向、135度方向，和Prewitt運算元的卷積核類似，但在數字上變成了3,10,3。

      Kirsch運算元：影象與每一個核進行卷積，然後去絕對值作為對應方向上的邊緣強度的量化，對8個卷積結果去絕對值，然後在對應位置取最大值作為最後輸出的邊緣強度，超過255進行截斷。

      Robinson運算元和Kirsch運算元一樣。

      通過np.array()構建卷積核，通過signal.convolve2d()對影象和卷積核進行卷積計算。

      在邊緣檢測中常用的邊緣檢測運算元是Canny運算元、Laplacian運算元、高斯差分邊緣檢測、Marr-Hildreth邊緣檢測。下面將對以上四種邊緣檢測的演算法實現進行簡單的過程思路介紹。

      Canny邊緣檢測

      Canny運算元在Sobel運算元、Prewitt等運算元沒有充分利用邊緣的梯度方向，最後輸出的二值圖只是簡單的利用閾值進行處理，如果閾值過大會損失很多邊緣資訊，如果閾值過小會出現噪聲。針對這兩個缺點，Canny運算元進行了改進，基於邊緣梯度方形的非極大值抑制，雙閾值的滯後閾值處理。

      Canny邊緣檢測演算法實現思想如下：

      （1）影象分別於Sobel運算元的水平方向和垂直方向上的卷積核卷積得到dx和dy（畫素點大小有正負），然後利用平方和的開方得到邊緣強度。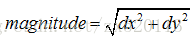

      （2）利用dx和dy計算出梯度方向，angle=arctan2(dy,dx)，即對每一個位置（r，c），angle(r,c)=arctan2(dy(r,c),dx(r,c))代表該位置的梯度方向，一般用角度表示，即angle(r,c)在[0,180]和[-180,0]之間。

      通過angle=np.arctan2(dy,dx)/np.pi*180計算梯度方向。

      （3）對每一個位置進行非極大值抑制的處理，非極大值抑制操作返回的仍然是一個矩陣。在邊緣強度影象magnitude，判斷magnitude(r,c)左邊點的梯度方向angle(r,c)=arctan2(dy(r,c),dx(r,c))，根據該梯度方向在該點繪製一條斜線，比較該點的畫素值與斜線穿過該點的“右上方和左下方”的畫素值的大小進行比較，如果magnitude(r,c)大於這兩個點的值，則成為極大值，否則為非極大值。

      （4）雙閾值的滯後閾值處理，經過第三步的非極大值抑制處理後的邊緣強度圖，一般需要閾值化處理，常用的方法是全域性閾值分割和區域性自適應閾值分割。這裡用到的滯後閾值處理設定了兩個閾值，高閾值和低閾值。邊緣強度大於高閾值的那些店作為確定的邊緣點；邊緣強度低於低閾值的那些點立即被剔除；邊緣強度在低閾值和高閾值之間的那些點，按照只有這些點能按某一路徑與確定邊緣點相連線時，才可以作為邊緣點被接受。

      Laplacian邊緣檢測

      二維函式f(x,y)的Laplacian變換，

      將其推廣到離散的二維陣列（矩陣），即矩陣的拉普拉斯變換是矩陣與拉普拉斯核的卷積。

      影象矩陣與拉普拉斯核的卷積本質上是計算任意位置上的值與其水平方向和垂直方向上四個相鄰點平均值之間的差值。拉普拉斯的缺點對噪聲產生較大的影響，誤將噪聲作為邊緣；優點只有一個卷積核，其計算成本比其他運算元低。拉普拉斯其他常用形式的運算元如下：

      拉普拉斯核內所有值得和必須等於0，這樣就使得在恆等灰度值區域不會產生錯誤的邊緣，上述幾種形式的拉普拉斯運算元是不可分離的。

      高斯拉普拉斯邊緣檢測

      對二維高斯函式：

      進行拉普拉斯變換：

      Python語言的LOG卷積核構建：

    H,W=size

    r,c=np.mgrid[0:5:1,0:5:1]

    r-=(H-1)/2

    c-=(W-1)/2

    sigma2=pow(sigma,2.0)

    norm2=np.power(r,2.0)+np.power(c,2.0)

    LoGKernel=(norm2/sigma2-2)*np.exp(-norm2/(2*sigma2))

      最後對高斯拉普拉斯後的結果進行二值化處理。

      高斯差分邊緣檢測

      二維高斯函式：

      對σ進行一階偏導如下：

      其和高斯拉普拉斯有如下關係：

      根據一階導數的定義，二維高斯函式對σ進行一階偏導可以這樣表示：

      根據上面兩個公式，可以得到高斯拉普拉斯的近似值：

      當k=0.95時，高斯拉普拉斯核高斯差分的近似值相等。

      最後對高斯差分後的結果進行二值化處理。

      高斯卷積gauss(x，y,σ)：

    H,W=size

    xr,xc=np.mgrid[0:1,0:W]

    xc-=(W-1)/2

    xk=np.exp(-np.power(xc,2.0))

    I_xk=signal.convolve2d(I,xk,’same’,’symm’)

    yr,yc=np.mgrid[0:H,0:1]

    yr-=(H-1)/2

    yk=np.exp(-np.power(yr,2.0))

    I_xk_yk=signal.convolve2d(I_xk,yk,’same’,’symn’)

    I_xk_yk*=1.0/(2*np.pi*pow(sigma,2.0))

      Marr-Hildreth邊緣檢測

      Marr-Hildreth邊緣檢測只是將高斯差分和高斯拉普拉斯檢測最後一步的閾值化處理改成尋找過零點位置的操作。過零點操作，對於函式f(x)，求一階導數，其一階導數的最大值點就是其二階導數的零點位置，使得二階導數等於0，也就是邊緣強度最大值處。

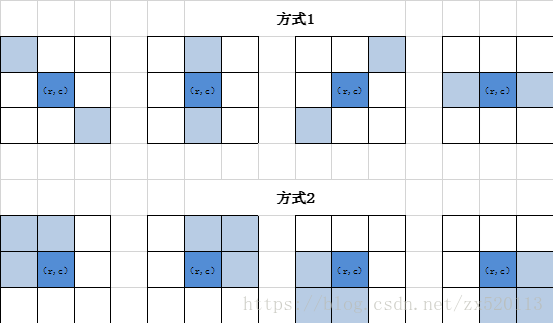
      一般通過以下兩種方式來尋找過零點：

      方式1中，對於這四種情況只要有一種情況出現異號，該位置（r,c）就是過零點，即為邊緣點，即將該位置的輸出標記為白色，通過兩個位置的畫素點相乘來判斷是否是異號。

      方式2中，對於這四個領域的均值，只要任意兩個均值是異號，該位置（r,c）就是過零點，即為邊緣點，將該位置的輸出值設為白色，首先利用mean函式來計算每個區域的均值，然後通過判斷min(fourmean)*max(fourmean)是否異號來判斷是否是邊緣點。