2. 程式人生 > >資料結構之最短路徑

資料結構之最短路徑

阿新 • • 發佈：2018-11-11

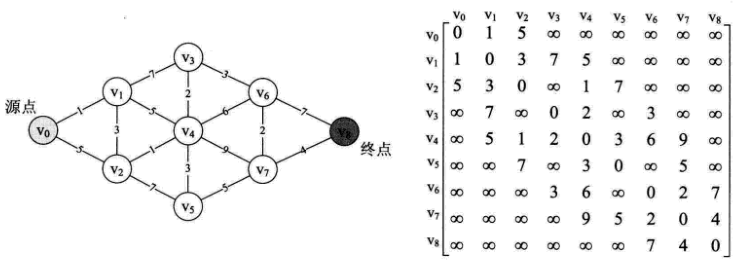
對於網圖來說，最短路徑，是指兩頂點之間經過的邊上權值之和最少的路徑，並且我們稱路徑上的第一個頂點是源點，最後一個頂點是終點。

迪傑斯特拉（Dijkstra）演算法

這是一個按路徑長度遞增的次序產生最短路徑的演算法。它的思路大體是這樣的：並不是一下子就求出v0到v8的最短路徑，而是一步步求出它們之間頂點的最短路徑，過程中都是基於已經求出的最短路徑的基礎上，求得更遠頂點的最短路徑，最終得到你要的結果。
在這裡插入圖片描述

#include "stdio.h"    
#include "stdlib.h"   
#include "io.h"  
#include "math.h"  
#include
 
 "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXEDGE 20
#define MAXVEX 20
#define INFINITY 65535
typedef int Status;	/* Status是函式的型別,其值是函式結果狀態程式碼，如OK等 */
typedef struct
{
	int vexs[MAXVEX];
	int arc[MAXVEX][MAXVEX];
	int numVertexes, numEdges;
}MGraph;
typedef int Patharc[
 
MAXVEX];    /* 用於儲存最短路徑下標的陣列 */
typedef int ShortPathTable[MAXVEX];/* 用於儲存到各點最短路徑的權值和 */

								   /* 構件圖 */
void CreateMGraph(MGraph *G)
{
	int i, j;
	/* printf("請輸入邊數和頂點數:"); */
	G->numEdges = 16;
	G->numVertexes = 9;
	for (i = 0; i < G->numVertexes; i++)/* 初始化圖 */
	{
		G->vexs[i] = i;
	}
	for
 
 (i = 0; i < G->numVertexes; i++)/* 初始化圖 */
	{
		for (j = 0; j < G->numVertexes; j++)
		{
			if (i == j)
				G->arc[i][j] = 0;
			else
				G->arc[i][j] = G->arc[j][i] = INFINITY;
		}
	}
	G->arc[0][1] = 1;
	G->arc[0][2] = 5;
	G->arc[1][2] = 3;
	G->arc[1][3] = 7;
	G->arc[1][4] = 5;
	G->arc[2][4] = 1;
	G->arc[2][5] = 7;
	G->arc[3][4] = 2;
	G->arc[3][6] = 3;
	G->arc[4][5] = 3;
	G->arc[4][6] = 6;
	G->arc[4][7] = 9;
	G->arc[5][7] = 5;
	G->arc[6][7] = 2;
	G->arc[6][8] = 7;
	G->arc[7][8] = 4;
	for (i = 0; i < G->numVertexes; i++)
	{
		for (j = i; j < G->numVertexes; j++)
		{
			G->arc[j][i] = G->arc[i][j];
		}
	}

}
/*  Dijkstra演算法，求有向網G的v0頂點到其餘頂點v的最短路徑P[v]及帶權長度D[v] */
/*  P[v]的值為前驅頂點下標,D[v]表示v0到v的最短路徑長度和 */
void ShortestPath_Dijkstra(MGraph G, int v0, Patharc *P, ShortPathTable *D)
{
	int v, w, k, min;
	int final[MAXVEX];/* final[w]=1表示求得頂點v0至vw的最短路徑 */
	for (v = 0; v<G.numVertexes; v++)    /* 初始化資料 */
	{
		final[v] = 0;			/* 全部頂點初始化為未知最短路徑狀態 */
		(*D)[v] = G.arc[v0][v];/* 將與v0點有連線的頂點加上權值 */
		(*P)[v] = -1;				/* 初始化路徑陣列P為-1  */
	}
	(*D)[v0] = 0;  /* v0至v0路徑為0 */
	final[v0] = 1;    /* v0至v0不需要求路徑 */
					  /* 開始主迴圈，每次求得v0到某個v頂點的最短路徑 */
	for (v = 1; v<G.numVertexes; v++)
	{
		min = INFINITY;    /* 當前所知離v0頂點的最近距離 */
		for (w = 0; w<G.numVertexes; w++) /* 尋找離v0最近的頂點 */
		{
			if (!final[w] && (*D)[w]<min)
			{
				k = w;
				min = (*D)[w];    /* w頂點離v0頂點更近 */
			}
		}
		final[k] = 1;    /* 將目前找到的最近的頂點置為1 */
		for (w = 0; w<G.numVertexes; w++) /* 修正當前最短路徑及距離 */
		{
			/* 如果經過v頂點的路徑比現在這條路徑的長度短的話 */
			if (!final[w] && (min + G.arc[k][w]<(*D)[w]))
			{ /*  說明找到了更短的路徑，修改D[w]和P[w] */
				(*D)[w] = min + G.arc[k][w];  /* 修改當前路徑長度 */
				(*P)[w] = k;
			}
		}
	}
}
int main(void)
{
	int i, j, v0;
	MGraph G;
	Patharc P;
	ShortPathTable D; /* 求某點到其餘各點的最短路徑 */
	v0 = 0;
	CreateMGraph(&G);
	ShortestPath_Dijkstra(G, v0, &P, &D);
	printf("最短路徑倒序如下:\n");
	for (i = 1; i<G.numVertexes; ++i)
	{
		printf("v%d - v%d : ", v0, i);
		j = i;
		while (P[j] != -1)
		{
			printf("%d ", P[j]);
			j = P[j];
		}
		printf("\n");
	}
	printf("\n源點到各頂點的最短路徑長度為:\n");
	for (i = 1; i<G.numVertexes; ++i)
		printf("v%d - v%d : %d \n", G.vexs[0], G.vexs[i], D[i]);
	system("pause");
	return 0;
}

執行結果為：

最短路徑倒序如下:
v0 - v1 :
v0 - v2 : 1
v0 - v3 : 4 2 1
v0 - v4 : 2 1
v0 - v5 : 4 2 1
v0 - v6 : 3 4 2 1
v0 - v7 : 6 3 4 2 1
v0 - v8 : 7 6 3 4 2 1
源點到各頂點的最短路徑長度為:
v0 - v1 : 1
v0 - v2 : 4
v0 - v3 : 7
v0 - v4 : 5
v0 - v5 : 8
v0 - v6 : 10
v0 - v7 : 12
v0 - v8 : 16

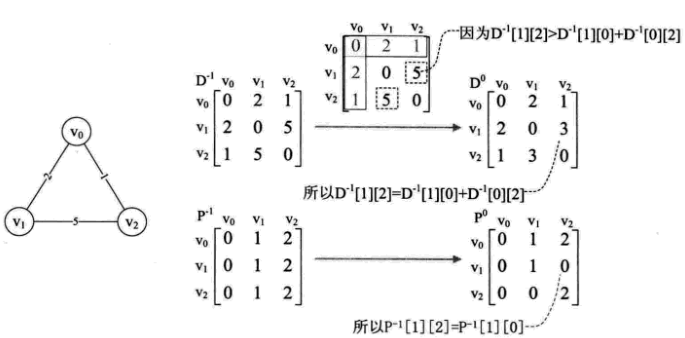
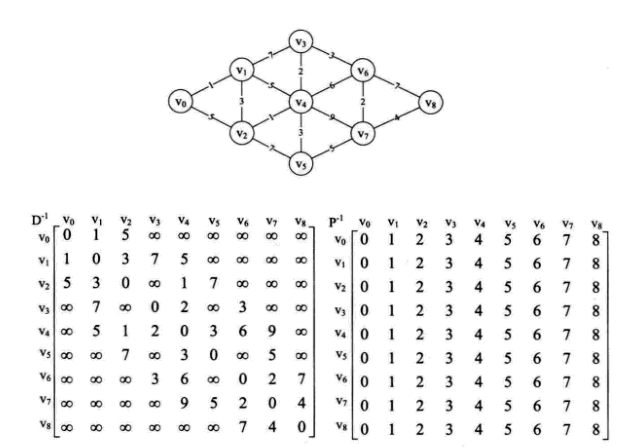
弗洛伊德（Floyd）演算法

先定義兩個二維陣列 D [ 3 ] [ 3 ] D[3][3] 和 P [ 3 ] [ 3 ] P[3][3] ， D D 代表頂點到頂點的最短路徑權值和的矩陣，初始化為 D − 1 D^{-1} ，其實就是初始的圖的鄰接矩陣。將 P P 命名為 P − 1 P^{-1} ，初始化為圖中矩陣。
在這裡插入圖片描述

首先分析所有的頂點經過v0後到達另一個頂點的最短路徑。因為只有三個頂點，因此需要檢視v1->v0->v2，得到路徑為3。而v1->v2權值為5，所以就有了 D 0 D^0 矩陣，同時修改 P 0 P^0 矩陣。接下來，再在 D 0 和 P 0 D^0和P^0 的基礎上計算經過v1和v2的後到達另一個頂點的最短路徑，得到 D 1 、 P 1 和 D 2 、 P 2 D^1、P^1和D^2、P^2 。
在這裡插入圖片描述

#include "stdio.h"    
#include "stdlib.h"   
#include "io.h"  
#include "math.h"  
#include "time.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXEDGE 20
#define MAXVEX 20
#define INFINITY 65535

typedef int Status;	/* Status是函式的型別,其值是函式結果狀態程式碼，如OK等 */

typedef struct
{
	int vexs[MAXVEX];
	int arc[MAXVEX][MAXVEX];
	int numVertexes, numEdges;
}MGraph;

typedef int Patharc[MAXVEX][MAXVEX];
typedef int ShortPathTable[MAXVEX][MAXVEX];

/* 構件圖 */
void CreateMGraph(MGraph *G)
{
	int i, j;

	/* printf("請輸入邊數和頂點數:"); */
	G->numEdges = 16;
	G->numVertexes = 9;

	for (i = 0; i < G->numVertexes; i++)/* 初始化圖 */
	{
		G->vexs[i] = i;
	}

	for (i = 0; i < G->numVertexes; i++)/* 初始化圖 */
	{
		for (j = 0; j < G->numVertexes; j++)
		{
			if (i == j)
				G->arc[i][j] = 0;
			else
				G->arc[i][j] = G->arc[j][i] = INFINITY;
		}
	}

	G->arc[0][1] = 1;
	G->arc[0][2] = 5;
	G->arc[1][2] = 3;
	G->arc[1][3] = 7;
	G->arc[1][4] = 5;

	G->arc[2][4] = 1;
	G->arc[2][5] = 7;
	G->arc[3][4] = 2;
	G->arc[3][6] = 3;
	G->arc[4][5] = 3;

	G->arc[4][6] = 6;
	G->arc[4][7] = 9;
	G->arc[5][7] = 5;
	G->arc[6][7] = 2;
	G->arc[6][8] = 7;

	G->arc[7][8] = 4;


	for (i = 0; i < G->numVertexes; i++)
	{
		for (j = i; j < G->numVertexes; j++)
		{
			G->arc[j][i] = G->arc[i][j];
		}
	}

}

/* Floyd演算法，求網圖G中各頂點v到其餘頂點w的最短路徑P[v][w]及帶權長度D[v][w]。 */
void ShortestPath_Floyd(MGraph G, Patharc *P, ShortPathTable *D)
{
	int v, w, k;
	for (v = 0; v<G.numVertexes; ++v) /* 初始化D與P */
	{
		for (w = 0; w<G.numVertexes; ++w)
		{
			(*D)[v][w] = G.arc[v][w];	/* D[v][w]值即為對應點間的權值 */
			(*P)[v][w] = w;				/* 初始化P */
		}
	}
	for (k = 0; k<G.numVertexes; ++k)
	{
		for (v = 0; v<G.numVertexes; ++v)
		{
			for (w = 0; w<G.numVertexes; ++w)
			{
				if ((*D)[v][w]>(*D)[v][k] + (*D)[k][w])
				{/* 如果經過下標為k頂點路徑比原兩點間路徑更短 */
					(*D)[v][w] = (*D)[v][k] + (*D)[k][w];/* 將當前兩點間權值設為更小的一個 */
					(*P)[v][w] = (*P)[v][k];/* 路徑設定為經過下標為k的頂點 */
				}
			}
		}
	}
}

int main(void)
{
	int v, w, k;
	MGraph G;

	Patharc P;
	ShortPathTable D; /* 求某點到其餘各點的最短路徑 */

	CreateMGraph(
            
  

           

              
              

            

            
相關推薦

			   
            
            
            
 

    


    
    
資料結構之最短路徑

     
  
 
  
  
 對於網圖來說，最短路徑，是指兩頂點之間經過的邊上權值之和最少的路徑，並且我們稱路徑上的第一個頂點是源點，最後一個頂點是終點。 
 迪傑斯特拉（Dijkstra）演算法 
 這是一個按路徑長度遞增的次序產生最短路徑的演算法。它的思路大體是這樣的：並不是一下子就求出v0到v8的最短路徑，而是 



  
 

    


    
    
資料結構之最短路徑Dijkdtra演算法

     
 

/*
 * Dijkstra最短路徑。
 * 即，統計圖(G)中"頂點vs"到其它各個頂點的最短路徑。
 *
 * 引數說明：
 *        G -- 圖
 *       vs -- 起始頂點(start vertex)。即計算"頂點vs"到其它頂點的最短路徑。
 *     prev -- 前驅 



  
 

    


    
    
Java資料結構----圖--最短路徑解法Dijkstra演算法和Floyd演算法

     
 
                
最短路徑—Dijkstra演算法和Floyd演算法
1、Dijkstra演算法
1.1、定義概覽
Dijkstra(迪傑斯特拉)演算法是典型的單源最短路徑演算法，用於計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴充套件，直到擴充套件到終點為止。Di 



  
 

    


    
    
最短路徑之最短路徑問題

     
 導入   n+2   lan   ble   一行   memset   ems   esp   php   [提交] [狀態] [討論版] [命題人:外部導入]
題目描述
    平面上有n個點（n<=100），每個點的坐標均在-10000~10000之間。其中的一些點之間有連線。     若有連線， 



  
 

    


    
    
資料結構之最大子列和

     
  
 
 #include <stdlib.h>
#include <stdio.h>
int MaxSubseqSum(int a[],int N)
{
    int i,ThisSum = 0,MaxSum = 0;
   &nb 



  
 

    


    
    
資料結構之最小生成樹

     
 
                一、Prim演算法的實現

待補充、、、、

二、Kruskal演算法的實現：

#include<iostream>
#include<algorithm>
using namespace std;
#define MaxInt 32767//表示無 



  
 

    


    
    
SDUT OJ 2143 圖結構練習——最短路徑

     
 
								
								            
						
                


圖結構練習——最短路徑




Time Limit: 1000MS Memory limit: 65536K


題目描述

 給定一個帶權無向圖，求節點1到節點n的最短路徑。




輸入

 



  
 

    


    
    
圖結構練習——最短路徑（Dijkstra演算法）

     
 
							
							
							think: 
1注意重複邊的覆蓋 
2注意map陣列的初始化 
3注意dist陣列的初始化



圖結構練習——最短路徑 
Time Limit: 1000MS Memory Limit: 65536KB

Problem Description 
 給定一個 



  
 

    


    
    
poj 1273 最大流之最短路徑增廣法（EK）

     
 
                


Drainage Ditches

Time Limit: 1000MS

Memory Limit: 10000K
Total Submissions: 71182

Accepted: 27694


Description

Every time it rains 



  
 

    


    
    
貪心演算法之最短路徑問題（Dijkstra演算法）

     
 
                
1、問題
一個求單源最短路徑的問題。給定有向帶權圖 G =(V, E ),
其中每條邊的權是非負實數。此外,給定 V 中的一個頂點,
稱為源點。現在要計算從源到所有其他各頂點的最短路徑長
度,這裡路徑長度指路上各邊的權之和。


2、分析




3、程式碼實現
1、普通C 



  
 

    


    
    
SDUT 2143 圖結構練習——最短路徑

     
 
                


//Flyod
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;

int Edge[10010][10010];

int main()
{
    int n, m; 



  
 

    


    
    
圖結構練習——最短路徑（Dijkstra）

     
 
                圖結構練習——最短路徑

Time Limit: 1000 ms Memory Limit: 65536 KiB



Problem Description

 給定一個帶權無向圖，求節點1到節點n的最短路徑。



Input

 輸入包含多組資料，格式如下。

第一行包 



  
 

    


    
    
圖之最短路徑

     
 
							
							
							    目前求最短路徑的演算法很多，下面2種是基本不再使用，但卻是經典的路徑演算法。其他路徑演算法有啟發式演算法A*,D*,還有樹形的RRT, RRT*等。

1. Dijkstra演算法

    a. 基本思想：求帶權有向圖中某個源點到其他各頂點的最短路徑， 



  
 

    


    
    
**圖結構練習——最短路徑**

     
 
							
							
							圖結構練習——最短路徑 
Time Limit: 1000 ms Memory Limit: 65536 KiB

Problem Description 
 給定一個帶權無向圖，求節點1到節點n的最短路徑。

Input 
 輸入包含多組資料，格式如下。 
第 



  
 

    


    
    
資料結構基礎之圖（下）：最短路徑

     
  
 
 轉自：http://www.cnblogs.com/edisonchou/p/4691020.html 
   
 圖（下）：最短路徑 
 圖的最重要的應用之一就是在交通運輸和通訊網路中尋找最短路徑。例如在交通網路中經常會遇到這樣的問題：兩地之間是否有公路可通；在有多條公路可通的情況下，哪 



  
 

    


    
    
資料結構與演算法--最短路徑之Floyd演算法

     
 
                

  一、解決單源最短路徑問題的Dijkstra演算法     

我們知道Dijkstra演算法只能解決單源最短路徑問題，且要求邊上的權重都是非負的。那麼有沒有辦法解決任意起點到任意頂點的最短路徑問題呢？如果用Dijkstra演算法，可以這樣做：

Dijkstra[]  



  
 

    


    
    
資料結構之（圖最短路徑之）Dijkstra(迪傑斯特拉)演算法

     
 
                
1）常用的圖最短路徑的演算法有兩個：Dijkstra演算法和Floyd演算法；
2）Dijkstra演算法適用於求圖中兩節點之間最短路徑，Floyd演算法適於求圖中任意兩節點間；
3）兩種演算法的主要思想是動態規劃，而Dijkstra演算法設計比較巧妙的是：在求源節點到終結 



  
 

    


    
    
資料結構圖之三-----------最短路徑

     
 

最短路徑？別亂想哈，其實就是字面意思，一個帶邊值的圖中從某一個頂點到另外一個頂點的最短路徑。

官方定義：對於內網圖而言，最短路徑是指兩頂點之間經過的邊上權值之和最小的路徑。

並且我們稱路徑上的第一個頂點為源點，最後一個頂點為終點。

由於非內網圖沒有邊上的權值，所謂的最短路徑其實是指兩頂點之間經過的邊 



  
 

    


    
    
資料結構圖之三（最短路徑--迪傑斯特拉演算法）

     
 
  1 #include <iostream>
  2 #include "SeqList.h"
  3 #include "Stack.h"
  4 #include <iomanip>
  5 using namespace std;
  6 
  7 #defin 



  
 

    


    
    
資料結構之（圖最短路徑之）Floyd（弗洛伊德）演算法

     
 
                
1）弗洛伊德演算法是求圖最短路徑的另外一種演算法，其適用於求圖中任意兩節點之間最短路徑；
2）其基本思想也是動態規劃，時間複雜度是O(N^3),N代表節點個數；
3）動態規劃的實現步驟是：a）找出問題的最優子結構；b）根據最優子結構求出遞迴解；c）以自下而上的方式求出最優解