時間序列演算法

time series data mining 主要包括decompose（分析資料的各個成分，例如趨勢，週期性），prediction（預測未來的值），classification（對有序資料序列的feature提取與分類），clustering（相似數列聚類）等。

時間序列的預測

常用的思路：

1、計算平均值

2、exponential smoothing指數衰減

   不同的時間點，賦予不同的權重，越接近權重越高

3、snaive：假設已知資料的週期，上一個週期對應的值作為下一個週期的預測值

4、drift：飄移，即用最後一個點的值加上資料的平均趨勢

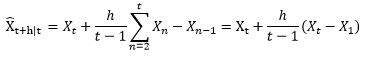
5、Holt-Winters：  三階指數平滑

 Holt-Winters的思想是把資料分解成三個成分：平均水平（level），趨勢（trend），週期性（seasonality）。R裡面一個簡單的函式stl就可以把原始資料進行分解：

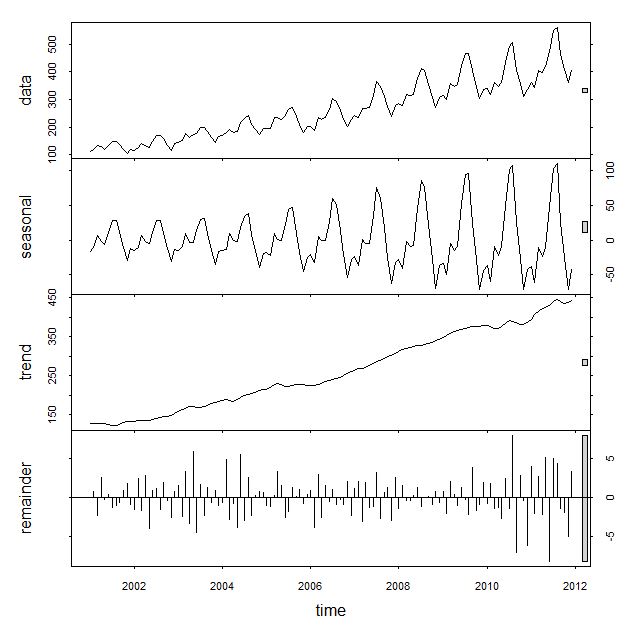
一階Holt—Winters假設資料是stationary的（靜態分佈），即是普通的指數平滑。

二階演算法假設資料有一個趨勢，這個趨勢可以是加性的(additive,線性趨勢)，也可以是乘性的(multiplicative,非線性趨勢)，只是公式裡面一個小小的不同而已。 

三階演算法在二階的假設基礎上，多了一個週期性的成分。同樣這個週期性成分可以是additive和multiplicative的。 舉個例子，如果每個二月的人數都比往年增加1000人，這就是additive；如果每個二月的人數都比往年增加120%，那麼就是multiplicative。

效能衡量採用的是RMSE。 當然也可以採用別的metrics：

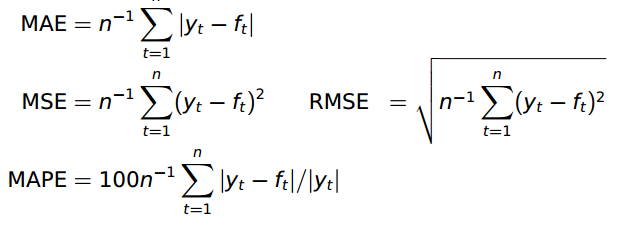
6、ARIMA： AutoRegressive Integrated Moving Average，ARIMA是兩個演算法的結合：AR和MA。在ARMA模型中，AR代表自迴歸，MA代表移動平均。其公式如下：

• 是白噪聲，均值為0， C是常數。  ARIMA的前半部分就是Autoregressive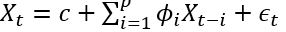：， 後半部分是moving average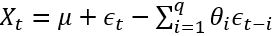： 。  AR實際上就是一個無限脈衝響應濾波器（infinite impulse resopnse）, MA是一個有限脈衝響應（finite impulse resopnse），輸入是白噪聲。

ARIMA裡面的I指Integrated（差分）。 ARIMA（p,d,q）就表示p階AR，d次差分，q階MA。

為什麼要進行差分呢？ ARIMA的前提是資料是stationary的，也就是說統計特性（mean，variance，correlation等）不會隨著時間視窗的不同而變化。用數學表示就是聯合分佈相同。

當然很多時候並不符合這個要求，例如這裡的airline passenger資料。有很多方式對原始資料進行變換可以使之stationary：

（1） 差分，即Integrated。 例如一階差分是把原數列每一項減去前一項的值。二階差分是一階差分基礎上再來一次差分。這是最推薦的做法。

（2）先用某種函式大致擬合原始資料，再用ARIMA處理剩餘量。例如，先用一條直線擬合airline passenger的趨勢，於是原始資料就變成了每個資料點離這條直線的偏移。再用ARIMA去擬合這些偏移量。

（3）對原始資料取log或者開根號。這對variance不是常數的很有效。

如何看資料是不是stationary呢？這裡就要用到兩個很常用的量了： ACF（auto correlation function）和PACF(patial auto correlation function)。對於non-stationary的資料，ACF圖不會趨向於0，或者趨向0的速度很慢。

acf(train)                                ——原始資料

acf(diff(train,lag=1))                    ——一階差分

acf(diff(diff(train,lag=7)))              ——去除週期性的一階差分

確保stationary之後，下面就要確定p和q的值了。定這兩個值還是要看ACF和PACF：

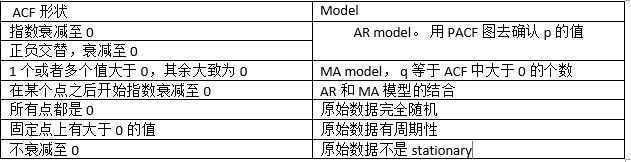
AR(p)模型，PACF會在lag=p時截尾，也就是，PACF圖中的值落入寬頻區域中。

MA(q)模型，ACF會在lag=q時截尾，同理，ACF圖中的值落入寬頻區域中。

確定好p和q之後，就可以呼叫R裡面的arime函數了。

ARIMA更多表示為  ARIMA(p,d,q)(P,D,Q)[m] 的形式，其中m指週期（例如7表示按周），p,d,q就是前面提的內容，P,D,Q是在週期性方面對應的p,d,q含義。

R裡面有兩個很強大的函式： ets 和 auto.arima。 使用者什麼都不需要做，這兩個函式會自動挑選一個最恰當的演算法去分析資料。

在R中各個演算法的效果如下：

預測效果評價：accuracy()函式包含了很多評價指標，也可以自定義。

模擬了兩個模型後，可以用AIC(mod1)來檢驗與比較，值越小越好。

 

案例：

我們有一個時間序列的資料 "D1_data.txt"

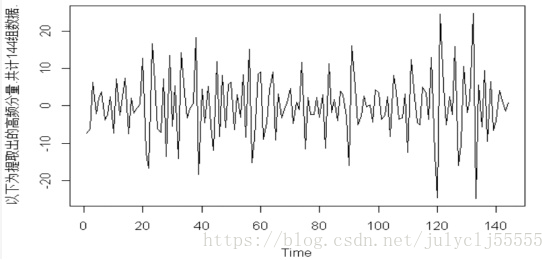
1.拿到這個時間序列你先目測，上圖通過目測可以認為是一個平穩的時間序列。

 

R步驟

a <- read.csv(“D:/D1_data.txt”) #括號中的東西取決於你的資料在電腦上存放的路徑

aa <-ts(a)  #命名該事件序列為aa

plot(aa)  #畫出時間序列aa如上圖

 

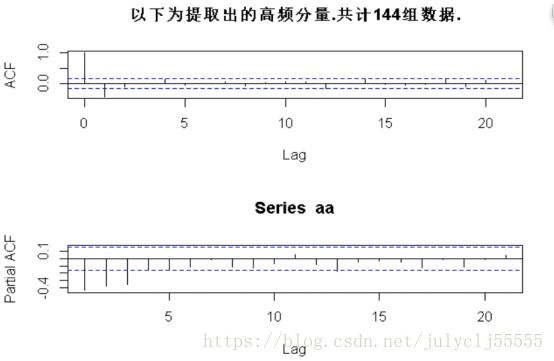
2、通過ACF和PACF也就是自相關係數和偏自相關係數來判斷是否穩定

由於ACF在lag=1之後便落入置信區間，PACF在lag=3之後落入置信區間，我們認為該時間序列穩定。

R步驟

layout(1:2)  #一次顯示兩張圖

acf(aa)  #顯示自相關係數

pacf(aa)  #顯示偏自相關係數

 

3、模型擬合

選擇ma(1)或者arma(3,1)

用arima命令來擬合，並用AIC來看哪個模型更適合，AIC數值越小越好。

R步驟

ma1 <- arima(aa,order = c(0,0,1))

arma13 <- arima(aa,order = c(3,0,1))

AIC(ma1)

AIC(arma13)

#AIC結果：

AIC(ma1) [1] 939.6636

AIC(arma13) [1] 943.8848

可以看出ma1優於arma13.

 

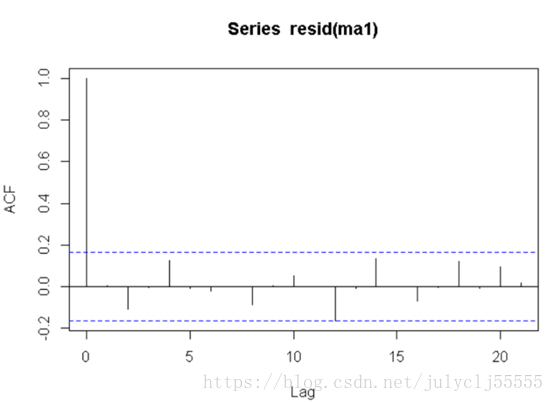
4、看擬合好的模型的殘差是否為白噪聲

R步驟

acf(resid(ma1))   #ma1的殘差的自相關係數

注意事項：

對於這幾個模型的選擇絕對不是IC誰高就選誰。

正確的流程：1）根據acf和pacf的特點進行選擇。比如題主的圖acf緩慢下行，而pacf只有一個lag significant，這樣對應的model是AR，相反如果pacf decays而acf cuts off，你就該去選MA。每個model都有對應的acf，pacf的特點，根據對應的特點細節去選model，選lag，增加sessional ar ma，驗證殘差等等。

2）在1）的基礎上選出的可能性的model中，用IC和殘差的表現來選一個最好的，這時候才用到IC。不談1）來談IC沒有意義。其中還有很多需要注意的點建議題主自己搜尋學習一下。

有trend代表一定不stationary，但這並不影響模型，在去除趨勢項後，一個時間序列依然可以穩態，這個叫做trend stationary，因此即使有trend，依然可以使用ar等模型來model。

存在趨勢的序列都是非平穩的，AR等一系列模型是必須建立在平穩的基礎上才有意義…一般時間序列建模的流程是：去除確定性因素（趨勢還有季節性），然後對剩下的隨機因素進行平穩性檢驗，檢驗通過之後進行arima建模，具體的階數你可以用acf，pacf來確定，比較方便的是R裡面的auto.arima直接定階…然後進行模型的擬合與預測…最後就是對殘差進行arch效應檢驗，如果有arch效應，就進一步用波動率模型進行建模…總的來說就是確定性因素的分解—隨機因素的均值建模—波動率建模。

疑問：

如何判斷一個序列是否平穩？

1、均值 ，是與時間t 無關的常數。

2、方差 ，是與時間t 無關的常數。這個特性叫做方差齊性。

3、協方差 ，只與時期間隔k有關，與時間t 無關的常數。

如果一個序列不平穩，就要用方法使它變平穩：如消除長期趨勢、差分化

檢查平穩性的公式，

1、引入Rho係數：X(t) = Rho * X(t-1) + Er(t)

2、Dickey-Fuller檢驗是測試一個自迴歸模型是否存在單位根。X(t) - X(t-1) = (Rho - 1) X(t - 1) + Er(t)，要測試如果Rho–1=0是否差異顯著。如果零假設不成立，我們將得到一個平穩時間序列。

 

如何判斷一個序列符合AR還是MA？

自迴歸AR案例：

例如，x(t)代表一個城市在某一天的果汁的銷售量。在冬天，極少的供應商進果汁。突然有一天，溫度上升了，果汁的需求猛增到1000.然而過了幾天，氣溫有下降了。但是眾所周知，人們在熱天會喝果汁，這些人會有50%在冷天仍然喝果汁。在接下來的幾天，這個比例降到了25%(50%的50%），然後幾天後逐漸降到一個很小的數。

移動平均MA案例：

一個公司生成某種型別的包，這個很容易理解。作為一個競爭的市場，包的銷售量從零開始增加的。所以，有一天他做了一個實驗，設計並製作了不同的包，這種包並不會被隨時購買。因此，假設市場上總需求是1000個這種包。在某一天，這個包的需求特別高，很快庫存快要完了。這天結束了還有100個包沒賣掉。我們把這個誤差成為時間點誤差。接下來的幾天仍有幾個客戶購買這種包。

AR模型與MA模型的不同

AR與MA模型的主要不同在於時間序列物件在不同時間點的相關性。

MA模型用過去各個時期的隨機干擾或預測誤差的線性組合來表達當前預測值。當n>某一個值時，x(t)與x(t-n)的相關性總為0.

AM模型僅通過時間序列變數的自身歷史觀測值來反映有關因素對預測目標的影響和作用，步驟模型變數相對獨立的假設條件約束，所構成的模型可以消除普通回退預測方法中由於自變數選擇、多重共線性等造成的困難。即AM模型中x(t)與x(t-1)的相關性隨著時間的推移變得越來越小。

用ACF和PACF來區分AR與MA

時間序列x(t)滯後k階的樣本自相關係數（ACF）和滯後k期的情況下樣本偏自相關係數（PACF）。

AR模型的ACF和PACF：

通過計算證明可知：

- AR的ACF為拖尾序列，即無論滯後期k取多大，ACF的計算值均與其1到p階滯後的自相關函式有關。

- AR的PACF為截尾序列，即當滯後期k>p時PACF=0的現象。

 

上圖藍線顯示值與0具有顯著的差異。很顯然上面PACF圖顯示截尾於第二個滯後，這意味這是一個AR（2）過程。

MA模型的ACF和PACF：

- MA的ACF為截尾序列，即當滯後期k>p時PACF=0的現象。

- AR的PACF為拖尾序列，即無論滯後期k取多大，ACF的計算值均與其1到p階滯後的自相關函式有關。

 

很顯然，上面ACF圖截尾於第二個滯後，這以為這是一個MA（2）過程

 

如何讓時間序列變得平穩？

1 消除趨勢：這裡我們簡單的刪除時間序列中的趨勢成分

2 差分：這個技術常常用來消除非平穩性。這裡我們是對序列的差分的結果建立模型而不是真正的序列。

x(t) – x(t-1) = ARMA (p , q)

差分後，ARIMA對應為：p:AR    d:I     q:MA

3 季節性：季節性直接被納入ARIMA模型中。

如何確定pdq的值？

1、引數p,q可以使用ACF和PACF圖發現。

2、如果相關係數ACF和偏相關係數PACF逐漸減小，這表明我們需要進行時間序列平穩並引入d引數。

選擇模型時，選擇AIC和BIC最小的(p,d,q)組合。

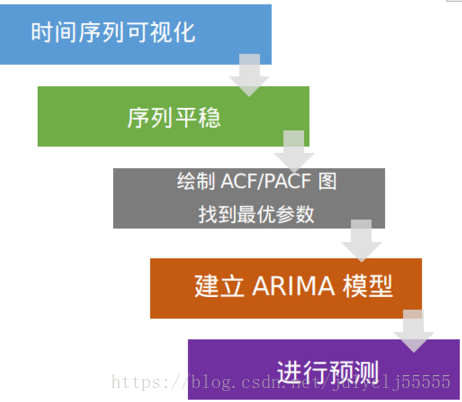
進行時間序列預測的步驟