使用Python為時間序列預測建立ARIMA模型
如何在Python中為時間序列預測建立ARIMA模型
ARIMA模型是一種流行且廣泛使用的時間序列預測統計方法。ARIMA是AutoRegressive Integrated Moving Average的縮寫。它是一類模型,它捕獲時間序列資料中的一套不同的標準時間結構。
ARIMA模型的資訊還可以參考這裡
在本教程中,您將瞭解如何使用Python為時間序列資料開發ARIMA模型。
完成本教程後,您將瞭解:
關於ARIMA模型使用的引數和模型所做的假設。
如何使ARIMA模型適合資料並使用它來進行預測。
如何根據時間序列問題配置ARIMA模型。
自迴歸整合移動平均模型
ARIMA模型是一類用於分析和預測時間序列資料的統計模型。它明確地迎合了時間序列資料中的一套標準結構,因此提供了一種簡單而強大的方法來進行熟練的時間序列預測。ARIMA是AutoRegressive Integrated Moving Average的縮寫。它是更簡單的AutoRegressive移動平均線的推廣,並添加了整合的概念。這個首字母縮略詞是描述性的,捕捉模型本身的關鍵方面。簡而言之,它們是:
AR:自迴歸。一種模型,它使用觀察與一些滯後觀察之間的依賴關係。
我:綜合。使用原始觀察的差分(例如,從前一時間步驟的觀察中減去觀察值)以使時間序列靜止。
MA:移動平均線。使用應用於滯後觀察的移動平均模型中的觀察和殘差之間的依賴關係的模型。
這些元件中的每一個都在模型中明確指定為引數。標準符號用於ARIMA(p,d,q),其中引數用整數值代替,以快速指示正在使用的特定ARIMA模型。
ARIMA模型的引數定義如下:
p:模型中包含的滯後觀察數,也稱為滯後順序。
d:原始觀測值的差異次數,也稱為差分程度。
q:移動平均視窗的大小,也稱為移動平均值的順序。
構建包括指定數量和型別的項的線性迴歸模型,並且通過差分程度準備資料以使其靜止,即去除對迴歸模型產生負面影響的趨勢和季節結構。
值0可用於引數,表示不使用模型的該元素。這樣,ARIMA模型可以配置為執行ARMA模型的功能,甚至是簡單的AR,I或MA模型。對時間序列採用ARIMA模型假設生成觀察的基礎過程是ARIMA過程。這似乎是顯而易見的,但有助於激發在原始觀測中確認模型假設的必要性以及模型預測的殘差。接下來,我們來看看如何在Python中使用ARIMA模型。我們將從載入一個簡單的單變數時間序列開始。
洗髮水銷售資料集
該資料集描述了3年期間每月洗髮水的銷售數量。單位是銷售計數,有36個觀察。 原始資料集歸功於Makridakis,Wheelwright和Hyndman(1998)。瞭解有關資料集的更多資訊並從此處下載。下載資料集並將其放在當前工作目錄中,檔名為“shampoo-sales.csv”。下面是使用Pandas載入Shampoo Sales資料集以及解析日期時間欄位的自定義函式的示例。 資料集以任意年份為基線,在本例中為1900。
from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot
def parser(x):
return datetime.strptime('190'+x, '%Y-%m')
series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
print(series.head())
series.plot()
pyplot.show()輸出前五行資料如下:
Month
1901-01-01 266.0
1901-02-01 145.9
1901-03-01 183.1
1901-04-01 119.3
1901-05-01 180.3
Name: Sales, dtype: float64資料也繪製為時間序列,沿x軸的月份和y軸的銷售數字。

我們可以看到Shampoo Sales資料集有一個明顯的趨勢。這表明時間序列不是靜止的並且需要差分以使其靜止,至少差異為1。讓我們快速瀏覽一下時間序列的自相關圖。 這也是Pandas內建的。 下面的示例繪製了時間序列中大量滯後的自相關。
from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot
from pandas.tools.plotting import autocorrelation_plot
def parser(x):
return datetime.strptime('190'+x, '%Y-%m')
series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
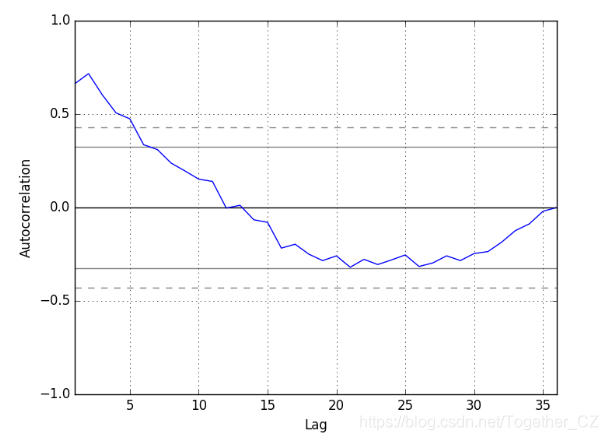
autocorrelation_plot(series)
pyplot.show()執行這個例子,我們可以看到與前10個到12個滯後的正相關,這可能對前5個滯後很重要。模型的AR引數的良好起點可以是5。
ARIMA與Python
statsmodels庫提供適合ARIMA模型的功能。可以使用statsmodels庫建立ARIMA模型,如下所示:通過呼叫ARIMA()並傳入p,d和q引數來定義模型。通過呼叫fit()函式在訓練資料上準備模型。可以通過呼叫predict()函式並指定要預測的時間或索引的時間索引來進行預測。讓我們從簡單的事情開始吧。 我們將ARIMA模型與整個Shampoo Sales資料集相匹配,並檢查殘差。首先,我們適合ARIMA(5,1,0)模型。 這將自動迴歸的滯後值設定為5,使用差值順序1使時間序列靜止,並使用0的移動平均模型。在擬合模型時,提供了大量關於線性迴歸模型擬合的除錯資訊。 我們可以通過將disp引數設定為0來關閉它。
from pandas import read_csv
from pandas import datetime
from pandas import DataFrame
from statsmodels.tsa.arima_model import ARIMA
from matplotlib import pyplot
def parser(x):
return datetime.strptime('190'+x, '%Y-%m')
series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
# fit model
model = ARIMA(series, order=(5,1,0))
model_fit = model.fit(disp=0)
print(model_fit.summary())
# plot residual errors
residuals = DataFrame(model_fit.resid)
residuals.plot()
pyplot.show()
residuals.plot(kind='kde')
pyplot.show()
print(residuals.describe())執行該示例將列印擬合模型的摘要。 這總結了所使用的係數值以及樣本內觀察的擬合技巧。
ARIMA Model Results
==============================================================================
Dep. Variable: D.Sales No. Observations: 35
Model: ARIMA(5, 1, 0) Log Likelihood -196.170
Method: css-mle S.D. of innovations 64.241
Date: Mon, 12 Dec 2016 AIC 406.340
Time: 11:09:13 BIC 417.227
Sample: 02-01-1901 HQIC 410.098
- 12-01-1903
=================================================================================
coef std err z P>|z| [95.0% Conf. Int.]
---------------------------------------------------------------------------------
const 12.0649 3.652 3.304 0.003 4.908 19.222
ar.L1.D.Sales -1.1082 0.183 -6.063 0.000 -1.466 -0.750
ar.L2.D.Sales -0.6203 0.282 -2.203 0.036 -1.172 -0.068
ar.L3.D.Sales -0.3606 0.295 -1.222 0.231 -0.939 0.218
ar.L4.D.Sales -0.1252 0.280 -0.447 0.658 -0.674 0.424
ar.L5.D.Sales 0.1289 0.191 0.673 0.506 -0.246 0.504
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 -1.0617 -0.5064j 1.1763 -0.4292
AR.2 -1.0617 +0.5064j 1.1763 0.4292
AR.3 0.0816 -1.3804j 1.3828 -0.2406
AR.4 0.0816 +1.3804j 1.3828 0.2406
AR.5 2.9315 -0.0000j 2.9315 -0.0000
-----------------------------------------------------------------------------首先,我們得到殘差的線圖,表明模型可能仍然存在一些趨勢資訊。

接下來,我們得到殘差誤差值的密度圖,表明誤差是高斯誤差,但可能不是以零為中心。

顯示殘差的分佈。 結果表明,預測中確實存在偏差(殘差中的非零均值)。
count 35.000000
mean -5.495213
std 68.132882
min -133.296597
25% -42.477935
50% -7.186584
75% 24.748357
max 133.237980請注意,雖然上面我們使用整個資料集進行時間序列分析,但理想情況下,我們會在開發預測模型時僅對訓練資料集執行此分析。接下來,讓我們看看如何使用ARIMA模型進行預測。
滾動預測ARIMA模型
ARIMA模型可用於預測未來的時間步長。我們可以使用ARIMAResults物件上的predict()函式進行預測。它接受將預測作為引數的時間步長索引。這些索引與用於進行預測的訓練資料集的起點相關。如果我們在訓練資料集中使用100個觀測值來擬合模型,那麼用於進行預測的下一個時間步驟的索引將被指定給預測函式,如start = 101,end = 101。這將返回一個包含預測的一個元素的陣列。如果我們執行任何差分(在配置模型時d> 0),我們也希望預測值在原始比例中。這可以通過將typ引數設定為'levels'值來指定:typ ='levels'。或者,我們可以通過使用forecast()函式來避免所有這些規範,該函式使用模型執行一步預測。我們可以將訓練資料集拆分為訓練集和測試集,使用訓練集來擬合模型,併為測試集上的每個元素生成預測。考慮到差異的先前時間步長和AR模型的觀察依賴性,需要滾動預測。執行此滾動預測的一種粗略方法是在收到每個新觀察後重新建立ARIMA模型。我們手動跟蹤名為歷史的列表中的所有觀察結果,該列表與訓練資料一起播種,並且每次迭代都附加新的觀察結果。綜上所述,下面是使用Python中的ARIMA模型進行滾動預測的示例。
from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot
from statsmodels.tsa.arima_model import ARIMA
from sklearn.metrics import mean_squared_error
def parser(x):
return datetime.strptime('190'+x, '%Y-%m')
series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
X = series.values
size = int(len(X) * 0.66)
train, test = X[0:size], X[size:len(X)]
history = [x for x in train]
predictions = list()
for t in range(len(test)):
model = ARIMA(history, order=(5,1,0))
model_fit = model.fit(disp=0)
output = model_fit.forecast()
yhat = output[0]
predictions.append(yhat)
obs = test[t]
history.append(obs)
print('predicted=%f, expected=%f' % (yhat, obs))
error = mean_squared_error(test, predictions)
print('Test MSE: %.3f' % error)
# plot
pyplot.plot(test)
pyplot.plot(predictions, color='red')
pyplot.show()執行該示例會在每次迭代時列印預測值和期望值。我們還可以計算預測的最終均方誤差分數(MSE),為其他ARIMA配置提供比較點。
predicted=349.117688, expected=342.300000
predicted=306.512968, expected=339.700000
predicted=387.376422, expected=440.400000
predicted=348.154111, expected=315.900000
predicted=386.308808, expected=439.300000
predicted=356.081996, expected=401.300000
predicted=446.379501, expected=437.400000
predicted=394.737286, expected=575.500000
predicted=434.915566, expected=407.600000
predicted=507.923407, expected=682.000000
predicted=435.483082, expected=475.300000
predicted=652.743772, expected=581.300000
predicted=546.343485, expected=646.900000
Test MSE: 6958.325建立一個線圖,顯示與滾動預測預測(紅色)相比的預期值(藍色)。 我們可以看到這些值顯示出一些趨勢,並且具有正確的比例。
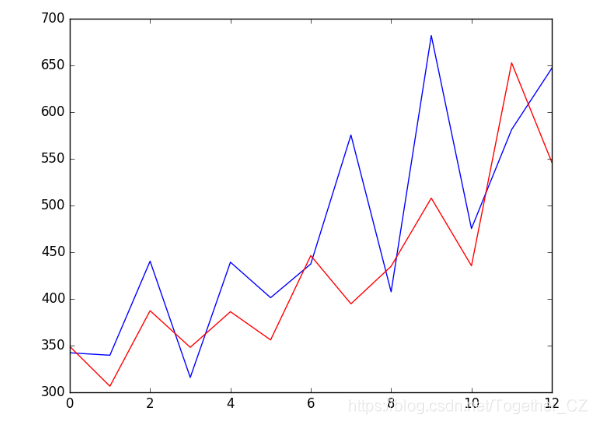
該模型可以使用p,d甚至q引數的進一步調整。
配置ARIMA模型
擬合ARIMA模型的經典方法是遵循Box-Jenkins方法。這是一個使用時間序列分析和診斷來發現ARIMA模型的良好引數的過程。總之,該過程的步驟如下:
模型識別。使用圖和彙總統計資料來識別趨勢,季節性和自迴歸元素,以瞭解差異量和所需滯後的大小。
引數估計。使用擬合程式查找回歸模型的係數。
模型檢查。使用殘差的圖和統計檢驗來確定模型未捕獲的時間結構的數量和型別。重複該過程,直到在樣品內或樣品外觀察(例如訓練或測試資料集)上達到所需的擬合水平。
這個過程在經典的1970年教科書中描述,主題為時間序列分析:George Box和Gwilym Jenkins的預測和控制。如果您有興趣深入瞭解這種型別的模型和方法,現在可以獲得更新的第5版。鑑於該模型可以有效地適應中等大小的時間序列資料集,模型的網格搜尋引數可能是一種有價值的方法。
