影象處理基礎(7):影象的灰度變換
前面幾篇文章介紹的是影象的空間域濾波,其對畫素的處理都是基於畫素的某一鄰域進行的。本文介紹的影象的灰度變換則不同,其對畫素的計算僅僅依賴於當前畫素和灰度變換函式。
灰度變換也被稱為影象的點運算(只針對影象的某一畫素點)是所有影象處理技術中最簡單的技術,其變換形式如下:
s = T(r)
其中,T是灰度變換函式;r是變換前的灰度;s是變換後的畫素。
影象灰度變換的有以下作用:
- 改善影象的質量,使影象能夠顯示更多的細節,提高影象的對比度(對比度拉伸)
- 有選擇的突出影象感興趣的特徵或者抑制影象中不需要的特徵
- 可以有效的改變影象的直方圖分佈,使畫素的分佈更為均勻
常見的灰度變換
灰度變換函式描述了輸入灰度值和輸出灰度值之間變換關係,一旦灰度變換函式確定下來了,那麼其輸出的灰度值也就確定了。可見灰度變換函式的性質就決定了灰度變換所能達到的效果。用於影象灰度變換的函式主要有以下三種:
- 線性函式 (影象反轉)
- 對數函式:對數和反對數變換
- 冪律函式:n次冪和n次開方變換
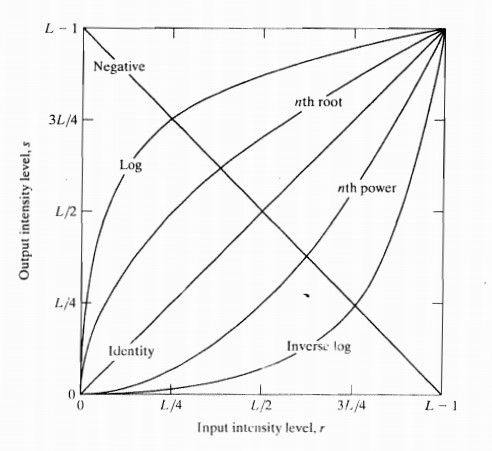
上圖給出了幾種常見灰度變換函式的曲線圖,根據這幾種常見函式的曲線形狀,可以知道這幾種變換的所能達到的效果。例如,對數變換和冪律變換都能實現影象灰度級的擴充套件/壓縮,另外對數變換還有一個重要的性質,它能壓縮影象灰度值變換較大的影象的動態範圍(例如,傅立葉變換的頻譜顯示)。
線性變換
令r為變換前的灰度,s為變換後的灰度,則線性變換的函式:
其中,a為直線的斜率,b為在y軸的截距。選擇不同的a,b值會有不同的效果:
- a>1” role=”presentation” style=”position: relative;”>a>1a>1,增加影象的對比度
- a<1” role=”presentation” style=”position: relative;”>a<1a<1,減小影象的對比度
- a=1且b≠0” role=”presentation” style=”position: relative;”>a=1且b≠0a=1且b≠0,影象整體的灰度值上移或者下移,也就是影象整體變亮或者變暗,不會改變影象的對比度。
- a<0且b=0” role=”presentation” style=”position: relative;”>a<0且b=0a<0且b=0,影象的亮區域變暗,暗區域變亮
- a=1且b=0” role=”presentation” style=”position: relative;”>a=1且b=0a=1且b=0,恆定變換,不變
- a=−1且b=255” role=”presentation” style=”position: relative;”>a=−1且b=255a=−1且b=255,影象反轉。
在進行影象增強時,上述的線性變換函式用的較多的就是影象反轉了,根據上面的引數,影象反轉的變換函式為:s=255−s” role=”presentation” style=”position: relative;”>s=255−ss=255−s。影象反轉得到的是影象的負片,能夠有效的增強在影象暗區域的白色或者灰色細節。其效果如下:

影象反轉的實現是比較簡單的,在OpenCV中有對Mat的運算子過載,可以直接Mat r = 255 - img或者~img來實現。
對數變換
對數變換的通用公式是:
其中,c是一個常數,,假設 r≥0” role=”presentation” style=”position: relative;”>r≥0r≥0,根據上圖中的對數函式的曲線可以看出:對數變換,將源影象中 範圍較窄的低灰度值對映到範圍較寬的灰度區間,同時將範圍較寬的高灰度值區間對映為較窄的灰度區間,從而擴充套件了暗畫素的值,壓縮了高灰度的值,能夠對影象中低灰度細節進行增強。;從函式曲線也可以看出,反對數函式的曲線和對數的曲線是對稱的,在應用到影象變換其結果是相反的,反對數變換的作用是壓縮灰度值較低的區間,擴充套件高灰度值的區間。
基於OpenCV的實現,其對數變換的程式碼如下:
float pixels[256];
for (int i = 0; i < 256; i++)
pixels[i] = log(1 + i);
Mat imageLog(image.size(), CV_32FC3);
for (int i = 0; i<image.rows; i++)
{
for (int j = 0; j<image.cols; j++)
{
imageLog.at<Vec3f>(i, j)[0] = pixels[image.at<Vec3b>(i, j)[0]];
imageLog.at<Vec3f>(i, j)[1] = pixels[image.at<Vec3b>(i, j)[1]];
imageLog.at<Vec3f>(i, j)[2] = pixels[image.at<Vec3b>(i, j)[2]];
}
}
//歸一化到0~255
normalize(imageLog, imageLog, 0, 255, CV_MINMAX);
//轉換成8bit影象顯示
convertScaleAbs(imageLog, imageLog);這使用的對數函式的底為10。由於灰度變換是灰度值之間的一對一的對映,而灰度值區間通常為[0,255],所以在進行灰度變換時,通常使用查表法。也就是,現將每個灰度值的對映後的結果計算出來,在變換時,通過查表得到變換後的灰度值。執行上面結果得到的結果如下:
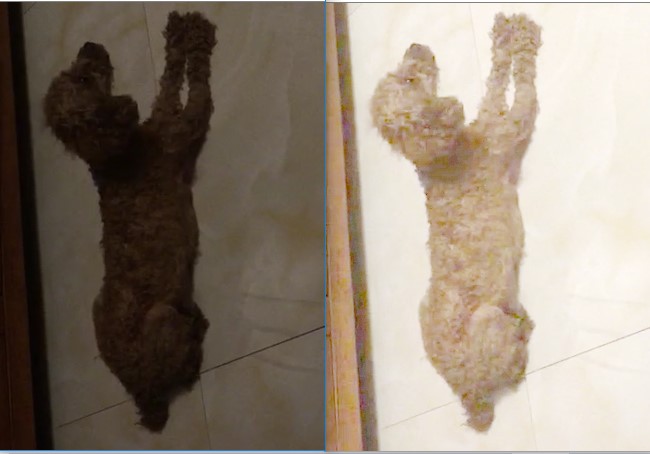
左邊為原影象,其拍攝環境較暗,無法分辨出很多的細節;右邊為變換後的影象,整個影象明亮許多,也能分辨出原圖中處於暗區域的狗狗的更多細節。
對數變換,還有一個很重要的性質,能夠壓縮影象畫素的動態範圍。例如,在進行傅立葉變換時,得到的頻譜的動態範圍較大,頻譜值的範圍通常為[0,106]” role=”presentation” style=”position: relative;”>[0,106][0,106],甚至更高。這樣範圍的值,顯示器是無法完整的顯示如此大範圍的灰度值的,因而許多灰度細節會被丟失掉。而將得到的頻譜值進行對數變換,可以將其動態範圍變換到一個合適區間,這樣就能夠顯示更多的細節。
冪律變換(伽馬變換)
伽馬變換的公式為:
其中c和 γ” role=”presentation” style=”position: relative;”>γγ為正常數。
伽馬變換的效果與對數變換有點類似,當 γ>1” role=”presentation” style=”position: relative;”>γ>1γ>1時,情況相反,與反對數變換類似。其函式曲線如下:
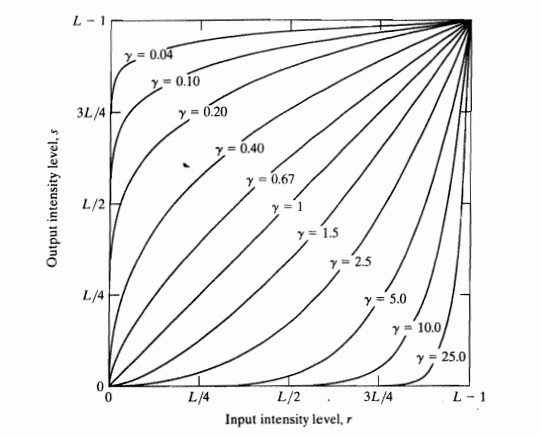
當γ<1” role=”presentation” style=”position: relative;”>γ<1γ<1的值越大,對影象高灰度值部分的擴充套件越明顯。這樣就能夠顯示更多的影象的低灰度或者高灰度細節。
伽馬變換主要用於影象的校正,對灰度值過高(影象過亮)或者過低(影象過暗)的影象進行修正,增加影象的對比度,從而改善影象的顯示效果。
基於OpenCV的實現:
float pixels[256];
for (int i = 0; i < 256; i++)
pixels[i] = i * i *i;
Mat imageLog(image.size(), CV_32FC3);
for (int i = 0; i<image.rows; i++)
{
for (int j = 0; j<image.cols; j++)
{
imageLog.at<Vec3f>(i, j)[0] = pixels[image.at<Vec3b>(i, j)[0]];
imageLog.at<Vec3f>(i, j)[1] = pixels[image.at<Vec3b>(i, j)[1]];
imageLog.at<Vec3f>(i, j)[2] = pixels[image.at<Vec3b>(i, j)[2]];
}
}
//歸一化到0~255
normalize(imageLog, imageLog, 0, 255, CV_MINMAX);
//轉換成8bit影象顯示
convertScaleAbs(imageLog, imageLog);這裡選擇的引數為c = 1,γ=3” role=”presentation” style=”position: relative;”>γ=3γ=3,來擴充套件影象的高灰度區域,其結果如下:

當選擇引數為c = 1,γ=0.4” role=”presentation” style=”position: relative;”>γ=0.4γ=0.4,來擴充套件影象的低灰度區域,其效果如下:

根據以上的結果,結合伽馬變換的函式曲線圖,做如下總結:
- γ>1” role=”presentation” style=”position: relative;”>γ>1γ>1區間。這樣變換的結果就是,低於K的灰度區域被壓縮到更低灰度區間,而較亮的高灰度區域的灰度值被擴充套件到較大的灰度區間變的不那麼亮,整體的效果就是影象的對比度增加了,但是由於亮度區域被擴充套件,也就不那麼亮了。
- γ<1” role=”presentation” style=”position: relative;”>γ<1γ<1時,會將灰度值較小的低灰度區域擴充套件到較寬的灰度區間,而將較寬的高灰度區域壓縮到較小的灰度區間。這樣變換的效果就是,低灰度區域擴充套件開來,變亮;而寬的高灰度區域,被壓縮的較窄的區間,也變亮了,故變換後的整體效果是變亮了。
基於OpenCV的灰度變換實現
灰度變換屬於點對點的一一變換,在實現的時候,可以利用查表法。也就是實現將[0,255]區間的各個灰度值的變換後的值計算出來,在變換的時候直接根據灰度值進行查表得到變換後的結果。其實現如下:
/////////////////////////////////////////////////////////////////////
//
// 灰度線性變換函式
// 引數:
// src,輸入原影象
// dst,輸出影象,型別為CV_32F,大小及通道數與原影象相同
// mapping,灰度對映表,可以根據不同的變換函式,提前計算好影象的灰度對映表
//
////////////////////////////////////////////////////////////////////
void gray_trans(const Mat& src, Mat& dst,float* mapping)
{
int channels = src.channels();
if (channels == 1)
{
dst = Mat(src.size(), CV_32FC1);
for (int i = 0; i < src.rows; i++)
{
float* p1 = dst.ptr<float>(i);
const uchar* p2 = src.ptr<uchar>(i);
for (int j = 0; j < src.cols; j++)
p1[j] = mapping[p2[j]];
}
}
else if (channels == 3)
{
dst = Mat(src.size(), CV_32FC3);
for (int i = 0; i < src.rows; i++)
{
float* p1 = dst.ptr<float>(i);
const uchar* p2 = src.ptr<uchar>(i);
for (int j = 0; j < src.cols * 3; j+=3)
{
p1[j] = mapping[p2[j]];
p1[j+1] = mapping[p2[j+1]];
p1[j+2] = mapping[p2[j+2]];
}
}
}
}其呼叫也比較簡單,根據具體的灰度變換函式,填充灰度對映表即可,以伽馬變換為例:
float pixels[256];
for (int i = 0; i < 256; i++)
pixels[i] = powf(i, 1.5);
Mat imageLog;
gray_trans(image, imageLog, pixels);總結
本文主要對影象的幾種常見的灰度變換進行了總結。
- 影象反轉,是影象線性變換的一種,可以得到影象負片,能夠有效的增強影象的暗色區域中的白色或者灰色細節
- 對數變換,擴充套件影象中的低灰度區域,壓縮影象中的高灰度區域,能夠增強影象中的暗色區域的細節;反對數變換與此相反。對數變換還有個重要作用是,能夠壓縮影象灰度值的動態範圍,在傅立葉變換中能夠顯示更多的變換後的頻譜細節。
- 伽馬變換,主要用於影象的校正,根據引數γ的選擇不同,能夠修正影象中灰度過高(γ>1)或者灰度過低(y<1) 。
