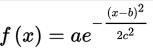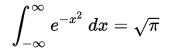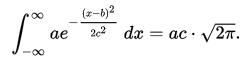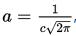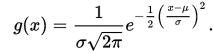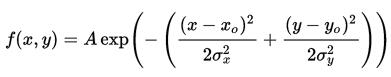高斯函式(Gaussian function)的詳細分析
摘要
論文中遇到很重要的一個元素就是高斯核函式,但是必須要分析出高斯函式的各種潛在屬性,本文首先參考相關材料給出高斯核函式的基礎,然後使用matlab自動儲存不同引數下的高斯核函式的變化gif動圖,同時分享出原始碼,這樣也便於後續的論文寫作。
高斯函式的基礎
2.1 一維高斯函式
高斯函式,Gaussian Function, 也簡稱為Gaussian,一維形式如下:
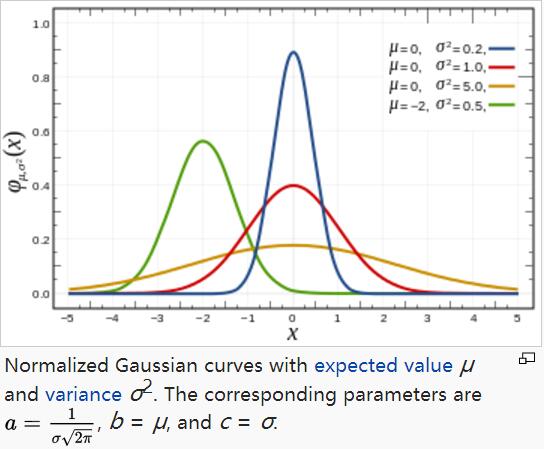
對於任意的實數a,b,c,是以著名數學家Carl Friedrich Gauss的名字命名的。高斯的一維圖是特徵對稱“bell curve”形狀,a是曲線尖峰的高度,b是尖峰中心的座標,c稱為標準方差,表徵的是bell鍾狀的寬度。
高斯函式廣泛應用於統計學領域,用於表述正態分佈,在訊號處理領域,用於定義高斯濾波器,在影象處理領域,二維高斯核函式常用於高斯模糊Gaussian Blur,在數學領域,主要是用於解決熱力方程和擴散方程,以及定義Weiertrass Transform。
從上圖可以看出,高斯函式是一個指數函式,其log函式是對數凹二次函式 whose logarithm a concave quadratic function。
高斯函式的積分是誤差函式error function,儘管如此,其在整個實線上的反常積分能夠被精確的計算出來,使用如下的高斯積分
同理可得
當且僅當
上式積分為1,在這種情況下,高斯是正態分佈隨機變數的概率密度函式,期望值μ=b,方差delta^2 = c^2,即
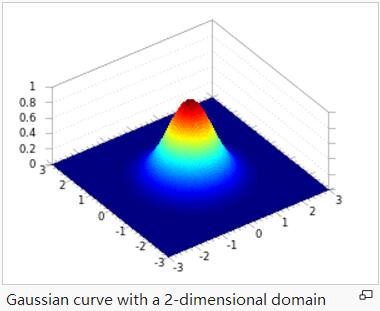
2.2 二維高斯函式
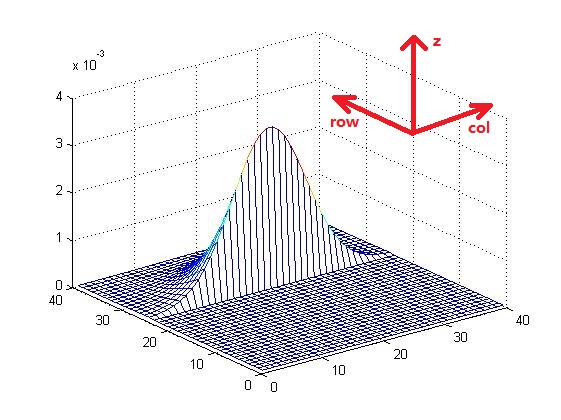
二維高斯函式,形如
A是幅值,x。y。是中心點座標,σx σy是方差,圖示如下,A = 1, xo = 0, yo = 0, σx = σy = 1
2.3 高斯函式分析
這一節使用matlab直觀的檢視高斯函式,在實際程式設計應用中,高斯函式中的引數有
ksize 高斯函式的大小
sigma 高斯函式的方差
center 高斯函式尖峰中心點座標
bias 高斯函式尖峰中心點的偏移量,用於控制截斷高斯函式
為了方便直觀的觀察高斯函式引數改變而結果也不一樣,下面的程式碼實現了引數的自動遞增,並且將所有的結果圖儲存為gif影象,首先貼出完整程式碼:
function mainfunc()
% 測試高斯函式,遞增的方法實現高斯函式引數的改變對整個高斯函式的影響,
% 並自動儲存為gif格式輸出。
% created by zhao.buaa 2016.09.28
%% 儲存gif動畫
item = 10; % 迭代次數
dt = 1; % 步長大小
ksize =20; % 高斯大小
sigma = 2; % 方差大小
% filename = ['ksize-' num2str(ksize) '--' num2str(ksize+dt*item) '-sigma-' num2str(sigma) '.gif']; %必須預先建立gif檔案
filename = ['ksize-' num2str(ksize) '-sigma-' num2str(sigma) '--' num2str(sigma+dt*item) '.gif']; %必須預先建立gif檔案
% main loop
for i = 1:item
center = round(ksize/2); % 中心點
bias = ksize*10/10; % 偏移中心點量
ksigma = ksigma(ksize, sigma, center, bias); % 構建核函式
tname = ['ksize-' num2str(ksize) '-sigma-' num2str(sigma) '-center-' num2str(center)];
figure(i), mesh(ksigma), title(tname);
%設定固定的x-y-z座標範圍,便於觀察,axis([xmin xmax ymin ymax zmin zmax])
axis([0 ksize 0 ksize 0 0.008]); view([0, 90]);% 改變可視角度
% ksize 遞增
% ksize = ksize + 10;
% sigma 遞增
sigma = sigma + dt;
% 自動儲存為gif影象
frame = getframe(i);
im = frame2im(frame);
[I,map] = rgb2ind(im,256);
if i==1
imwrite(I,map,filename,'gif','Loopcount',inf, 'DelayTime',0.4);
else
imwrite(I,map,filename,'gif','WriteMode','append','DelayTime',0.4);
end
end;
close all;
%% 截斷高斯核函式,截斷的程度取決於引數bias
function ksigma = ksigma(ksize, sigma, center,bias)
%ksize = 80; sigma = 15;
ksigma=fspecial('gaussian',ksize, sigma); % 構建高斯函式
[m, n] =size(ksigma);
for i = 1:m
for j = 1:n
if( (i<center-bias)||(i>center+bias)||(j<center-bias)||(j>center+bias) )
ksigma(i,j) = 0;
end;
end;
end;
結果圖:
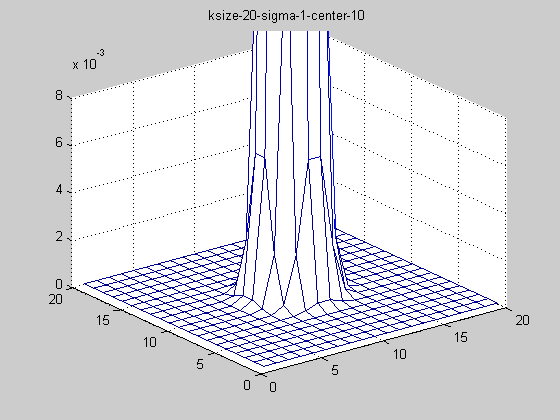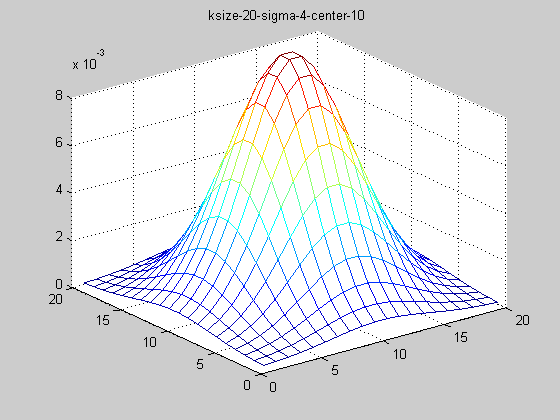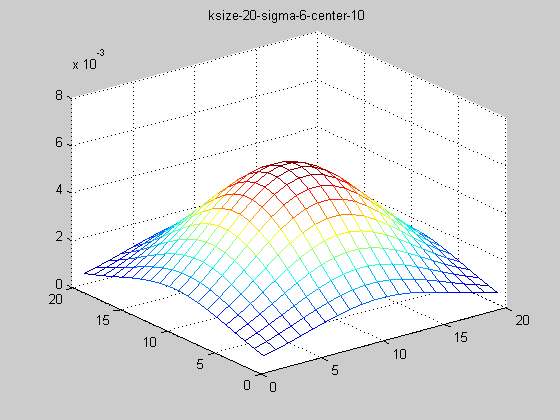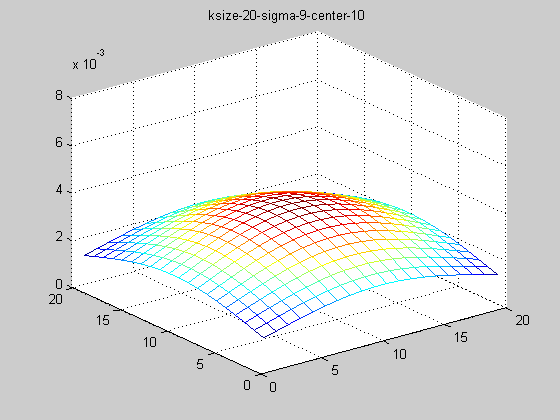
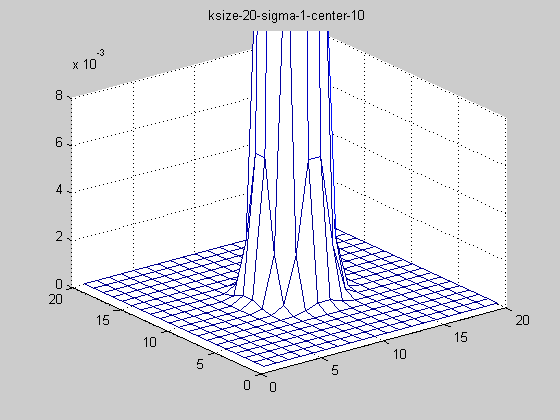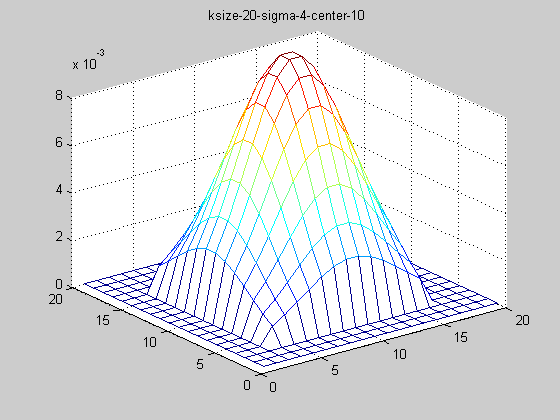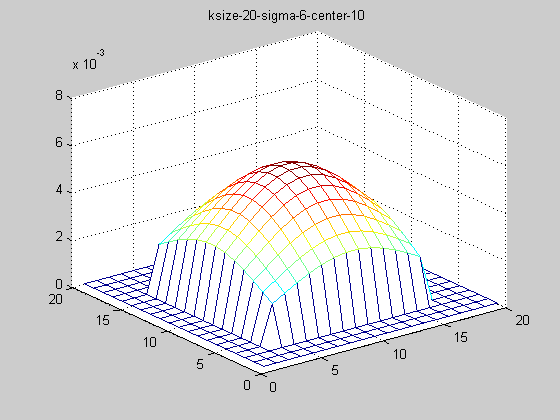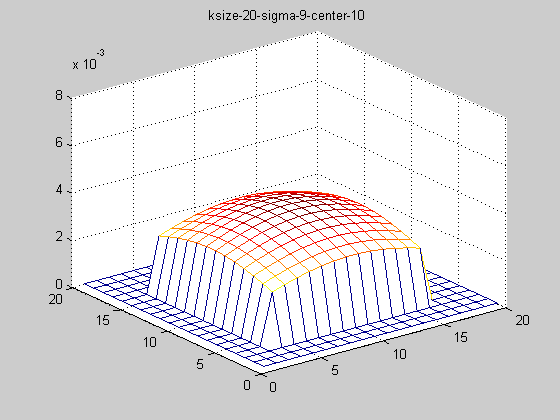
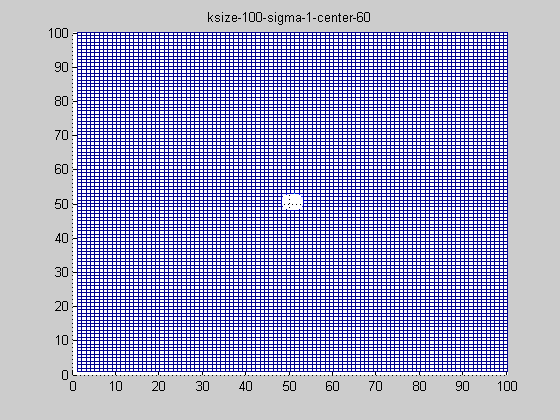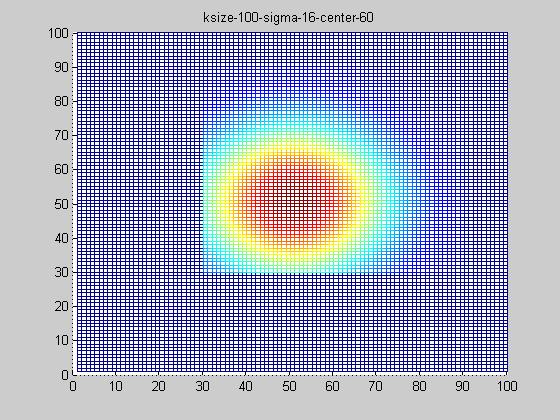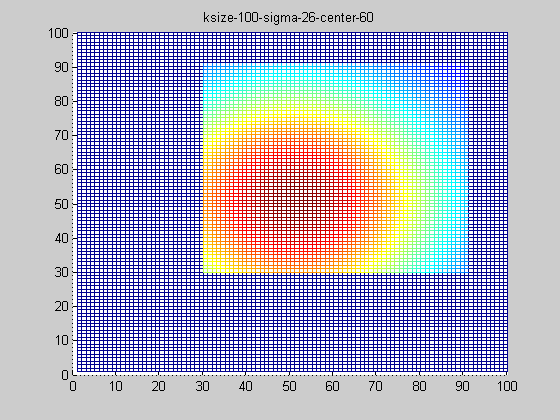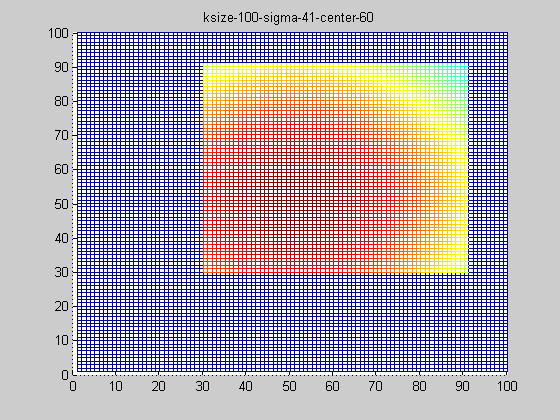
固定ksize為20,sigma從1-9,固定center在高斯中間,並且bias偏移量為整個半徑,即原始高斯函式。
隨著sigma的增大,整個高斯函式的尖峰逐漸減小,整體也變的更加平緩,則對影象的平滑效果越來越明顯。
保持引數不變,對上述高斯函式進行截斷,即truncated gaussian function,bias的大小為ksize*3/10,則結果如下圖:
truncated gaussian function的作用主要是對超過一定區域的原始影象資訊不再考慮,這就保證在更加合理的利用靠近高斯函式中心點的周圍畫素,同時還可以改變高斯函式的中心座標,如下圖:
為了便於觀察截斷的效果,改變了可視角度。
高斯核函式卷積
論文中使用gaussian與feature map做卷積,目前的結果來看,要做到隨著到邊界的距離改變高斯函式的截斷引數,因為影象的邊緣如果使用原始高斯函式,就會在邊界地方出現特別低的一圈,原因也很簡單,高斯函式在與原始影象進行高斯卷積的時候,影象邊緣外為0計算的,那麼如何解決邊緣問題呢?
先看一段程式碼:
[plain] view plain copy
- % 截斷高斯核函式
- ksize = 40; ksigma=fspecial('gaussian', ksize, 6);
- [m, n] =size(ksigma);
- for i = 1:m
- for j = 1:n
- if( i<25 )
- ksigma(i,j) = 0;
- end;
- end;
- end;
- figure, mesh(ksigma);
在i,即row上對高斯核函式進行截斷,bias為半徑大小,則如圖6
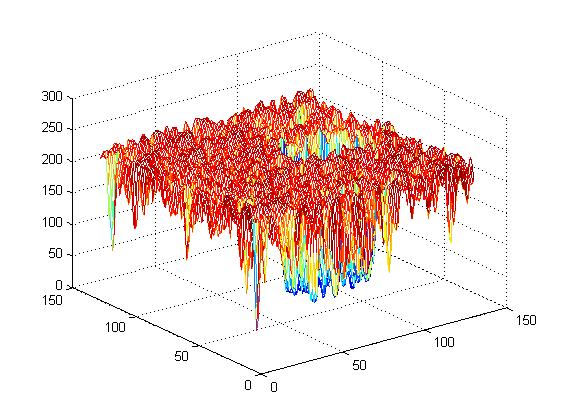
並且對下圖7進行卷積,
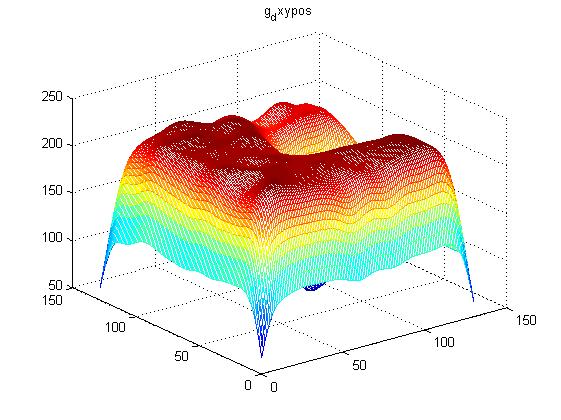
首先卷積核為原始未截斷高斯核函式,則結果如圖8
可以看出,在影象邊緣處的卷積結果出現不想預見的結果,邊緣處的值出現大幅度減少的情況,這是高斯核函式在邊緣處將影象外的部分當成0計算的結果,因此,需要對高斯核函式進行鍼對性的截斷處理,但是前提是要掌握bias的規律,下面就詳細分析。
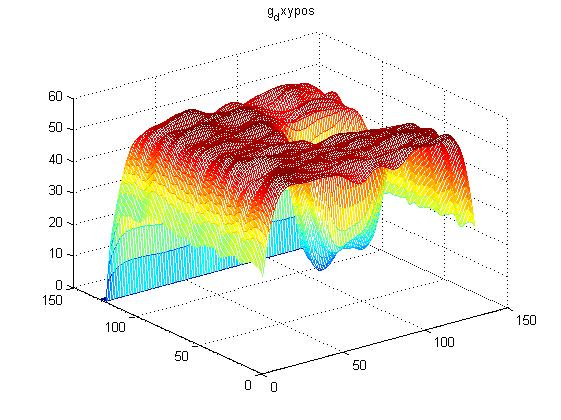
如果使用圖6的高斯核函式與圖7做卷積操作,則如圖9:
可以看出,相比較於圖8,與高斯核函式相對應的部分出現了變化,也就是說:
[plain] view plain copy
- if( i<25 )
- ksigma(i,j) = 0;
- end;
靠近邊緣的時候,改變 i 或 j 的值,即可保證邊緣處的平滑處理。但是這樣改變高斯核函式,使用matlab不是很好解決這個問題,還是使用將待處理影象邊緣向外部擴充套件bias的大小,與標準高斯核函式做卷積,再將超過原始影象大小的部分剪下掉,目前來看在使用matlab中imfilter函式做卷積運算最合適且最簡單的處理方法了,先寫在這裡,此部分並不是論文中的核心部分,只是數值運算的技巧性程式設計方法。
設計影象處理
深入地探討高斯濾波與影象處理的關聯,包括引數的影響、引數的選取、高斯模板的形成以及自行程式設計實現高斯濾波的效果與openCV函式實現效果比對。
說道“sigma表示的是標準差,如果標準差比較小,這是就相當於影象點運算,則平滑效果不明顯;反之,標準差比較大,則相當於平均模板,比較模糊”,那麼這麼說可能很多人包括一開始的我並不是很理解,這是為什麼呢,那麼我們需要從高斯函式談起:

這樣一個高斯函式的概率分佈密度如下圖所示:

我們要理解好這個圖,橫軸表示可能得取值x,豎軸表示概率分佈密度F(x),那麼不難理解這樣一個曲線與x軸圍成的圖形面積為1。sigma(標準差)決定了這個圖形的寬度,我給出下述結論:sigma越大,則圖形越寬,尖峰越小,圖形較為平緩;sigma越小,則圖形越窄,越集中,中間部分也就越尖,圖形變化比較劇烈。這其實很好理解,如果sigma也就是標準差越大,則表示該密度分佈一定比較分散,由於面積為1,於是尖峰部分減小,寬度越寬(分佈越分散);同理,當sigma越小時,說明密度分佈較為集中,於是尖峰越尖,寬度越窄!
理解好上述結論之後,那麼(一)中的結論當然也就順理成章了,sigma越大,分佈越分散,各部分比重差別不大,於是生成的模板各元素值差別不大,類似於平均模板;sigma越小,分佈越集中,中間部分所佔比重遠遠高於其他部分,反映到高斯模板上就是中心元素值遠遠大於其他元素值,於是自然而然就相當於中間值得點運算。
程式也可以驗證如下:
視窗尺寸:3*3 sigma = 0.1
視窗尺寸:3*3 sigma = 0.8
視窗尺寸:3*3 sigma = 2
接著,我們來重點討論下高斯模板,在初學高斯濾波的時候,用得最多的也是最經典的一個3*3模板就是
[1 2 1 ]
[ 2 4 2 ]
[1 2 1]
,當時我就很納悶這個模板是怎麼出來的,後來我經過多方查詢資料,基本得到了如下的解釋:高斯模板實際上也就是模擬高斯函式的特徵,具有對稱性並且數值由中心向四周不斷減小,這個模板剛好符合這樣的特性,並且非常簡單,容易被大家接受,於是就比較經典!但是這樣一個簡單的矩陣是遠遠不能滿足我們對影象處理的要求的,我們需要按照自己的要求得到更加精確的模板,那麼接下來我們就程式設計實現自己想要的高斯模板。部分關鍵函式如下:
double** createG(int iSize, double sigma)
{
double **guass;
double sum = 0;
double x2 = 0;
double y2 = 0;
int center = (iSize - 1) / 2;
guass = new double*[iSize];//注意,double*[k]表示一個有10個元素的指標陣列
for (int i = 0; i < iSize; ++i)
{
guass[i] = new double[iSize];
}
for (int i = 0; i<iSize; i++)
{//使用x2,y2降低了運算速度,提高了程式的效率
x2 = pow(double(i - center), 2);
for (int j = 0; j<iSize; j++)
{
y2 = pow(double(j - center), 2);
sum += guass[i][j] = exp(-(x2 + y2) / (2 * sigma*sigma));
}
}
if (sum != 0)
{
//歸一化
for (int i = 0; i<iSize; i++)
{
for (int j = 0; j<iSize; j++)
{
guass[i][j] /= sum;
}
}
}
return guass;
}
上述的這個函式就是返回的一個使用者想要的高斯模板,其輸入引數iSize表示模板大小(這裡先只考慮方陣模板),輸入引數sigma表示高斯函式標準差,聰明的你應該一眼就看出這個程式實際上就是按照公式根據規定的矩陣大小進行離散化得到相應的資料。縱觀整個程式,我覺得最不好理解的是那個引數center,這是個什麼引數呢?通過程式可以看出為什麼center與iSize呈2center+1的關係呢?而且,為什麼x2,y2是那樣取值呢?這實際上是模擬的一種距離關係。舉個例子來說:
假設我現在想要使用視窗尺寸為2k+1*2k+1的高斯模板對點進行操作,那麼假設這個高斯模板的第一個元素地址記為為(1,1),那麼高斯模板中心元素很容易算出為(k,k)。假設現在在計算模板中(i,j)元素值,那麼公式中的x2模擬為該點到中心點的距離,即i-k-1(為什麼要-1,讀者不妨自己自己寫個3*3的矩陣,看看(1,1)元素到(2,2)元素是不是要走兩步)。但是程式中是沒有-1的,這是因為程式中的i是從0開始的!於是這個center引數實際上就是代表的中心點!
執行結果:
我的程式執行的結果:3*3,sigma=1
Matlab的程式執行的結果:3*3,sigma=1
可以看出,相差無幾,這個程式是成功的!
然後,最重要的部分當然是使用上述高斯模板對影象進行濾波處理得到想要的效果,那麼接下來重點論述濾波處理。要理解好高斯濾波,自己寫高斯濾波的演算法當然是最好的,然後再和openCV的函式進行效果比對,這樣,算是對高斯濾波有了比較好的認識和理解了!
在很多資料上,我們都看到高斯函式的這樣一個特性,可分離性,意思是一個二維的高斯函式可以分解成相同的一維高斯函式處理兩遍,得到的效果是一樣的,但是處理時間卻大大縮短了。
我們可以想到,二維函式直接處理會是這樣的:
for(int i = 0; i < img->height; ++i)
for(int j = 0; j < img->weigth; ++j)
{
for(int m = 0; m < iSize; ++m)
for(int n= 0; n< iSize; ++n)
{
...
}
}
這樣的演算法複雜度可以看出是為O(height*weigth*iSize^2)
然而使用分解後的一維函式進行兩次處理,程式應當如下:
for(int i = 0; i < img->height; ++i)
for(int j = 0; j < img->weigth; ++j)
{
for(int m = 0; m < iSize; ++m)
{
...
}
}
for(int j = 0; j< img->weigth; ++j)
for(int i= 0; i< img->height; ++i)
{
for(int m = 0; m < iSize; ++m)
{
...
}
}
這樣的演算法複雜度為O(2*height*weigth*iSize),比一維處理要少了很多,所以時間對應來說也會快一點。
用後者,我們的關鍵函式如下:
/*
生成一維高斯模板,水平的和垂直方向上的模板是一樣的
輸入引數分別是:模板大小,sigma值
輸出:一維陣列(高斯模板)
*/
double* CreateMuban(int iSize ,double sigma)
{
double *gauss = new double[iSize];//宣告一維模板
int radius = (iSize - 1) / 2;//這是高斯半徑
double MySigma = 2 * sigma * sigma;
double value = 0;
for (int i = 0; i < iSize; i++)
{//高斯函式前面的常數項因為在歸一化的時候將會消去,故這裡不重複計算
gauss[i] = exp(-(i - radius)*(i - radius)/MySigma);
value = value + gauss[i];
}
for (int i = 0; i < iSize; i++)
{//歸一化
gauss[i] = gauss[i] / value;
}
return gauss;
}
//對畫素進行操作
IplImage* operatorImage(IplImage* img, double* Muban, int iSize)
{
//建立一張新的圖片來進行濾波操作
IplImage* NewImage = cvCreateImage(cvSize(img->width, img->height), 8, 3);
int radius = (iSize - 1) / 2;
int r = 0;
int g = 0;
int b = 0;
CvScalar cs;
//複製圖片
cvCopy(img, NewImage);
//先對I,也就是垂直方向進行操作
for (int j = 0; j < NewImage->width; ++j)
{
for (int i = 0; i < NewImage->height; ++i)
{
//先判斷是否是邊緣,不是則操作,是則跳過不處理,保持原樣
if (!JudgeEdge(i, NewImage->height, radius))
{
for (int k = 0; k < iSize; ++k)
{
/* b = b + (int)((double)(NewImage->imageData + (i - radius + k) * NewImage->widthStep)[j * (int)NewImage->nChannels + 0] * Muban[k]);
g = g + (int)((double)(NewImage->imageData + (i - radius + k) * NewImage->widthStep)[j * (int)NewImage->nChannels + 1] * Muban[k]);
r = r + (int)((double)(NewImage->imageData + (i - radius + k) * NewImage->widthStep)[j * (int)NewImage->nChannels + 2] * Muban[k]); */
cs = cvGet2D(NewImage, i - radius + k, j); //獲取畫素
b = b + (int)((double)cs.val[0] * Muban[k]);
g = g + (int)((double)cs.val[1] * Muban[k]);
r = r + (int)((double)cs.val[2] * Muban[k]);
}
/*((uchar *)(NewImage->imageData + i * NewImage->widthStep))[j * NewImage->nChannels + 0] = b; //改變該畫素B的顏色分量
((uchar *)(NewImage->imageData + i * NewImage->widthStep))[j * NewImage->nChannels + 1] = g; //改變該畫素G的顏色分量
((uchar *)(NewImage->imageData + i * NewImage->widthStep))[j * NewImage->nChannels + 2] = r; //改變該畫素R的顏色分量 */
cs = cvGet2D(NewImage, i, j);
cs.val[0] = b;
cs.val[1] = g;
cs.val[2] = r;
cvSet2D(NewImage, i, j, cs);
b = 0;
g = 0;
r = 0;
}
}
}
//在對J,也就是水平方向進行操作
for (int i = 0; i < NewImage->height; ++i)
{
for (int j = 0; j < NewImage->width; ++j)
{
//先判斷是否是邊緣,不是則操作,是則跳過不處理,保持原樣
if (!JudgeEdge(j, NewImage->width, radius))
{
for (int k = 0; k < iSize; ++k)
{
/*b = b + (int)((double)(NewImage->imageData + i * NewImage->widthStep)[(j - radius + k) * (int)NewImage->nChannels + 0] * Muban[k]);
g = g + (int)((double)(NewImage->imageData + i * NewImage->widthStep)[(j - radius + k) * (int)NewImage->nChannels + 1] * Muban[k]);
r = r + (int)((double)(NewImage->imageData + i * NewImage->widthStep)[(j - radius + k) * (int)NewImage->nChannels + 2] * Muban[k]);*/
cs = cvGet2D(NewImage, i, j - radius + k); //獲取畫素
b = b + (int)((double)cs.val[0] * Muban[k]);
g = g + (int)((double)cs.val[1] * Muban[k]);
r = r + (int)((double)cs.val[2] * Muban[k]);
}
/*((uchar *)(NewImage->imageData + i * NewImage->widthStep))[j * NewImage->nChannels + 0] = b; //改變該畫素B的顏色分量
((uchar *)(NewImage->imageData + i * NewImage->widthStep))[j * NewImage->nChannels + 1] = g; //改變該畫素G的顏色分量
((uchar *)(NewImage->imageData + i * NewImage->widthStep))[j * NewImage->nChannels + 2] = r; //改變該畫素R的顏色分量*/
cs = cvGet2D(NewImage, i, j);
cs.val[0] = b;
cs.val[1] = g;
cs.val[2] = r;
cvSet2D(NewImage, i, j, cs);
b = 0;
g = 0;
r = 0;
//cout << r << " " << g << " " << b << endl;
}
}
}
return NewImage;
}
實現效果:
自己編的程式與openCV函式處理效果並無差別,成功!
最後,對高斯濾波部分進行擴充套件------自適應高斯濾波。為了達到更好的濾波效果,我們的手法需要更加靈活,往往可以加上一些限制條件進行判斷是否需要處理。這一點很想PID控制中的選擇積分的方法(具體名字忘了···囧)。這個我將在後面進行適當地嘗試!
學習高斯濾波只是一個開始,但是學習其他的影象處理方法諸如此類,我要學會舉一反三,而且要實踐與理論緊密結合,真正做到知其甚解才好啊!