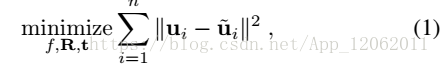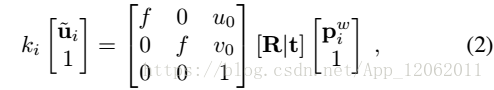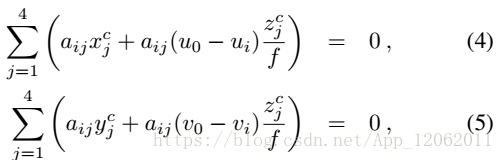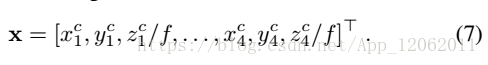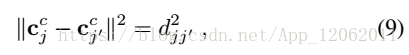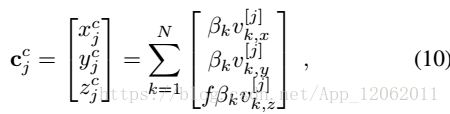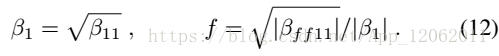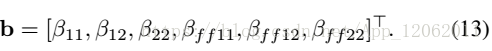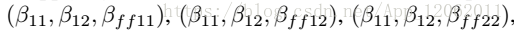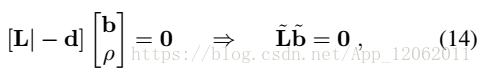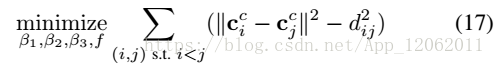論文：Exhaustive Linearization for Robust Camera Pose and Focal Length Estimation

整體來看，UPnP跟EPnP差不多，只是同時估計了焦距，因此，適合未標定場合，Uncalibrated PnP.

問題定義:

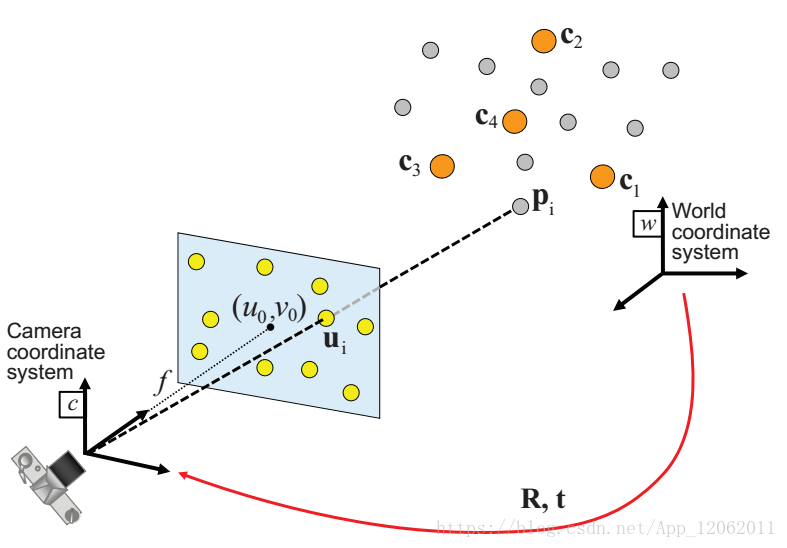
p世界座標系點參考點，C控制點，R，t姿態矩陣，u是p對應的2D投射點。建模為最小化P點的投影誤差。

其中u表示為：

k是尺度因子。 

 跟EPnP類似，增加控制點約束：

注意，這裡如上圖所示，c是在世界座標系下。同樣，相機座標系下，c的上標變為c。

3式帶入2式，展開得：

到這裡，跟EPnP的差別在於焦距， 本質 是一樣的，也得到線性方程組：

M也是2n*12的矩陣，得到x:

上面的方程中，四個控制點總共12個未知變數，M為2n×12的矩陣。因此，x屬於M的右零空間，vi為矩陣M的右奇異向量，可以通過求解MTM 的零空間特徵值得到。

[說明]使用MTM比使用M計算量更少，因為MTM是求解是常數複雜度，而M是O(n3)的複雜度，但是計算MTM的複雜度是O(n)的。

上面求解的x中，需要確定βk，也就是確定合適的線性組合。根據參考點的位置不同，矩陣MTM的零空間維數可能為N=1→4維。求解β的策略是控制點在座標系Fw和Fc中，兩兩之間的距離是相同，而x的3k+1−3k分量表示分別表示不同的控制點在相機座標系中的座標，總共有C24=6個約束。

同樣，也是分類討論。

N=1，線性化，此時只要求解β1和f，假定β11=β1^2，βff11=f^2β^2,根據控制點距離約束：

可以得到6個如下形式的方程：

其中b=[β11，βff11]T .

計算得到：

當N=2時，窮舉線性化，我們需要求β1，β2，f. 則類似N=1的情況，此時b變為：

與N=1類似，只是在相同的相機內外引數約束下，不斷窮舉，例如：

 當N=3時：窮舉再線性化。

再線性化技術如下：

以定義線性系統開始：

其中， 

具體演算法虛擬碼如下：

後面，為了提高精度，增加迭代優化：

完整的對比結果：

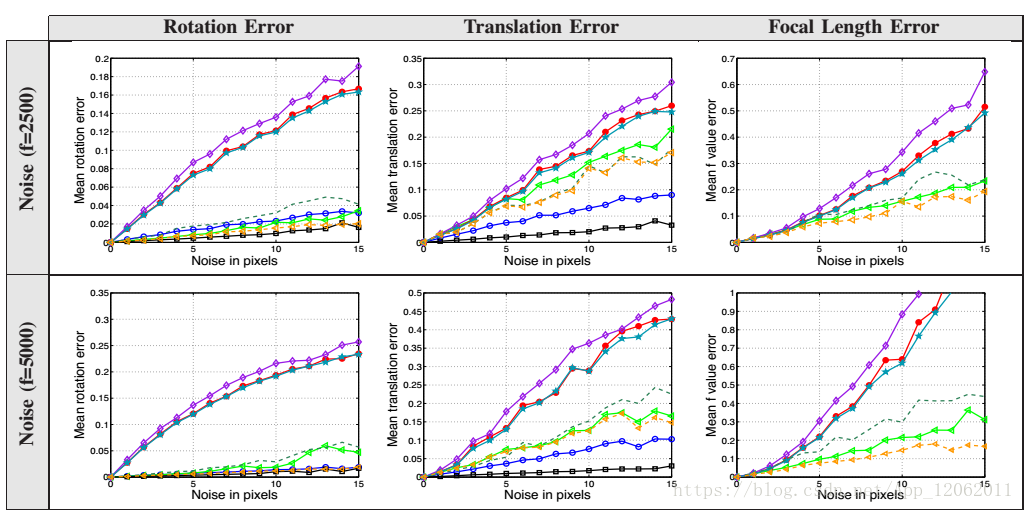
不共面：

上圖可以看出，在點數超過20時，其實UPnP與EPnP沒有太大差距，但是，UPnP更適合大焦距影象的姿態估計。當f>4000時，差距就出現了，但一般常見的f在500~2000之間，也就是近似估計為480i~1080p範圍。在這種情況下，EPnP與UPnP效能差不多。 

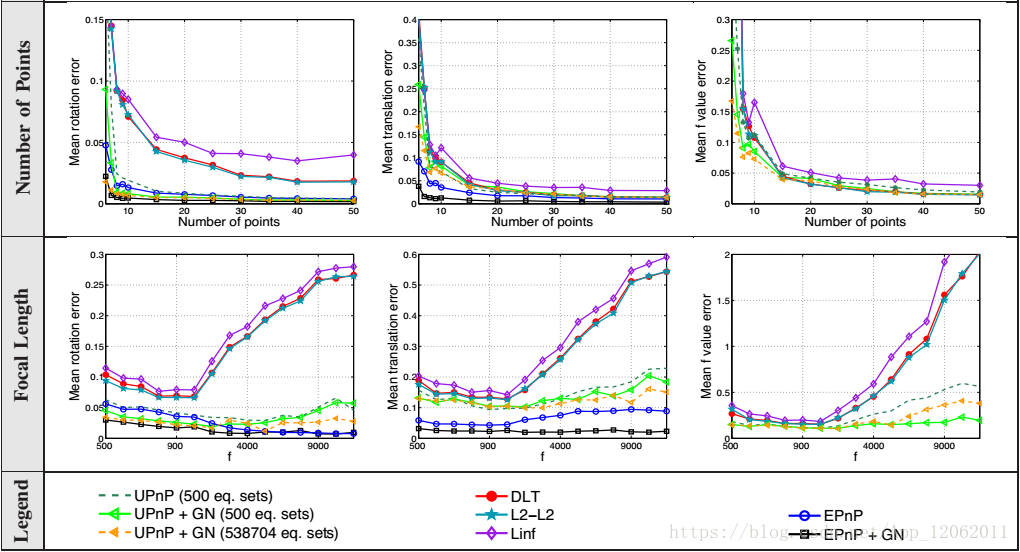
共面：

共面情況下，結論也類似，2者差距不大。

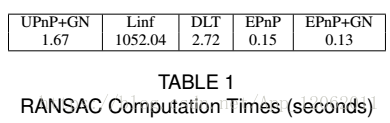
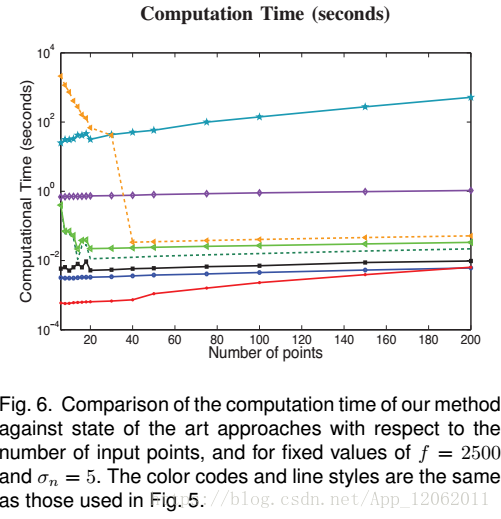
順便提一下時間：

作者在實測一個任務時，得到的結果如下：

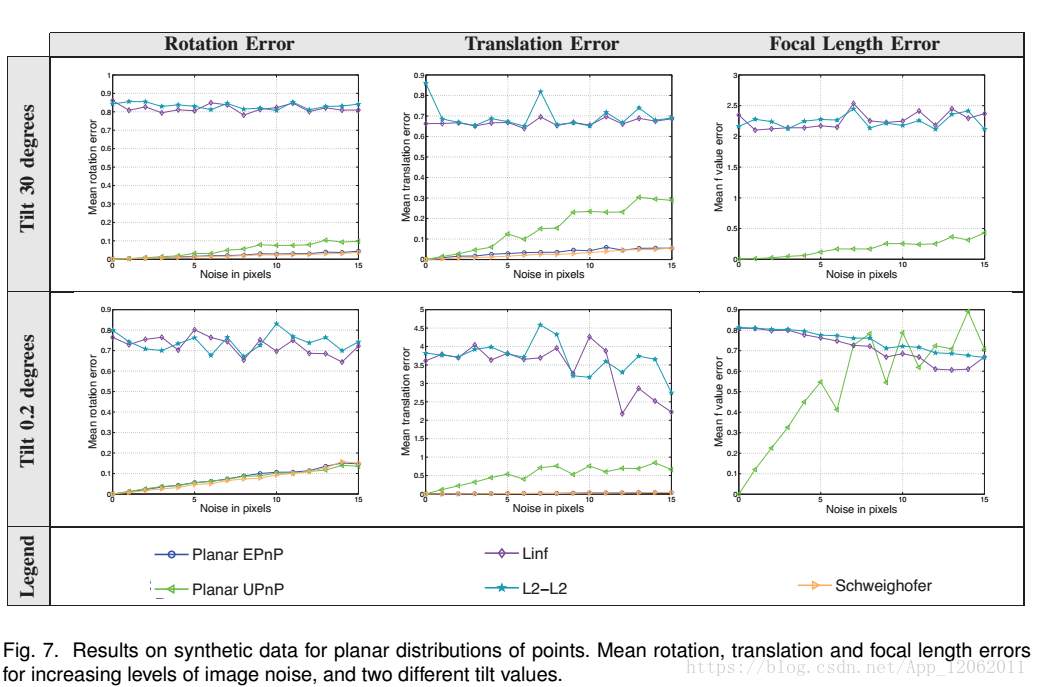
另外：

其中顏色標註對應上面不共面情況下的演算法類別。 

可以看到，UPnP在時間上跟EPnP比，是沒有優勢的。