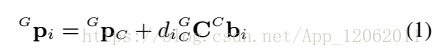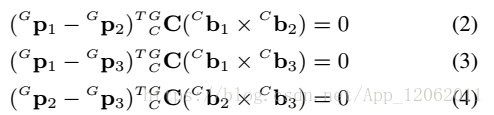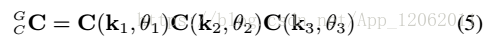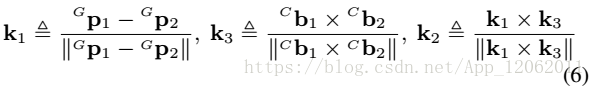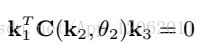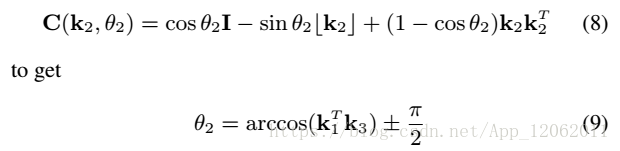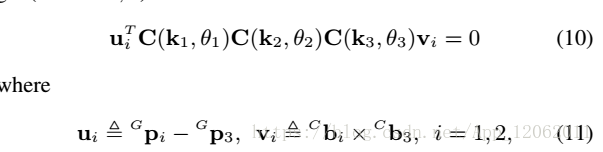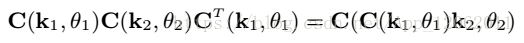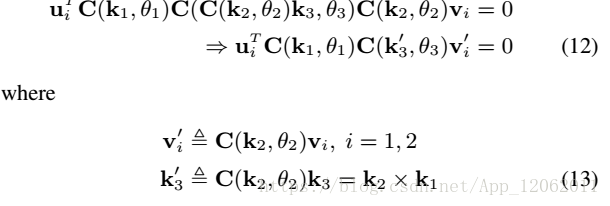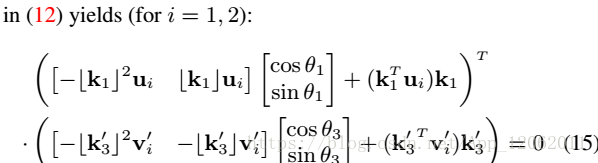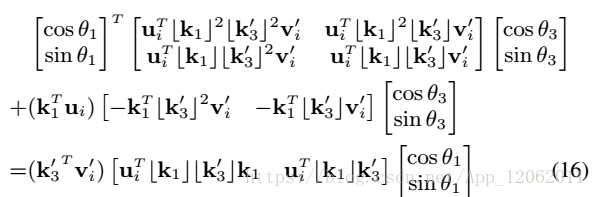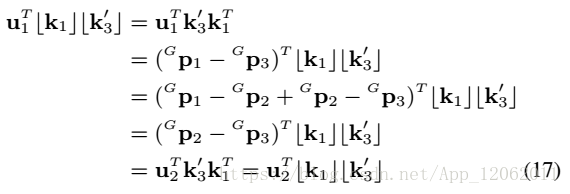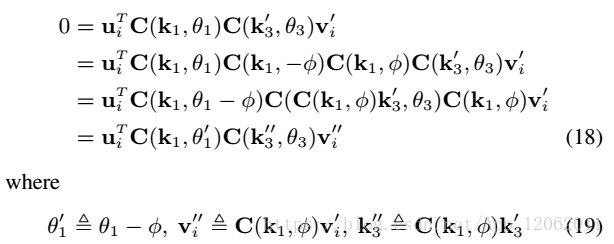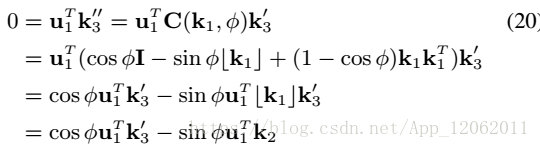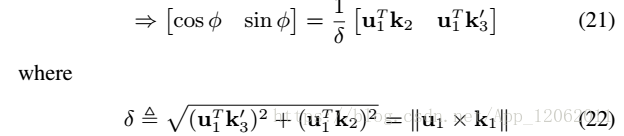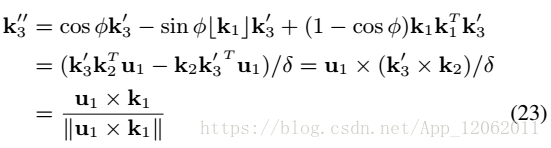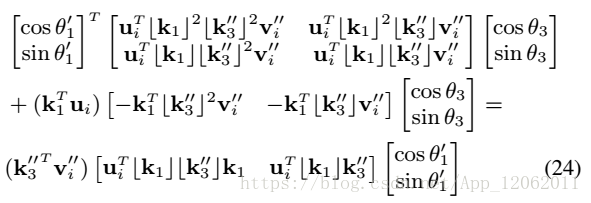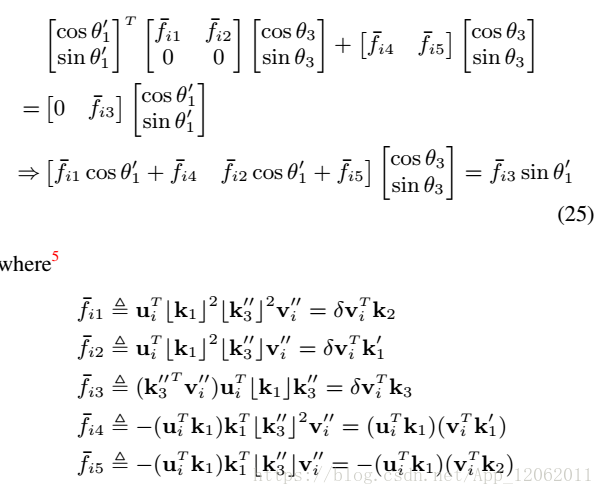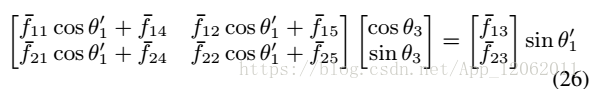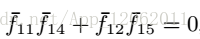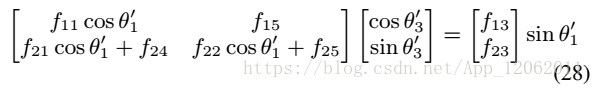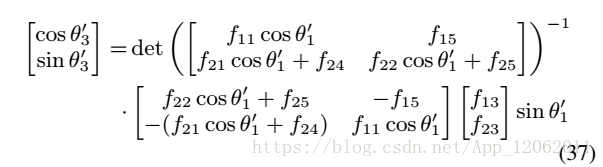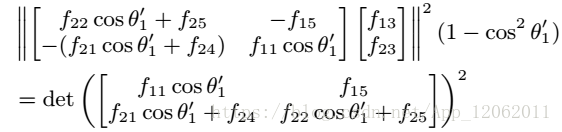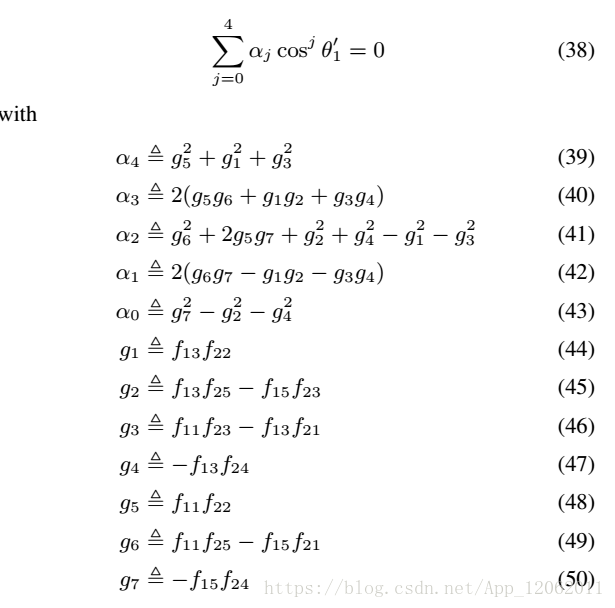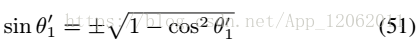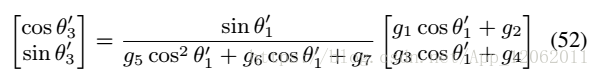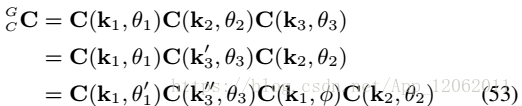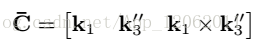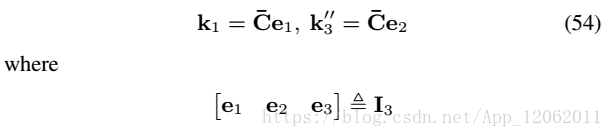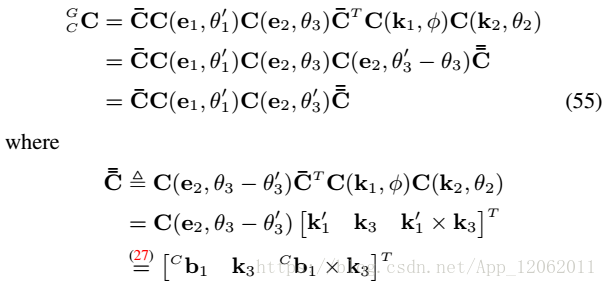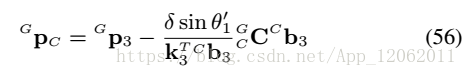AP3P

論文：An Efficient Algebraic Solution to the Perspective-Three-Point Problem

從數學的角度，提出了經典P3P演算法的更快，更魯棒，更準確的求解演算法。根據已知3對點，可以計算相機位姿和引數。

問題定義：

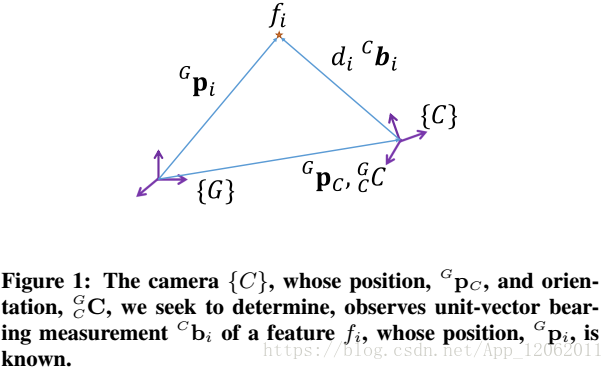
給定特徵fi i = 1, 2, 3在參考座標系中的位置,以及特徵點在相機座標系中的方向測量向量，目標是估計相機的旋轉矩陣和位置。其中C表示相機座標系，G表示 參考座標系。

根據幾何關係，我們得出：

其中di表示參考座標系中相機到特徵點的歐式距離，兩兩相減，並投影到對應面的法向量：

為了計算旋轉矩陣中的角度，我們定義如下因子分解：

其中： 

將式子5代替到公式2中，得到標量方程：（未知）

然後利用羅德里格斯變換:

為了求其他兩個角度，定義如下因子分解：

利用旋轉矩陣特性：

化簡式10：

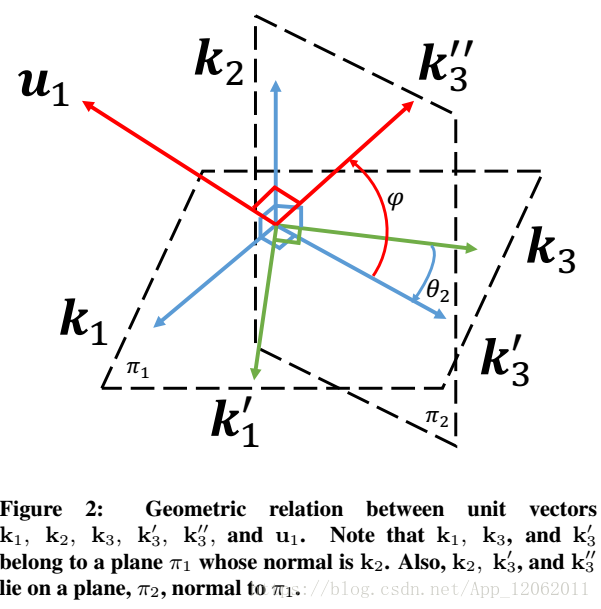
式13表述的幾何關係下圖所示：

接著，再次採用羅德里格斯變換得到：

展開並重排上式：

 其中：

出現3次，由此，我們重寫式12：

 為了化簡等價於16式的18式，我們尋找一個，使得下式成立：

推出：

然後，根據19、8式得到：

接著，利用14式，展開18式，得到一個16式的等價結果：

 在24式中，代替17式為0，並重排結果：

帶入具體的i = 1，2到式25，得到：

因為：

繼續化簡式26，同時 引入新引數：

然後用代替：

 根據28式，得到：

計算兩邊的歸一化結果：

得到一個關於的4階多項式.更加簡潔的表達如下：

剩下的就是如何計算的問題了，作者採用，逼近的方式找到式38的近似解，一旦找到式38的4個解，便採用牛頓方法進行優化，以最小代價提高精度。

另外，要注意的是：

對於每個cos，可能會得到2個sin值，如下：

這會導致計算出2個旋轉矩陣， 因此，借用di>0,可以排除一個無效的。下一步，根據每對（cos ，sin ），計算（cos ，sin ），利用式37：

最後，根據19、27，5，我們找到相機位置，也可以利用5，12，18式，更快速得到：

 我們定義如下旋轉矩陣：

因此：

 將式54帶入53，得：

接著，計算相機位置：

這裡，為了速度，只計算了一個點i=3,如果更在意精度，可以用最小二乘擬合i=1,2,3點的結果。

最後，AP3P已經在OpenCV3中實現了。