我們要找的是一個概率。

f即x屬於C1的機率。

上面的過程就是logistic regression。

下面將logistic regression與linear regression作比較。

接下來訓練模型，看看模型的好壞。

假設有N組training data，如上藍框中顯示，x1屬於C1，其他類推。假設這組training data是從函式產生的。

給我們一組w和b，我們就可以決定函式。

某一組w和b，產生N組training data的機率怎麼計算？

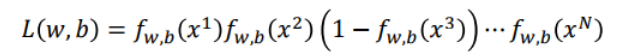
假設x3屬於C2，則就有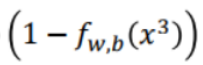，其他以此類推。

有最大可能性可以產生這組training data的w和b我們叫做

這其實就是概率論與數理統計中的最大似然估計。

我們可以把似然函式寫成對數似然函式，這樣更好計算。取ln後上面的相乘式就變成了相加式。

即

加上負號，那麼就從找似然函式的最大值變成找對數似然函式的最小值。

如果某個xi屬於class1，我們就說它的target是1，如果它屬於class2，我們就說它的target是0。

於是對數似然函式可以寫成：

注意從左邊到右邊的寫法實際上是交叉熵。

上面的展開式我們可以寫成：

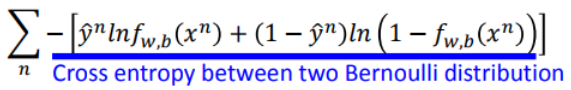
這就是交叉熵。（實際上是兩個伯努利分佈的交叉熵）

即：假設有兩個伯努利分佈p和q如下：

則p和q的交叉熵為：

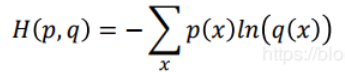
那麼在logistic regression中如何定義function的好壞？

我們使用上面的交叉熵函式作為loss function來確定函式的好壞。

為什麼要用交叉熵函式作為loss function而不用方差和的平均值？

個人的理解是，logistic regression的輸出經過了sigmoid函式的處理，使得輸出值都在(0,1)之間；而linear regression的輸出可以是任何值（不限制區間），因此如果logistic regression的loss function使用方差和的平均值的話，其loss值就會很小。效果不太好。

下面我們要找一個最好的function。

整理一下，結果為：

接下來我們繼續比較linear regression和logistic regression更新引數的方式：

我們可以發現它們更新引數的方式是一模一樣的。唯一不同的是，logistic regression的一定是0或1，的值一定在(0,1)內。

logistic regression如果用squaer Error作為loss函式會怎麼樣？

這時候如果你離目標很近或很遠時，其梯度算出來都是0。這時對class1的例子，如果對class2，結果也一樣。

如果我們把loss值變化做成圖，如下：

如果用Square Error作為loss function，那麼無論是離最低點很近或很遠時其梯度都接近0，引數更新會非常慢。

如果用cross entropy作為loss function，那麼離的遠時梯度大，離的近時梯度小。

所以我們要用cross entropy。

我們可以發現linear regression和logistic regression的model是一樣的。

不同的是logistic regression的輸出用sigmoid函式作了處理。

雖然是同一種model的形式，但是因為我們作了不同的假設，我們根據同一組training data找出來的w和b也不一樣。

如果我們比較生成模型和判別模型：

為什麼我們會覺得discriminative model比generative model更好？

我們舉一個例子。

class1只收集到1筆data，class2共收集到12筆data。

這時給出圖上的testing data，你覺得它是class1或2？

我們看看貝葉斯公式：

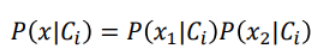
我們來根據training data統計一下機率：

現在我們計算test data屬於class1的機率。

結果小於0.5。也就是說用貝葉斯公式的話，機器會認為這個test data屬於class1的機率小於0.5。

為什麼會這樣？因為對貝葉斯公式，各個樣本都是獨立的。

如果我們用logistic regression（屬於discriminative model），我們會認為test data屬於class1的機率更大。

如果我們用generative model，如上面的貝葉斯公式，由於generative model要做種種的假設，最後反而計算出test data屬於class2的機率更大。當然，這種判斷不一定是錯的。

如果train data很少時，使用generative model可以得到更準確的判斷；

如果model中的train data中noise較多時，使用discriminative model的判斷更準確。

換句話說，在某些應用場景中，我們可以確定資料的來自哪個分佈的先驗概率。這種情況下discriminative model的判斷更準確。

下面看看Multi-class Classification。

這個時候我們使用softmax函式對輸出做處理。

如果只有二分類的情況下使用softmax就退化成logistic regression的情況。

logistic regression的限制：

如果有上面這一組train data，這時候我們可以發現，我們無法用一條直線將所有的紅點的z>0，藍點z<0分辨劃分在直線的兩邊。

這時怎麼辦呢？我們可以對原來的featrue做一下轉換：

但是feature transformation的函式不是很好找，轉換了也不一定就能夠找出一個合適的logistic regression。

feature transformation可以看成多個logistic regression的重疊。

這個其實就是多層感知機。

即x1和x2通過藍色和綠色的logistic regression先處理生成x1',x2'。

現在我們給藍色和綠色的logistic regression各假設一組引數。計算出的結果如下圖右邊的圖。

接下來紅色的logistic regression的輸入就是x1',x2'。

上面的這個結構就是deep learning中的神經元結構。由許多神經元結構組成一個神經網路。

這就是deep learning。