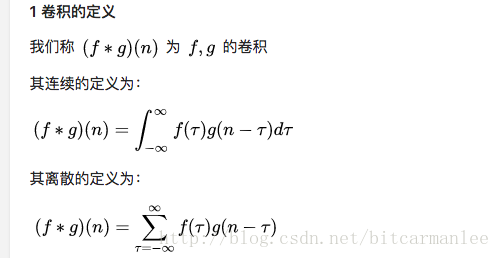最近在看影象處理，卷積運算這一塊也查了很多，但是感覺都寫的太複雜，我這裡簡單的寫一下卷積到底是一個什麼計算過程。

假設有一個卷積核h，就一般為3*3的矩陣：

有一個待處理矩陣x：

h*x的計算過程分為三步

第一步，將卷積核翻轉180°，也就是成為了

第二步，將卷積核h的中心對準x的第一個元素，然後對應元素相乘後相加，沒有元素的地方補0。

這樣結果Y中的第一個元素值Y11=1*0+2*0+1*0+0*0+0*1+0*2+-1*0+-2*5+-1*6=-16

第三步每個元素都像這樣計算出來就可以得到一個輸出矩陣，就是卷積結果

……………………

像這樣計算，其他過程略了。

最後結果

注意：

我這裡是用0補全原矩陣的，但我們不一定選擇0。在Opencv的cvFilter2D函式中，就沒有使用0來補全矩陣，而是用了邊緣拷貝的方式

補充

另外在知乎上看到非常好也非常生動形象的解釋，特意複製貼上過來。(知乎馬同學的解釋)

從數學上講，卷積就是一種運算。
某種運算，能被定義出來，至少有以下特徵：
1.首先是抽象的、符號化的
2.其次，在生活、科研中，有著廣泛的作用

比如加法：
1.a+b，是抽象的，本身只是一個數學符號
2.在現實中，有非常多的意義，比如增加、合成、旋轉等等

卷積，是我們學習高等數學之後，新接觸的一種運算，因為涉及到積分、級數，所以看起來覺得很複雜。

這兩個式子有一個共同的特徵：

這個特徵有什麼意義？

只看數學符號，卷積是抽象的，不好理解的，但是，我們可以通過現實中的意義，來習慣卷積這種運算，正如我們小學的時候，學習加減乘除需要各種蘋果、糖果來幫助我們習慣一樣。

我們來看看現實中，這樣的定義有什麼意義。

2 離散卷積的例子：丟骰子

我有兩枚骰子：

把這兩枚骰子都丟擲去：

求：兩枚骰子點數加起來為4的概率是多少?
這裡問題的關鍵是，兩個骰子加起來要等於4，這正是卷積的應用場景。

我們把骰子各個點數出現的概率表示出來：

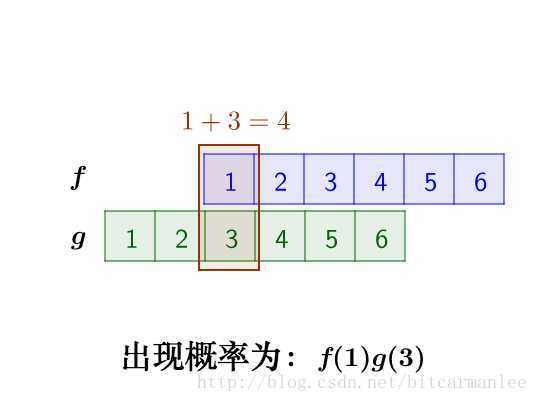
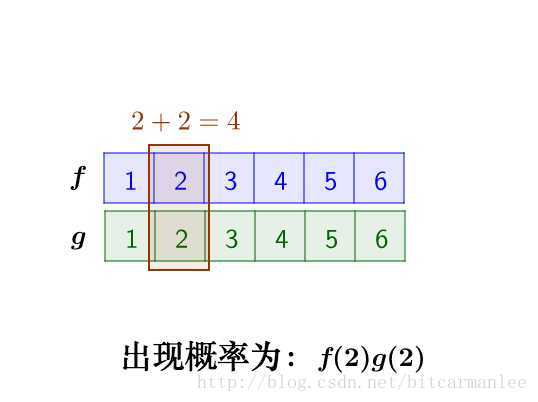
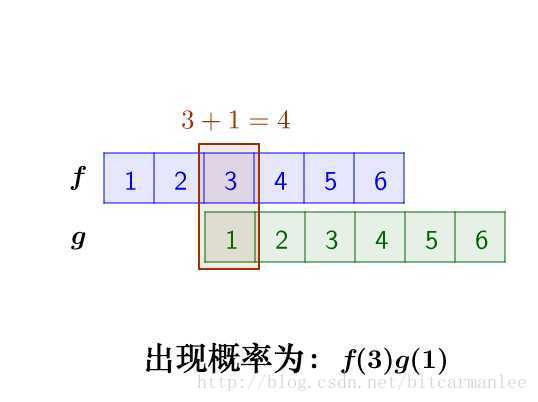
那麼，兩枚骰子點數加起來為4的情況有：

因此，兩枚骰子點數加起來為4的概率為：
f(1)g(3)+f(2)g(2)+f(3)g(1)

符合卷積的定義，把它寫成標準的形式就是：

(f∗g)(4)=∑m=13f(4−m)g(m)

3 連續卷積的例子：做饅頭

樓下早點鋪子生意太好了，供不應求，就買了一臺機器，不斷的生產饅頭。
假設饅頭的生產速度是 f(t) ，那麼一天後生產出來的饅頭總量為：
∫240f(t)dt

饅頭生產出來之後，就會慢慢腐敗，假設腐敗函式為 g(t) ，比如，10個饅頭，24小時會腐敗：
10∗g(t)
想想就知道，第一個小時生產出來的饅頭，一天後會經歷24小時的腐敗，第二個小時生產出來的饅頭，一天後會經歷23小時的腐敗。
如此，我們可以知道，一天後，饅頭總共腐敗了：
∫240f(t)g(24−t)dt
這就是連續的卷積。