卷積這個東東是“訊號與系統”中論述系統對輸入訊號的響應而提出的。因為是對模擬訊號論述的，所

以常常帶有繁瑣的算術推倒，很簡單的問題的本質常常就被一大堆公式淹沒了，那麼卷積究竟物理意義

怎麼樣呢？

卷積表示為y(n) = x(n)*h(n)

使用離散數列來理解卷積會更形象一點，我們把y(n)的序列表示成y(0),y(1),y(2) and so on; 這是系

統響應出來的訊號。

同理，x(n)的對應時刻的序列為x(0),x(1),x(2)...and so on;

其實我們如果沒有學過訊號與系統，就常識來講，系統的響應不僅與當前時刻系統的輸入有關，也跟之

前若干時刻的輸入有關，因為我們可以理解為這是之前時刻的輸入訊號經過一種過程（這種過程可以是

遞減，削弱，或其他）對現在時刻系統輸出的影響，那麼顯然，我們計算系統輸出時就必須考慮現在時

刻的訊號輸入的響應以及之前若干時刻訊號輸入的響應之“殘留”影響的一個疊加效果。

假設0時刻系統響應為y(0),若其在1時刻時，此種響應未改變，則1時刻的響應就變成了y(0)+y(1),叫序

列的累加和（與序列的和不一樣）。但常常系統中不是這樣的，因為0時刻的響應不太可能在1時刻仍舊

未變化，那麼怎麼表述這種變化呢，就通過h(t)這個響應函式與x(0)相乘來表述，表述為x(m)×h(m-n)

，具體表達式不用多管，只要記著有大概這種關係，引入這個函式就能夠表述y(0)在1時刻究竟削弱了多

少，然後削弱後的值才是y(0)在1時刻的真實值，再通過累加和運算，才得到真實的系統響應。

再拓展點，某時刻的系統響應往往不一定是由當前時刻和前一時刻這兩個響應決定的，也可能是再加上

前前時刻，前前前時刻，前前前前時刻，等等，那麼怎麼約束這個範圍呢，就是通過對h(n)這個函式在

表示式中變化後的h(m-n)中的m的範圍來約束的。即說白了，就是當前時刻的系統響應與多少個之前時刻

的響應的“殘留影響”有關。

當考慮這些因素後，就可以描述成一個系統響應了，而這些因素通過一個表示式（卷積）即描述出來不

得不說是數學的巧妙和迷人之處了。

 ==================================================================================================

對於非數學系學生來說，只要懂怎麼用卷積就可以了，研究什麼是卷積其實意義不大,它就是一種微元相

乘累加的極限形式。卷積本身不過就是一種數學運算而已。就跟“蝶形運算”一樣，怎麼證明，這是數

學系的人的工作。
在訊號與系統裡，f(t)的零狀態響應y(t)可用f(t)與其單位衝激響應h(t) 的卷積積分求解得，即y(t)

=f(t)*h(t)。學過訊號與系統的都應該知道，時域的卷積等於頻域的乘積，即有 Y(s)=F(s)×H(s)。

（s=jw，拉氏變換後等到的函式其實就是訊號的頻域表示式）
有一點你必須明白，在通訊系統裡，我們關心的以及 要研究的是訊號的頻域，不是時域，原因是因為信

號的頻率是攜帶有資訊的量。
所以，我們需要的是Y(s)這個表示式，但是實際上，我們往往不能很容易的得到F(s)和H(s)這兩個表達

式，但是能直接的很容易的得到f(t)和h(t)，所以為了找到Y(s)和y(t)的對應關係，就要用到卷積運算

。
複頻域。
s=jw，當中的j是複數單位，所以使用的是複頻域。通俗的解釋方法是，因為系統中有電感X=jwL、電容

X=1/jwC，物理意義是，系統H(s)對不同的頻率分量有不同的衰減，即這種衰減是發生在頻域的，所以為

了與時域區別，引入複數的運算。但是在複頻域計算的形式仍然滿足歐姆定理、KCL、KVL、疊加法。
負的頻率。
之所以會出現負的頻率，這只是數學運算的結果，只存在於數學運算 中，實際中不會有負的頻率。

卷積的過程就是相當於把訊號分解為無窮多的衝擊訊號，
然後進行衝擊響應的疊加。
 
有一個七品縣令，喜歡用打板子來懲戒那些市井無賴，而且有個慣例：如果沒犯大罪，只打一板，釋放

回家，以示愛民如子。

有一個無賴，想出人頭地卻沒啥指望，心想：既然揚不了善名，出惡名也成啊。怎麼出惡名？炒作唄！

怎麼炒作？找名人呀！他自然想到了他的行政長官——縣令。

無賴於是光天化日之下，站在縣衙門前撒了一泡尿，後果是可想而知地，自然被請進大堂捱了一板子，

然後昂首挺胸回家，躺了一天，嘿！身上啥事也沒有！第二天如法炮製，全然不顧行政長管的仁慈和衙

門的體面，第三天、第四天......每天去縣衙門領一個板子回來，還喜氣洋洋地，堅持一個月之久！這

無賴的名氣已經和衙門口的臭氣一樣，傳遍八方了！

縣令大人噤著鼻子，呆呆地盯著案子上的驚堂木，擰著眉頭思考一個問題：這三十個大板子怎麼不好使

捏？......想當初，本老爺金榜題名時，數學可是得了滿分，今天好歹要解決這個問題：

——人（系統！）挨板子（脈衝！）以後，會有什麼表現（輸出！）？

——費話，疼唄！

——我問的是：會有什麼表現？

——看疼到啥程度。像這無賴的體格，每天挨一個板子啥事都不會有，連哼一下都不可能，你也看到他

那得意洋洋的嘴臉了（輸出0）；如果一次連揍他十個板子，他可能會皺皺眉頭，咬咬牙，硬挺著不哼（

輸出1）；揍到二十個板子，他會疼得臉部扭曲，象豬似地哼哼（輸出3）；揍到三十個板子，他可能會

象驢似地嚎叫，一把鼻涕一把淚地求你饒他一命（輸出5）；揍到四十個板子，他會大小便失禁，勉強哼

出聲來（輸出1）；揍到五十個板子，他連哼一下都不可能（輸出0）—— 死啦！

縣令鋪開座標紙，以打板子的個數作為X軸，以哼哼的程度（輸出）為Y軸，繪製了一條曲線：

——嗚呼呀！這曲線象一座高山，弄不懂弄不懂。為啥那個無賴連捱了三十天大板卻不喊繞命呀？

——呵呵，你打一次的時間間隔（Δτ=24小時）太長了，所以那個無賴承受的痛苦程度一天一利索，沒

有疊加，始終是一個常數；如果縮短打板子的時間間隔（建議Δτ=0.5秒），那他的痛苦程度可就迅速

疊加了；等到這無賴挨三十個大板（t=30）時，痛苦程度達到了他能喊叫的極限，會收到最好的懲戒效

果，再多打就顯示不出您的仁慈了。

——還是不太明白，時間間隔小，為什麼痛苦程度會疊加呢？

——這與人（線性時不變系統）對板子（脈衝、輸入、激勵）的響應有關。什麼是響應？人挨一個板子

後，疼痛的感覺會在一天（假設的，因人而異）內慢慢消失（衰減），而不可能突然消失。這樣一來，

只要打板子的時間間隔很小，每一個板子引起的疼痛都來不及完全衰減，都會對最終的痛苦程度有不同

的貢獻：

t個大板子造成的痛苦程度=Σ(第τ個大板子引起的痛苦*衰減係數)[衰減係數是（t-τ）的函式，仔細

品味]

數學表達為：y(t)=∫T(τ)H(t-τ)

——拿人的痛苦來說卷積的事，太殘忍了。除了人以外，其他事物也符合這條規律嗎？

——呵呵，縣令大人畢竟仁慈。其實除人之外，很多事情也遵循此道。好好想一想，鐵絲為什麼彎曲一

次不折，快速彎曲多次卻會輕易折掉呢？

——恩，一時還弄不清，容本官慢慢想來——但有一點是明確地——來人啊，將撒尿的那個無賴抓來，

狠打40大板！

作者：果程C
連結：https://www.zhihu.com/question/22298352/answer/50940942
來源：知乎
著作權歸作者所有，轉載請聯絡作者獲得授權。

對於初學者，我推薦用複利的例子來理解卷積可能更好理解一些：

小明存入100元錢，年利率是5%，按複利計算（即將每一年所獲利息加入本金，以計算下一年的利息），那麼在五年之後他能拿到的錢數是，如下表所示：
<img src="https://pic2.zhimg.com/5fa86c80c31dd277d038527555aa4d75_b.jpg" data-rawwidth="1293" data-rawheight="95" class="origin_image zh-lightbox-thumb" width="1293" data-original="https://pic2.zhimg.com/5fa86c80c31dd277d038527555aa4d75_r.jpg">將這筆錢存入銀行的一年之後，小明又往銀行中存入了100元錢，年利率仍為5%，那麼這筆錢按複利計算，到了第五年，將收回的錢數是將這筆錢存入銀行的一年之後，小明又往銀行中存入了100元錢，年利率仍為5%，那麼這筆錢按複利計算，到了第五年，將收回的錢數是，我們將這一結果作為新的一行加入上面的表格中：
<img src="https://pic4.zhimg.com/39f37df8c96d7219cba5d081919a3a2f_b.jpg" data-rawwidth="1296" data-rawheight="134" class="origin_image zh-lightbox-thumb" width="1296" data-original="https://pic4.zhimg.com/39f37df8c96d7219cba5d081919a3a2f_r.jpg">以此類推，如果小明每年都往銀行中存入新的100元錢，那麼這個收益表格將是這樣的：以此類推，如果小明每年都往銀行中存入新的100元錢，那麼這個收益表格將是這樣的：
<img src="https://pic2.zhimg.com/cfe98b9d33640fae02a21bf369f0459d_b.jpg" data-rawwidth="1296" data-rawheight="284" class="origin_image zh-lightbox-thumb" width="1296" data-original="https://pic2.zhimg.com/cfe98b9d33640fae02a21bf369f0459d_r.jpg">可見，最終小明拿到的錢將等於他各年存入的錢分別計算複利之後得到的錢數的總和，即：可見，最終小明拿到的錢將等於他各年存入的錢分別計算複利之後得到的錢數的總和，即：
<img src="https://pic3.zhimg.com/fba65159d3472936979002b01b606a0e_b.jpg" data-rawwidth="1077" data-rawheight="124" class="origin_image zh-lightbox-thumb" width="1077" data-original="https://pic3.zhimg.com/fba65159d3472936979002b01b606a0e_r.jpg">用求和符號來簡化這個公式，可以得到：用求和符號來簡化這個公式，可以得到：

在上式中，為小明的存錢函式，而為存入銀行的每一筆錢的複利計算函式。在這裡，小明最終得到的錢就是他的存錢函式和複利計算函式的卷積。
為了更清晰地看到這一點，我們將這個公式推廣到連續的情況，也就是說，小明在從到的這一段時間內，每時每刻都往銀行裡存錢，他的存錢函式為，而銀行也對他存入的每一筆錢按複利公式計算收益：，則小明到時間將得到的總錢數為：

這也就是卷積的表示式了，上式可以記為。

相信通過上面這個例子，大家應該能夠很清晰地記住卷積公式了。下面我們再展開說兩句：
如果我們將小明的存款函式視為一個訊號發生（也就是激勵）的過程，而將複利函式視為一個系統對訊號的響應函式（也就是響應），那麼二者的卷積就可以看做是在時刻對系統進行觀察，得到的觀察結果（也就是輸出）將是過去產生的所有訊號經過系統的「處理／響應」後得到的結果的疊加，這也就是卷積的物理意義了。
作者：匿名使用者
連結：https://www.zhihu.com/question/22298352/answer/34267457
來源：知乎
著作權歸作者所有，轉載請聯絡作者獲得授權。

有那麼麻煩嗎？
不推薦用“反轉/翻轉/反褶/對稱”等解釋卷積。好好的訊號為什麼要翻轉？導致學生難以理解卷積的物理意義。
這個其實非常簡單的概念，國內的大多數教材卻沒有講透。

直接看圖，不信看不懂。以離散訊號為例，連續訊號同理。

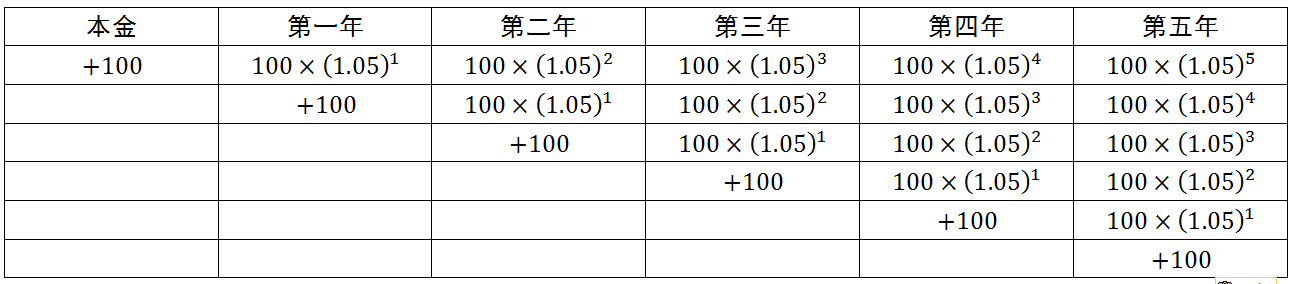
已知
<img src="https://pic4.zhimg.com/153fd3e7911d486edaf0475afb1e54b3_b.png" data-rawwidth="600" data-rawheight="214" class="origin_image zh-lightbox-thumb" width="600" data-original="https://pic4.zhimg.com/153fd3e7911d486edaf0475afb1e54b3_r.png">

已知
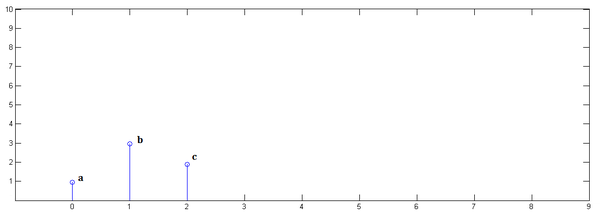
<img src="https://pic3.zhimg.com/c47d9d7f7a29c491782bf7b1baea3f8e_b.png" data-rawwidth="600" data-rawheight="214" class="origin_image zh-lightbox-thumb" width="600" data-original="https://pic3.zhimg.com/c47d9d7f7a29c491782bf7b1baea3f8e_r.png">

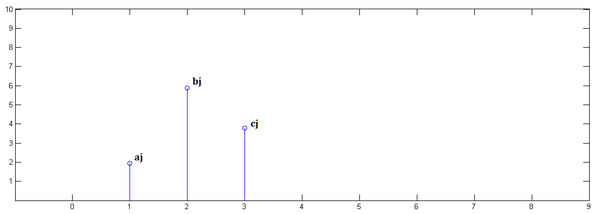
下面通過演示求的過程，揭示卷積的物理意義。

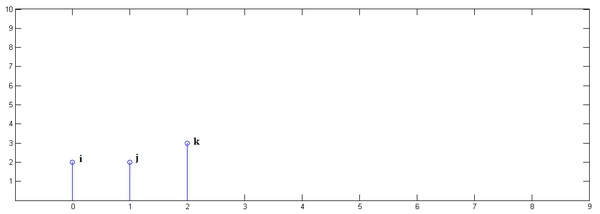
第一步，乘以並平移到位置0：
<img src="https://pic1.zhimg.com/91f5eff235013ac729c44e98b3a537d0_b.png" data-rawwidth="600" data-rawheight="214" class="origin_image zh-lightbox-thumb" width="600" data-original="https://pic1.zhimg.com/91f5eff235013ac729c44e98b3a537d0_r.png">
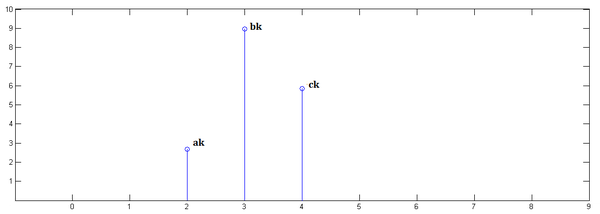
第二步，乘以並平移到位置1：
<img src="https://pic1.zhimg.com/67c05239b05f671766b9df9393026f2c_b.png" data-rawwidth="600" data-rawheight="214" class="origin_image zh-lightbox-thumb" width="600" data-original="https://pic1.zhimg.com/67c05239b05f671766b9df9393026f2c_r.png">
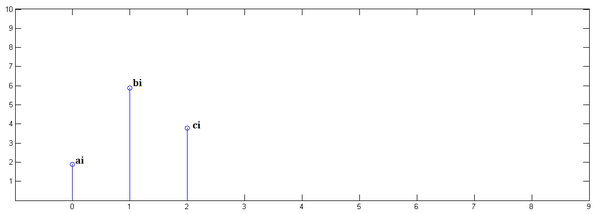
第三步，乘以並平移到位置2：
<img src="https://pic2.zhimg.com/c34e839a49c6b616c57bde3c3dbbd67d_b.png" data-rawwidth="600" data-rawheight="214" class="origin_image zh-lightbox-thumb" width="600" data-original="https://pic2.zhimg.com/c34e839a49c6b616c57bde3c3dbbd67d_r.png">
最後，把上面三個圖疊加，就得到了：
<img src="https://pic3.zhimg.com/4ce6cdcc28b10aca73db3f877d86ca02_b.png" data-rawwidth="600" data-rawheight="313" class="origin_image zh-lightbox-thumb" width="600" data-original="https://pic3.zhimg.com/4ce6cdcc28b10aca73db3f877d86ca02_r.png">
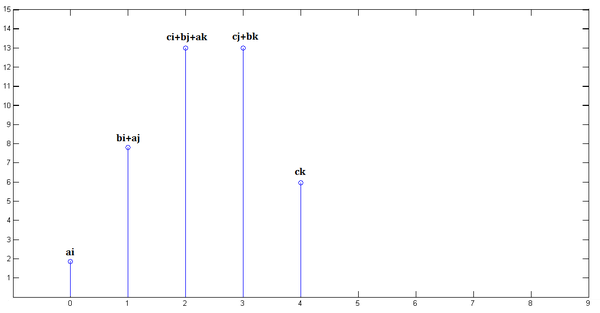
簡單吧？無非是平移（沒有反褶！）、疊加。

====================================================

從這裡，可以看到卷積的重要的物理意義是：一個函式（如：單位響應）在另一個函式（如：輸入訊號）上的加權疊加。


重複一遍，這就是卷積的意義：加權疊加。

對於線性時不變系統，如果知道該系統的單位響應，那麼將單位響應和輸入訊號求卷積，就相當於把輸入訊號的各個時間點的單位響應 加權疊加，就直接得到了輸出訊號。


通俗的說：
在輸入訊號的每個位置，疊加一個單位響應，就得到了輸出訊號。
這正是單位響應是如此重要的原因。

在輸入訊號的每個位置，疊加一個單位響應，就得到了輸出訊號。
這正是單位響應是如此重要的原因。

在輸入訊號的每個位置，疊加一個單位響應，就得到了輸出訊號。
這正是單位響應是如此重要的原因。