172322 2018-2019-1 《程式設計與資料結構》實驗二報告
阿新 • • 發佈:2018-11-11
172322 2018-2019-1 《程式設計與資料結構》實驗二報告
- 課程:《程式設計與資料結構》
- 班級: 1723
- 姓名: 張昊然
- 學號:20172322
- 實驗教師:王志強
- 助教:張之睿/張師瑜
- 實驗日期:2018年11月10日
- 必修/選修: 必修
1.實驗內容
- 此處填寫實驗的具體內容:
實驗內容過多,故參考作業:
- 實驗二-1-實現二叉樹
- 參考教材p212,完成鏈樹LinkedBinaryTree的實現(getRight,contains,toString,preorder,postorder), 用JUnit或自己編寫驅動類對自己實現的LinkedBinaryTree進行測試,提交測試程式碼執行截圖,要全屏,包含自己的學號資訊。
- 實驗二 樹-2-中序先序序列構造二叉樹
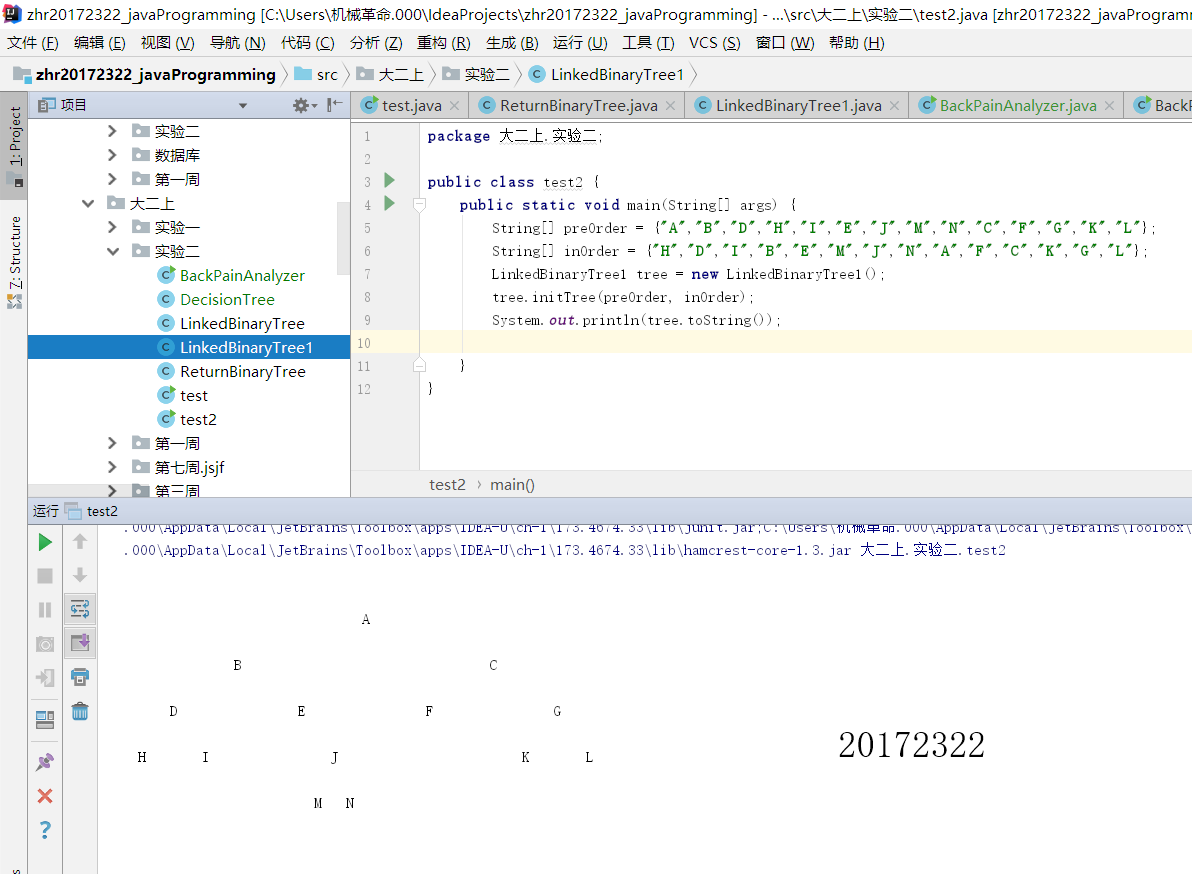
- 基於LinkedBinaryTree,實現基於(中序,先序)序列構造唯一一棵二㕚樹的功能,比如給出中序HDIBEMJNAFCKGL和後序ABDHIEJMNCFGKL,構造出附圖中的樹,用JUnit或自己編寫驅動類對自己實現的功能進行測試,提交測試程式碼執行截圖,要全屏,包含自己的學號資訊
- 實驗二 樹-3-決策樹
- 自己設計並實現一顆決策樹
- 實驗二 樹-4-表示式樹
- 輸入中綴表示式,使用樹將中綴表示式轉換為字尾表示式,並輸出字尾表示式和計算結果(如果沒有用樹,則為0分)
- 實驗二 樹-5-二叉查詢樹
- 完成PP11.3
- 實驗二 樹-6-紅黑樹分析
- 參考http://www.cnblogs.com/rocedu/p/7483915.html對Java中的紅黑樹(TreeMap,HashMap)進行原始碼分析,並在實驗報告中體現分析結果。
2.實驗過程及結果
過程:
- 本次實驗總共五個提交點。我也分為五個部分來寫過程。
- 第一:要求實現
getRight,contains,toString,preorder,postorder,這些分別是得到右孩子,是否包含,輸出,前序遍歷,後續遍歷,關鍵程式碼如下:
public LinkedBinaryTree1<T> getRight() { if(root == null) { throw new EmptyCollectionException("BinaryTree"); } LinkedBinaryTree1<T> result = new LinkedBinaryTree1<>(); result.root = root.getRight(); return result; public boolean contains(T targetElement) { BinaryTreeNode node = root; BinaryTreeNode temp = root; boolean result = false; if (node == null){ result = false; } if (node.getElement().equals(targetElement)){ result = true; } while (node.right != null){ if (node.right.getElement().equals(targetElement)){ result = true; break; } else { node = node.right; } } while (temp.left.getElement().equals(targetElement)){ if (temp.left.getElement().equals(targetElement)){ result = true; break; } else { temp = temp.left; } } return result; } public String toString() { UnorderedListADT<BinaryTreeNode<String>> nodes = new ArrayUnorderedList<BinaryTreeNode<String>>(); UnorderedListADT<Integer> levelList = new ArrayUnorderedList<Integer>(); BinaryTreeNode<String> current; String result = ""; int printDepth = this.getHeight(); int possibleNodes = (int)Math.pow(2, printDepth + 1); int countNodes = 0; nodes.addToRear((BinaryTreeNode<String>) root); Integer currentLevel = 0; Integer previousLevel = -1; levelList.addToRear(currentLevel); while (countNodes < possibleNodes) { countNodes = countNodes + 1; current = nodes.removeFirst(); currentLevel = levelList.removeFirst(); if (currentLevel > previousLevel) { result = result + "\n\n"; previousLevel = currentLevel; for (int j = 0; j < ((Math.pow(2, (printDepth - currentLevel))) - 1); j++) { result = result + " "; } } else { for (int i = 0; i < ((Math.pow(2, (printDepth - currentLevel + 1)) - 1)) ; i++) { result = result + " "; } } if (current != null) { result = result + (current.getElement()).toString(); nodes.addToRear(current.getLeft()); levelList.addToRear(currentLevel + 1); nodes.addToRear(current.getRight()); levelList.addToRear(currentLevel + 1); } else { nodes.addToRear(null); levelList.addToRear(currentLevel + 1); nodes.addToRear(null); levelList.addToRear(currentLevel + 1); result = result + " "; } } return result; } protected void preOrder(BinaryTreeNode<T> node, ArrayUnorderedList<T> tempList) { if (node != null){ tempList.addToRear(node.getElement()); preOrder(node.getLeft(),tempList); preOrder(node.getRight(),tempList); } } protected void postOrder(BinaryTreeNode<T> node, ArrayUnorderedList<T> tempList) { if (node != null){ postOrder(node.getLeft(),tempList); postOrder(node.getRight(),tempList); tempList.addToRear(node.getElement()); } } }
- 第二:利用中序和先序構建唯一的樹,關鍵程式碼如下:
public BinaryTreeNode initTree(String[] preOrder, int start1, int end1, String[] inOrder, int start2, int end2) {
if (start1 > end1 || start2 > end2) {
return null;
}
String rootData = preOrder[start1];
BinaryTreeNode head = new BinaryTreeNode(rootData);
//找到根節點所在位置
int rootIndex = findIndexInArray(inOrder, rootData, start2, end2);
//構建左子樹
BinaryTreeNode left = initTree(preOrder, start1 + 1, start1 + rootIndex - start2, inOrder, start2, rootIndex - 1);
//構建右子樹
BinaryTreeNode right = initTree(preOrder, start1 + rootIndex - start2 + 1, end1, inOrder, rootIndex + 1, end2);
head.left = left;
head.right = right;
return head;
}
}
第三:對於書上的背部疼痛診斷器簡單修改,無需放上。
第四:本次實驗唯一的難點,關鍵程式碼:
public static String toSuffix(String infix) {
String result = "";
String[] array = infix.split("\\s+");
Stack<LinkedBinaryTree> num = new Stack();
Stack<LinkedBinaryTree> op = new Stack();
for (int a = 0; a < array.length; a++) {
if (array[a].equals("+") || array[a].equals("-") || array[a].equals("*") || array[a].equals("/")) {
if (op.empty()) {
op.push(new LinkedBinaryTree<>(array[a]));
} else {
if ((op.peek().root.element).equals("+") || (op.peek().root.element).equals("-") && array[a].equals("*") || array[a].equals("/")) {
op.push(new LinkedBinaryTree(array[a]));
} else {
LinkedBinaryTree right = num.pop();
LinkedBinaryTree left = num.pop();
LinkedBinaryTree temp = new LinkedBinaryTree(op.pop().root.element, left, right);
num.push(temp);
op.push(new LinkedBinaryTree(array[a]));
}
}
} else {
num.push(new LinkedBinaryTree<>(array[a]));
}
}
while (!op.empty()) {
LinkedBinaryTree right = num.pop();
LinkedBinaryTree left = num.pop();
LinkedBinaryTree temp = new LinkedBinaryTree(op.pop().root.element, left, right);
num.push(temp);
}
Iterator itr=num.pop().iteratorPostOrder();
while (itr.hasNext()){
result+=itr.next()+" ";
}
return result;
}
- 第五:執行PP11.3之前的作業。
- 第六:對Java中的紅黑樹(TreeMap,HashMap)進行原始碼分析。
紅黑樹(TreeMap,HashMap)原始碼分析。
- 首先是對儲存結構進行分析,利用備註的形式在程式碼中標出。
static final class Entry<K,V> implements Map.Entry<K,V> {
K key; // 鍵
V value; // 值
Entry<K,V> left = null; // 左孩子
Entry<K,V> right = null; // 右孩子
Entry<K,V> parent; // 雙親節點
boolean color = BLACK; // 當前節點顏色
// 建構函式
Entry(K key, V value, Entry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
}- 之後是對
TreeMap的構造方法進行分析,TreeMap一共四個構造方法。
1.無引數構造方法
public TreeMap() {
comparator = null;
} 2.帶有比較器的構造方法
public TreeMap(Comparator<? super K> comparator) {
this.comparator = comparator;
} 3.帶Map的構造方法
public TreeMap(Map<? extends K, ? extends V> m) {
comparator = null;
putAll(m);
} 4.帶有SortedMap的構造方法
public TreeMap(SortedMap<K, ? extends V> m) {
comparator = m.comparator();
try {
buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
} - 對於第三個帶Map的構造方法,該方法不指定比較器,呼叫putAll方法將Map中的所有元素加入到TreeMap中。putAll的原始碼如下:
// 將map中的全部節點新增到TreeMap中
public void putAll(Map<? extends K, ? extends V> map) {
// 獲取map的大小
int mapSize = map.size();
// 如果TreeMap的大小是0,且map的大小不是0,且map是已排序的“key-value對”
if (size==0 && mapSize!=0 && map instanceof SortedMap) {
Comparator c = ((SortedMap)map).comparator();
// 如果TreeMap和map的比較器相等;
// 則將map的元素全部拷貝到TreeMap中,然後返回!
if (c == comparator || (c != null && c.equals(comparator))) {
++modCount;
try {
buildFromSorted(mapSize, map.entrySet().iterator(),
null, null);
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
return;
}
}
// 呼叫AbstractMap中的putAll();
// AbstractMap中的putAll()又會呼叫到TreeMap的put()
super.putAll(map);
} 顯然,如果Map裡的元素是排好序的,就呼叫buildFromSorted方法來拷貝Map中的元素,這在下一個構造方法中會重點提及,而如果Map中的元素不是排好序的,就呼叫AbstractMap的putAll(map)方法,該方法原始碼如下:
public void putAll(Map<? extends K, ? extends V> m) {
for (Map.Entry<? extends K, ? extends V> e : m.entrySet())
put(e.getKey(), e.getValue());
} put方法,同樣的,利用備註的形式在程式碼中標出。
public V put(K key, V value) {
Entry<K,V> t = root;
// 若紅黑樹為空,則插入根節點
if (t == null) {
// throw NullPointerException
// compare(key, key); // type check
root = new Entry<K,V>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
// 找出(key, value)在二叉排序樹中的插入位置。
// 紅黑樹是以key來進行排序的,所以這裡以key來進行查詢。
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
// 為(key-value)新建節點
Entry<K,V> e = new Entry<K,V>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
// 插入新的節點後,呼叫fixAfterInsertion調整紅黑樹。
fixAfterInsertion(e);
size++;
modCount++;
return null;
} - 刪除操作及對應
TreeMap的deleteEntry方法,deleteEntry方法同樣也只需按照二叉排序樹的操作步驟實現即可,刪除指定節點後,再對樹進行調整即可。deleteEntry方法的實現原始碼如下:
// 刪除“紅黑樹的節點p”
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
if (p.left != null && p.right != null) {
Entry<K,V> s = successor (p);
p.key = s.key;
p.value = s.value;
p = s;
}
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
p.left = p.right = p.parent = null;
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) {
root = null;
} else {
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
} 對於紅黑樹的原始碼分析到此就告一段落,因為最近時間有限,如果後期有空閒時間會繼續對其原始碼進行分析。
結果:
1.
2.
3.
4.
5.
3.實驗過程中遇到的問題和解決過程
- 問題1:在完成節點四的時候,以為只是簡單的將書上的表示式樹的程式碼改一改就好。
問題1解決方案:在寢室中跟王文彬同學討論相應問題的時候他提醒我說“雖然對於一棵表示式樹來說中序遍歷得到的就是中綴表示式,後序遍歷得到的就是後續表示式,但書上是利用字尾表示式構建了一棵樹,而我們的要求是利用中綴表示式構建一棵樹。”這讓我意識到了問題所在。好像問題沒有那麼簡單,事實也證明如此,的確沒有那麼簡單。
- 問題2:在做節點六時,從IDEA中打開了
TreeMap的原始碼,看到那3013行程式碼時,腦殼都大了一圈。 問題2解決方案:好在有於欣月同學的提醒,網上有類似的分析,所以在網上搜了一下相應的問題,發現果然有類似的原始碼分析,便去參考了一番。
其他(感悟、思考等)
感悟
- 學海無涯苦作舟。
