20172306 2018-2019-2 《程式設計與資料結構》實驗二報告

課程：《程式設計與資料結構》
班級： 1723
姓名： 劉辰
學號：20172306
實驗教師：王志強
實驗日期：2018年11月11日
必修/選修： 必修

1.實驗內容

• 實驗一：實現二叉樹
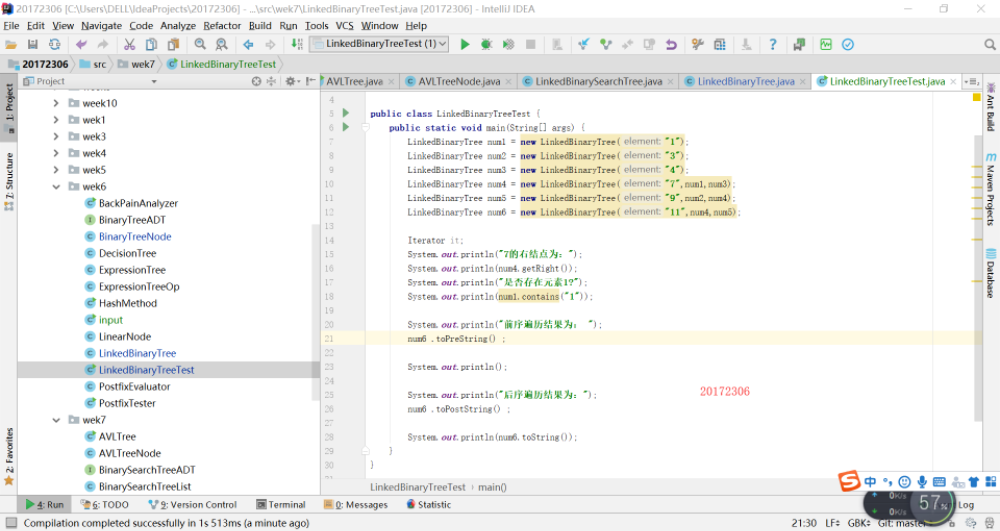
  參考教材p212,完成鏈樹LinkedBinaryTree的實現（getRight,contains,toString,preorder,postorder）
  用JUnit或自己編寫驅動類對自己實現的LinkedBinaryTree進行測試

• 實驗二：中序先序序列構造二叉樹
  基於LinkedBinaryTree，實現基於（中序，先序）序列構造唯一一棵二㕚樹的功能，比如給出中序HDIBEMJNAFCKGL和後序ABDHIEJMNCFGKL,構造出附圖中的樹
  用JUnit或自己編寫驅動類對自己實現的功能進行測試

• 實驗三：決策樹
  自己設計並實現一顆決策樹

• 實驗四：表示式樹
  輸入中綴表示式，使用樹將中綴表示式轉換為字尾表示式，並輸出字尾表示式和計算結果（如果沒有用樹，則為0分）

• 實驗五：二叉查詢樹
  完成PP11.3

• 實驗六：紅黑樹分析
  參考http://www.cnblogs.com/rocedu/p/7483915.html對Java中的紅黑樹（TreeMap，HashMap）進行原始碼分析，並在實驗報告中體現分析結果。
  （C:\Program Files\Java\jdk-11.0.1\lib\src\java.base\java\util）

2. 實驗過程及結果

實驗一：實現二叉樹的過程及結果

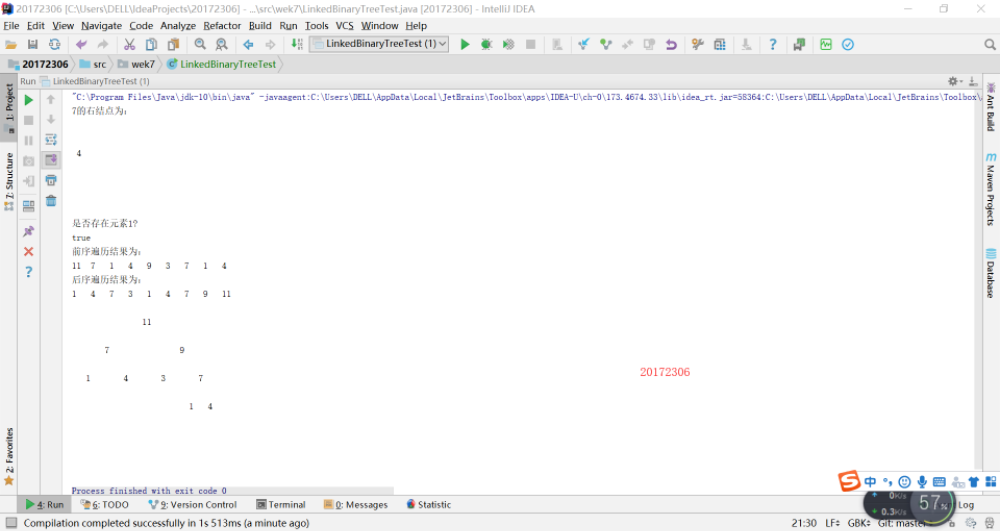
實驗二：中序先序序列構造二叉樹的過程及結果

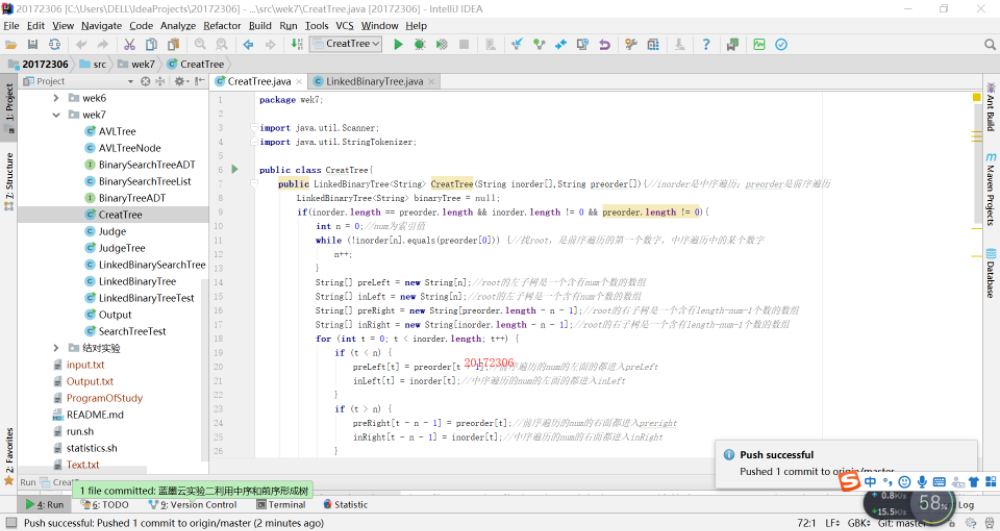
實驗三：決策樹的過程及結果

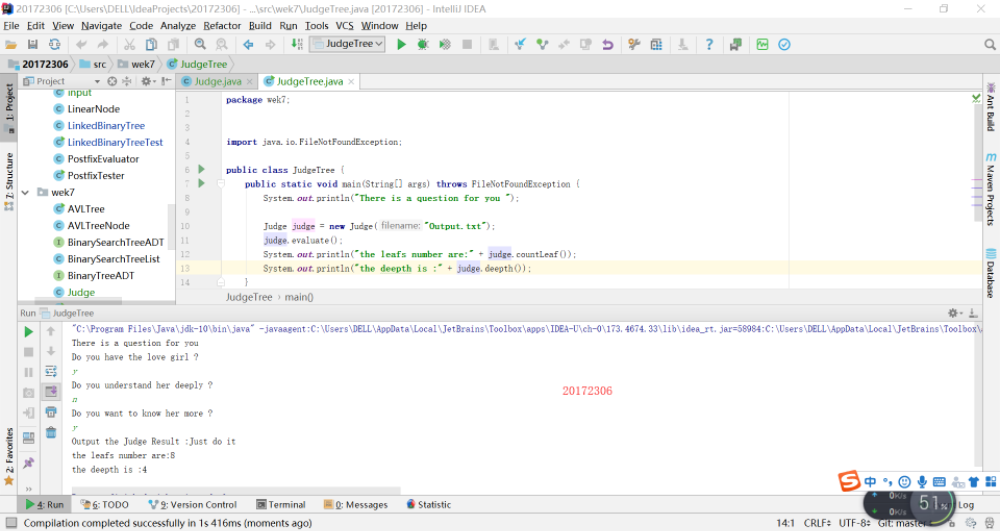
實驗四：表示式樹的過程及結果

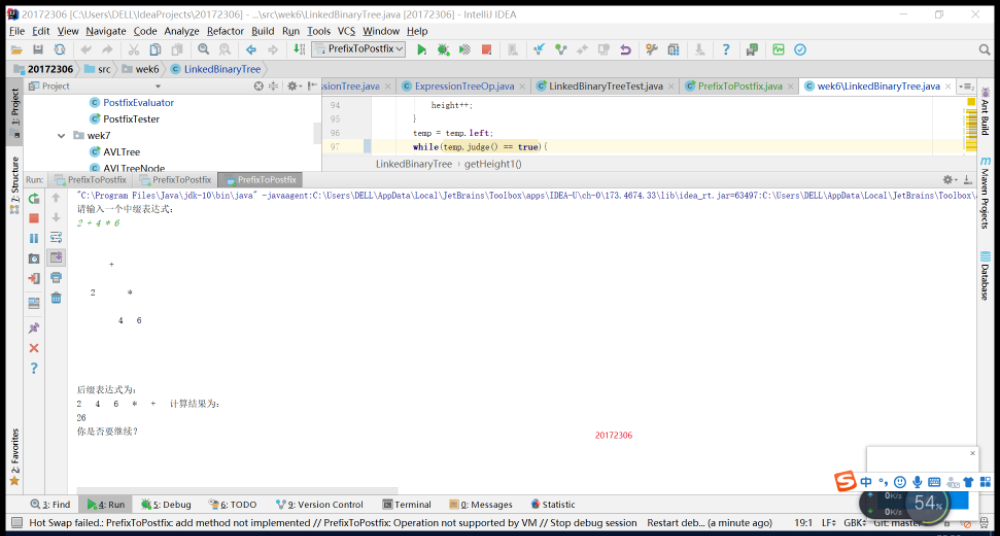
實驗五：二叉查詢樹

實驗六：紅黑樹分析（其實看了程式碼好長啊，但是很多都是註釋，註釋太長了）

• 先再瞭解一下紅黑樹的主要特點：
  • 每個節點都只能是紅色或者黑色
  • 根節點是黑色
  • 每個葉子節點是黑色的
  • 如果一個節點是紅色的，則它的兩個子節點都是黑色的
  • 從任意一個節點到每個葉子節點的所有路徑都包含相同數目的黑色節點
• TreeMap和HashMap的區別：
  • TreeMap的key是有序的，增刪改查操作的時間複雜度為O(log(n))，為了保證紅黑樹平衡，在必要時會進行旋轉，在TreeMap中用的是Comparator，Comparator一般表示類在某種場合下的特殊分類，需要定製化排序
• Comparator的介面

public interface Comparator<T> {
int compare(T o1, T o2);
boolean equals(Object obj);
 }

• HashMap的key是無序的，增刪改查操作的時間複雜度為O(1)，為了做到動態擴容，在必要時會進行resize。在HashMap中用的是Comparable，Comparable一般表示類的自然序
• Comparable介面

public interface Comparable<T> {
     public int compareTo(T o);
 }

• TreeMap
  • （1）put方法
    首先構造排序二叉樹，然後平衡二叉樹
    以根結點為初始節點遍歷；與當前結點進行比較，如果新增的結點值大，則以當前結點的右子結點作為新的當前結點。否則以當前結點的左子結點作為新的當前結點；迴圈遞迴上一步直到找到合適的葉子結點為止；將新增結點與上一步驟中找到的結點進行比對，如果新增結點較大，則新增為右子結點；否則新增為左子結點。
    按照上面步驟就可以將一個新增結點新增到排序二叉樹中合適的位置

  public V put(K key, V value) {
        Entry<K,V> t = root;
        if (t == null) {
        //如果根節點為null，將傳入的鍵值對構造成根節點（根節點沒有父節點，所以傳入的父節點為null）
            root = new Entry<K,V>(key, value, null);
            size = 1;
            modCount++;
            return null;
        }
        // 記錄比較結果
        int cmp;
        Entry<K,V> parent;
        // 分割比較器和可比較介面的處理
        Comparator<? super K> cpr = comparator;
        // 有比較器的處理
        if (cpr != null) {
            // do while實現在root為根節點移動尋找傳入鍵值對需要插入的位置
            do {
                // 記錄將要被摻入新的鍵值對將要節點(即新節點的父節點)
                parent = t;
                // 使用比較器比較父節點和插入鍵值對的key值的大小
                cmp = cpr.compare(key, t.key);
                // 插入的key較大
                if (cmp < 0)
                    t = t.left;
                // 插入的key較小
                else if (cmp > 0)
                    t = t.right;
                // key值相等，替換並返回t節點的value(put方法結束)
                else
                    return t.setValue(value);
            } while (t != null);
        }
        // 沒有比較器的處理
        else {
            // key為null丟擲NullPointerException異常
            if (key == null)
                throw new NullPointerException();
            Comparable<? super K> k = (Comparable<? super K>) key;
            // 與if中的do while類似，只是比較的方式不同
            do {
                parent = t;
                cmp = k.compareTo(t.key);
                if (cmp < 0)
                    t = t.left;
                else if (cmp > 0)
                    t = t.right;
                else
                    return t.setValue(value);
            } while (t != null);
        }
        // 沒有找到key相同的節點才會有下面的操作
        // 根據傳入的鍵值對和找到的“父節點”建立新節點
        Entry<K,V> e = new Entry<K,V>(key, value, parent);
        // 根據最後一次的判斷結果確認新節點是“父節點”的左孩子還是又孩子
        if (cmp < 0)
            parent.left = e;
        else
            parent.right = e;
        // 對加入新節點的樹進行調整
        fixAfterInsertion(e);
        // 記錄size和modCount
        size++;
        modCount++;
        // 因為是插入新節點，所以返回的是null
        return null;
    }

  在put(K key,V value)方法的末尾呼叫了fixAfterInsertion(Entry<K,V> x)方法，這個方法負責在插入結點後調整樹結構和著色，以滿足紅黑樹的要求。

private void fixAfterInsertion(Entry<K,V> x) {
    // 插入節點預設為紅色
    x.color = RED;
    // 迴圈條件是x不為空、不是根節點、父節點的顏色是紅色（如果父節點不是紅色，則沒有連續的紅色節點，不再調整）
    while (x != null && x != root && x.parent.color == RED) {
        // x節點的父節點p（記作p）是其父節點pp（p的父節點，記作pp）的左孩子（pp的左孩子）
        if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
            // 獲取pp節點的右孩子r
            Entry<K,V> y = rightOf(parentOf(parentOf(x)));
            // pp右孩子的顏色是紅色（colorOf(Entry e)方法在e為空時返回BLACK），不需要進行旋轉操作（因為紅黑樹不是嚴格的平衡二叉樹）
            if (colorOf(y) == RED) {
                // 將父節點設定為黑色
                setColor(parentOf(x), BLACK);
                // y節點，即r設定成黑色
                setColor(y, BLACK);
                // pp節點設定成紅色
                setColor(parentOf(parentOf(x)), RED);
                // x“移動”到pp節點
                x = parentOf(parentOf(x));
            } else {//父親的兄弟是黑色的，這時需要進行旋轉操作，根據是“內部”還是“外部”的情況決定是雙旋轉還是單旋轉
                // x節點是父節點的右孩子（因為上面已近確認p是pp的左孩子，所以這是一個“內部，左-右”插入的情況，需要進行雙旋轉處理）
                if (x == rightOf(parentOf(x))) {
                    // x移動到它的父節點
                    x = parentOf(x);
                    // 左旋操作
                    rotateLeft(x);
                }
                // x的父節點設定成黑色
                setColor(parentOf(x), BLACK);
                // x的父節點的父節點設定成紅色
                setColor(parentOf(parentOf(x)), RED);
                // 右旋操作
                rotateRight(parentOf(parentOf(x)));
            }
        } else {
            // 獲取x的父節點（記作p）的父節點（記作pp）的左孩子
            Entry<K,V> y = leftOf(parentOf(parentOf(x)));
            // y節點是紅色的
            if (colorOf(y) == RED) {
                // x的父節點，即p節點，設定成黑色
                setColor(parentOf(x), BLACK);
                // y節點設定成黑色
                setColor(y, BLACK);
                // pp節點設定成紅色
                setColor(parentOf(parentOf(x)), RED);
                // x移動到pp節點
                x = parentOf(parentOf(x));
            } else {
                // x是父節點的左孩子（因為上面已近確認p是pp的右孩子，所以這是一個“內部，右-左”插入的情況，需要進行雙旋轉處理），
                if (x == leftOf(parentOf(x))) {
                    // x移動到父節點
                    x = parentOf(x);
                    // 右旋操作
                    rotateRight(x);
                }
                // x的父節點設定成黑色
                setColor(parentOf(x), BLACK);
                // x的父節點的父節點設定成紅色
                setColor(parentOf(parentOf(x)), RED);
                // 左旋操作
                rotateLeft(parentOf(parentOf(x)));
            }
        }
    }
    // 根節點為黑色
    root.color = BLACK;
}

在這個裡面在平衡二叉樹時，還有涉及左旋和右旋的操作。

• （2）get方法

 public V get(Object key) {
    Entry<K,V> p = getEntry(key);
    return (p==null ? null : p.value);
 }

在這個get方法中涉及了getEntry的方法，這個主要是來尋找結點的

final Entry<K,V> getEntry(Object key) {
    // 如果有比較器，返回getEntryUsingComparator(Object key)的結果
    if (comparator != null)
        return getEntryUsingComparator(key);
    // 查詢的key為null，丟擲NullPointerException
    if (key == null)
        throw new NullPointerException();
    // 如果沒有比較器，而是實現了可比較介面
    Comparable<? super K> k = (Comparable<? super K>) key;
    // 獲取根節點
    Entry<K,V> p = root;
    // 對樹進行遍歷查詢節點
    while (p != null) {
        // 把key和當前節點的key進行比較
        int cmp = k.compareTo(p.key);
        // key小於當前節點的key
        if (cmp < 0)
            // p “移動”到左節點上
            p = p.left;
        // key大於當前節點的key
        else if (cmp > 0)
            // p “移動”到右節點上
p = p.right;
        // key值相等則當前節點就是要找的節點
        else
            // 返回找到的節點
            return p;
        }
    // 沒找到則返回null
    return null;
}

• （3）remove方法
  真正實現刪除結點的是deleteEntry的方法

private void deleteEntry(Entry<K,V> p) {
// 記錄樹結構的修改次數
modCount++;
// 記錄樹中節點的個數
    size--;

// p有左右兩個孩子的情況  標記①
if (p.left != null && p.right != null) {
        // 獲取繼承者節點（有兩個孩子的情況下，繼承者肯定是右孩子或右孩子的最左子孫）
        Entry<K,V> s = successor (p);
        // 使用繼承者s替換要被刪除的節點p，將繼承者的key和value複製到p節點，之後將p指向繼承者
        p.key = s.key;
        p.value = s.value;
        p = s;
    } 

// Start fixup at replacement node, if it exists.
// 開始修復被移除節點處的樹結構
// 如果p有左孩子，取左孩子，否則取右孩子    標記②
    Entry<K,V> replacement = (p.left != null ? p.left : p.right);
    if (replacement != null) {
        // Link replacement to parent
        replacement.parent = p.parent;
        // p節點沒有父節點，即p節點是根節點
        if (p.parent == null)
            // 將根節點替換為replacement節點
            root = replacement;
        // p是其父節點的左孩子
        else if (p == p.parent.left)
            // 將p的父節點的left引用指向replacement
            // 這步操作實現了刪除p的父節點到p節點的引用
            p.parent.left  = replacement;
        else
            // 如果p是其父節點的右孩子，將父節點的right引用指向replacement
            p.parent.right = replacement;
        // 解除p節點到其左右孩子和父節點的引用
        p.left = p.right = p.parent = null;
        if (p.color == BLACK)
            // 在刪除節點後修復紅黑樹的顏色分配
            fixAfterDeletion(replacement);
} else if (p.parent == null) { 
/* 進入這塊程式碼則說明p節點就是根節點（這塊比較難理解，如果標記①處p有左右孩子，則找到的繼承節點s是p的一個祖先節點或右孩子或右孩子的最左子孫節點，他們要麼有孩子節點，要麼有父節點，所以如果進入這塊程式碼，則說明標記①除的p節點沒有左右兩個孩子。沒有左右孩子，則有沒有孩子、有一個右孩子、有一個左孩子三種情況，三種情況中只有沒有孩子的情況會使標記②的if判斷不通過，所以p節點只能是沒有孩子，加上這裡的判斷，p沒有父節點，所以p是一個獨立節點，也是樹種的唯一節點……有點難理解，只能解釋到這裡了，讀者只能結合註釋慢慢體會了），所以將根節點設定為null即實現了對該節點的刪除 */
        root = null;
} else { /* 標記②的if判斷沒有通過說明被刪除節點沒有孩子，或它有兩個孩子但它的繼承者沒有孩子。如果是被刪除節點沒有孩子，說明p是個葉子節點，則不需要找繼承者，直接刪除該節點。如果是有兩個孩子，那麼繼承者肯定是右孩子或右孩子的最左子孫 */
        if (p.color == BLACK)
            // 調整樹結構
            fixAfterDeletion(p);
        // 這個判斷也一定會通過，因為p.parent如果不是null則在上面的else if塊中已經被處理
        if (p.parent != null) {
            // p是一個左孩子
            if (p == p.parent.left)
                // 刪除父節點對p的引用
                p.parent.left = null;
            else if (p == p.parent.right)// p是一個右孩子
                // 刪除父節點對p的引用
                p.parent.right = null;
            // 刪除p節點對父節點的引用
            p.parent = null;
        }
    }
}

• HashMap
  • HashMap的構造方法

//1.構造一個帶指定初始容量和載入因子的空HashMap
    public HashMap(int initialCapacity, float loadFactor) {
        if (initialCapacity < 0)
            throw new IllegalArgumentException("Illegal initial capacity: " +
                                               initialCapacity);
        if (initialCapacity > MAXIMUM_CAPACITY)
            initialCapacity = MAXIMUM_CAPACITY;
        if (loadFactor <= 0 || Float.isNaN(loadFactor))
            throw new IllegalArgumentException("Illegal load factor: " +
                                               loadFactor);
        this.loadFactor = loadFactor;
        this.threshold = tableSizeFor(initialCapacity);
    }
    //2.構造一個帶指定初始容量和預設載入因子(0.75)的空 HashMap
    public HashMap(int initialCapacity)
    {
        this(initialCapacity, DEFAULT_LOAD_FACTOR);
    }
     //3.構造一個具有預設初始容量 (16)和預設載入因子 (0.75)的空 HashMap
    public HashMap() 
    {
        this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
    }
     //4.構造一個對映關係與指定 Map相同的新 HashMap
    public HashMap(Map<? extends K, ? extends V> m)
    {
        this.loadFactor = DEFAULT_LOAD_FACTOR;
        putMapEntries(m, false);
    }

• （1）put方法

public V put(K key, V value)
    {
        return putVal(hash(key), key, value, false, true);
    }
    final V putVal(int hash, K key, V value, boolean onlyIfAbsent,boolean evict) 
    {
        Node<K,V>[] tab; Node<K,V> p; int n, i;
        if ((tab = table) == null || (n = tab.length) == 0)
            n = (tab = resize()).length;
        if ((p = tab[i = (n - 1) & hash]) == null)//該key的hash值對應的那個節點為空
            tab[i] = newNode(hash, key, value, null);//新建節點
        else
        {
            //節點不為空，先比較連結串列上的第一個節點
            Node<K,V> e; K k;
            if (p.hash == hash &&((k = p.key) == key || (key != null && key.equals(k))))
                e = p;
            else if (p instanceof TreeNode)
                e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
            else {
                for (int binCount = 0; ; ++binCount) 
                {
                    if ((e = p.next) == null) {
                        p.next = newNode(hash, key, value, null);
                        if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                            treeifyBin(tab, hash);
                        break;
                    }
                    if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                        break;
                    p = e;
                }
            }
            if (e != null)  //若該key對應的鍵值對已經存在，則用新的value取代舊的value
            {
                V oldValue = e.value;
                if (!onlyIfAbsent || oldValue == null)
                    e.value = value;
                afterNodeAccess(e);
                return oldValue;
            }
        }
       // 若“該key”對應的鍵值對不存在，則將“key-value”新增到table中 
        ++modCount;
        //如果加入該鍵值對後超過最大閥值，則進行resize操作
        if (++size > threshold)
            resize();
        afterNodeInsertion(evict);
        return null;
    }

• （2）get方法

public V get(Object key) {
        Node<K,V> e;
        //傳入key的hash
        return (e = getNode(hash(key), key)) == null ? null : e.value;
    }

    final Node<K,V> getNode(int hash, Object key) {
        Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
        //這裡訪問(n - 1) & hash其實就是jdk1.7中indexFor方法的作用
        if ((tab = table) != null && (n = tab.length) > 0 &&
            (first = tab[(n - 1) & hash]) != null) {
            //判斷桶索引位置的節點是不是相同（通過hash和equals判斷），如果相同返回此節點
            if (first.hash == hash && // always check first node
                ((k = first.key) == key || (key != null && key.equals(k))))
                return first;
            if ((e = first.next) != null) {
                //判斷是否是紅黑樹節點，如果是查詢紅黑樹
                if (first instanceof TreeNode)
                    return ((TreeNode<K,V>)first).getTreeNode(hash, key);
                do {
                    //如果是連結串列，遍歷連結串列
                    if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                        return e;
                } while ((e = e.next) != null);
            }
        }
        //如果不存在返回null
        return null;
    }

3. 實驗過程中遇到的問題和解決過程

• 問題1：實驗三的那個決策樹，我最開始完全不知道要幹嘛，後面的數字我也有點懵

• 問題1解決方案：我進行了幾次實驗，重複的利用Y、N來看看都對應什麼，後來發現，後面的數字其實就是將之前的各個句子當做數字，然後一個個形成樹，後來我試圖再新增一個樹，我就新增到了那串數字的最後，但是會有問題，有時會出現BUG

• 問題1後續解決方案：後來我在想，是不是那個數字是有規律的，我就繼續找，後來才知道，其實順序是從樹的左下到右下，再向上到頭的

• 問題2：在做實驗四的時候，我最開始的toString我用的是利用我之前的LinkedBinaryTree的後序的迭代器進行編寫的，但是總是出現這樣的問題，它出現的不是後序的輸出
  

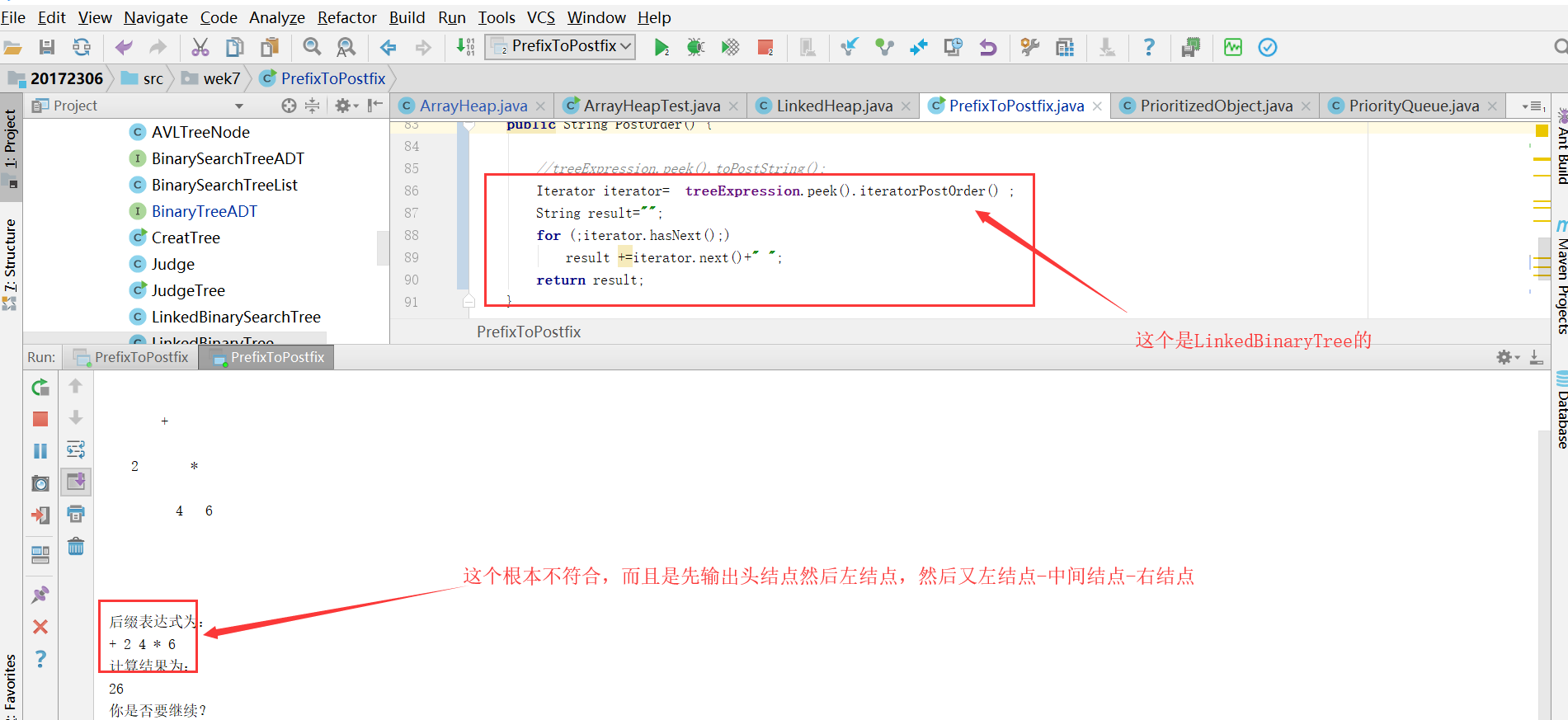
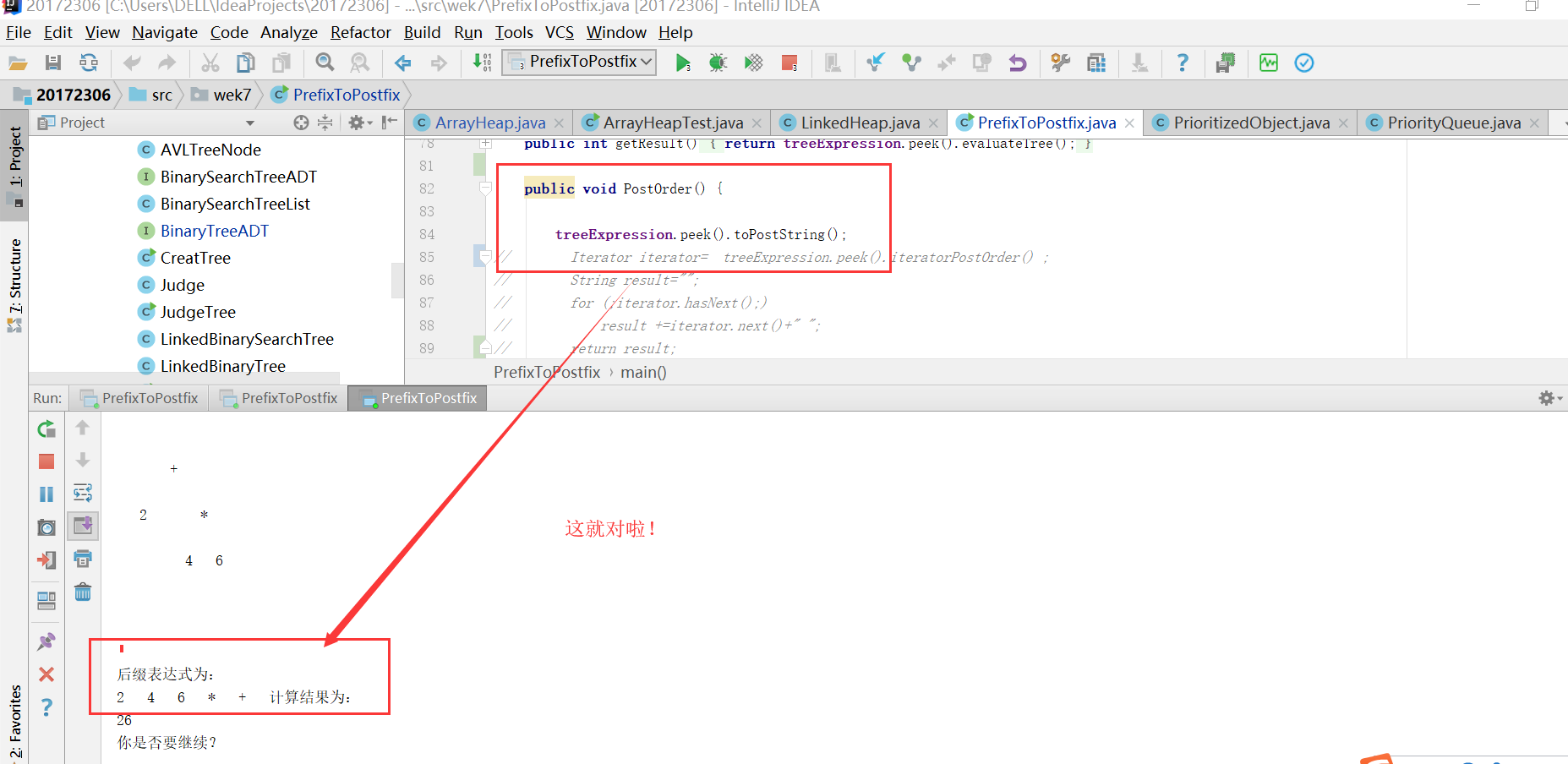
• 問題2解決方案：我一開始以為是不是我的LinkedBinaryTree的那段程式碼有問題，我想到之前測試過，我就又測試一遍，發現是沒問題的；之後，我試圖看其他人關於LinkedBinaryTree的程式碼，發現跟我的一樣啊，因為這個其實每個人都是基本一樣的；我後來又想，是不是不是我的toString有問題呢，我就單步除錯了一下，發現就是這個問題；我最後嘗試將IDEA關掉重進，結果亦如此，主要是我跟別人的一樣啊問題出在哪呢？？我很疑惑，而且依舊疑惑，問了仇夏和結對夥伴，依舊沒有結果。後來我換了一個toString，我呼叫了toPostring方法，是我LinkedBinaryTree的輸出後序的方法，結果就成功了。
  

• 問題3：其實最開始做中序先序表達樹的時候吧，我有點蒙圈，我不知道怎麼做

• 問題3解決方案：很幸運，譚鑫不厭其煩，我問他，他就給我講了，其實就是先序的第一個為root，然後在中序中找root，把它分成兩部分，再在這兩部分中的先序繼續找小樹中的root，在中序中繼續分兩部分，以此向下。主要總結就是：先序是來找root，中序是來分塊的。然後其實程式碼就很好寫啦！

其他（感悟、思考等）

我覺得實驗三的那個決策樹，特別好玩，我可以用這個來測試我想測試的東西，還挺好玩的，頭回覺得會Java是一件很好的事情，如果我不會樹的話，我就沒法把問題弄出來了；實驗四我覺得特別難，其實都是在理解其他人的程式碼的情況下漸漸寫出來的；實驗六嘛，嗯~我覺得那個紅黑樹的原始碼實在很長，很難懂，很難，很難懂！！！