機器學習課程中做的一些實驗題目，拿來和大家分享一下。

實驗步驟與內容：

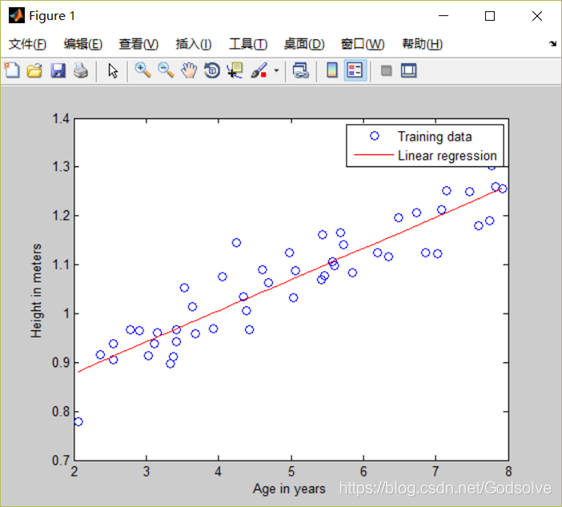
1. 載入資料集並繪製散點圖
   MATLAB中載入資料集的方法是“load”函式，繪製散點圖的方法是“plot”函式，並且還可以使用“label”函式來為座標軸做標註。
   得出結果如圖：
   

2. 在梯度下降之前，要使用x = [ones(m, 1) x]語句來給資料集x加上一列，訓練資料中的年齡值實際上位於x的第二列。
   此時的線性迴歸模型為
   
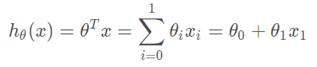
   使用實驗檔案中給出的學習率，來初始化引數theta=0(i.e.,θ0=θ1=0)，並從該初始起點開始一次梯度下降迭代。 記錄第一次迭代後得到的 theta0和theta1的值。
   在程式中體現為：theta = zeros(size(x(1,:)))’;

3. 線性迴歸模型為

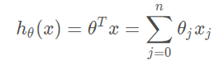
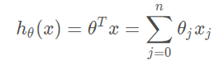
梯度下降演算法的更新規則為

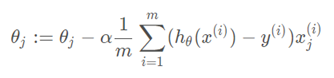
而這兩個函式在程式中，可以將更新規則中的h（x）替換為theta*x

然後迴圈1500次，得到一元線性迴歸方程，結果為

三歲半的孩子身高約0.9737米，七歲的孩子身高約為1.1973米
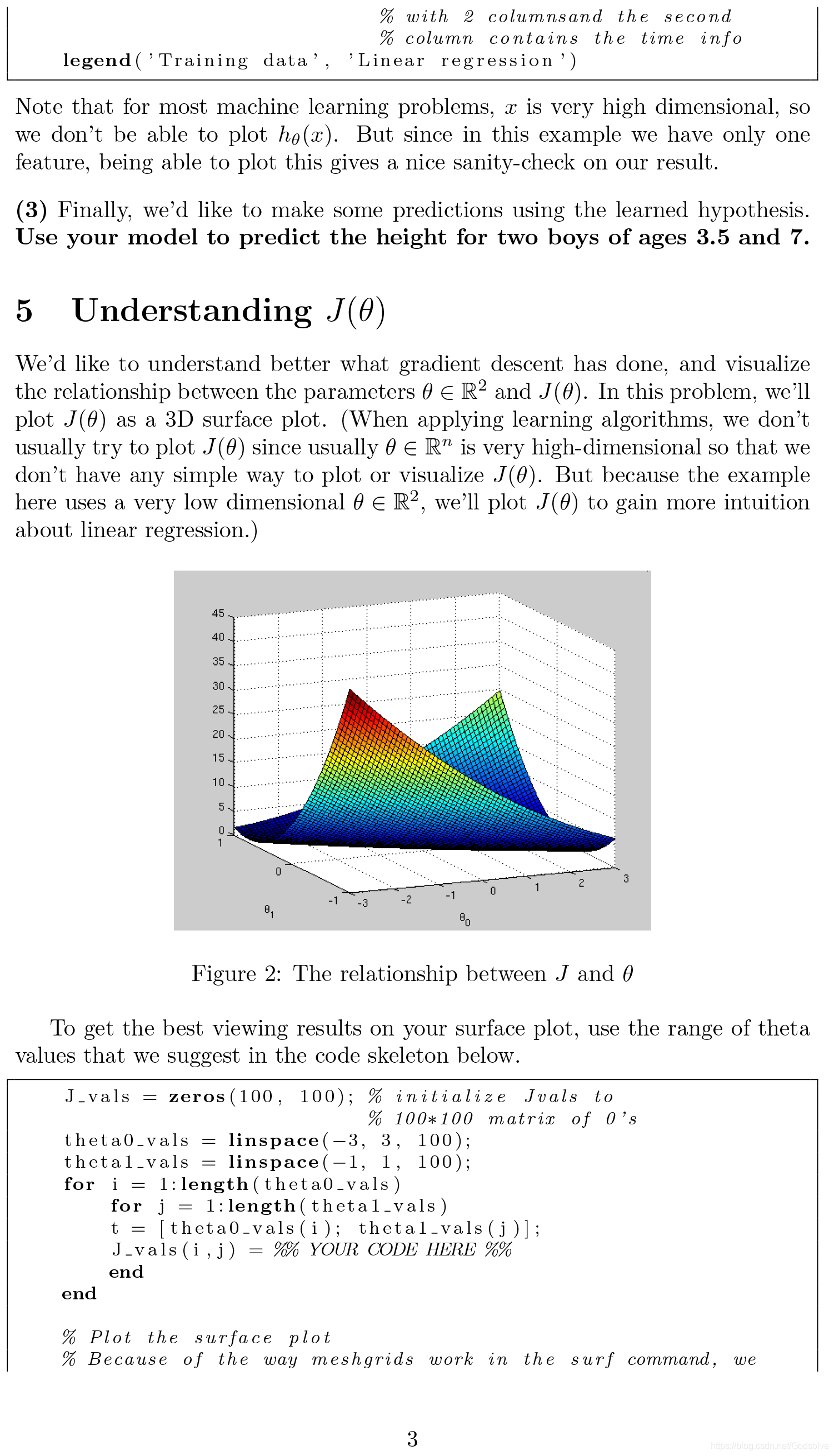
4. 對J（θ）的理解
視覺化引數θ來幫助理解梯度下降函式，繪製出J（θ）的3D表面圖。

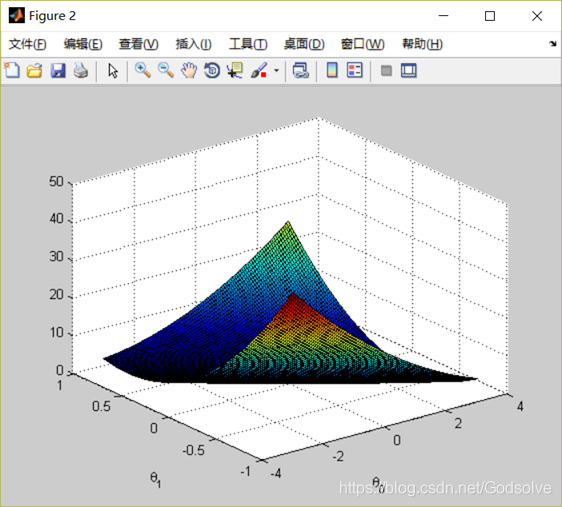
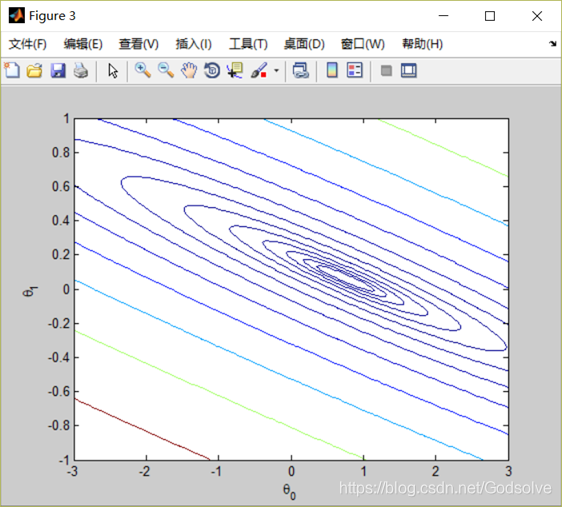
程式碼自取：

clear all; close all; clc
x = load('ex1x.dat'); y = load('ex1y.dat');
m = length(y); 
figure; 
plot(x, y, 'o');
ylabel('Height in meters')
xlabel('Age in years')

% Gradient descent
x = [ones(m, 1) x]; 
theta = zeros(size(x(1,:)))'; 
MAX_ITR = 1500;
alpha = 0.07;

for num_iterations = 1:MAX_ITR
 
  
   % Here is the gradient
   grad = (1/m).* x' * ((x * theta) - y);
   
   % Here is the actual update
   theta = theta - alpha .* grad;
   
   
end
theta;
hold on; 
plot(x(:,2), x*theta, 'r-');
legend('Training data', 'Linear regression')
hold off 

exact_theta = (x' * x)\x' * y

% Predict values for age 3.5 and 7
predict1 = [1, 3.5] *theta
predict2 = [1, 7] * theta
theta0_vals = linspace(-3, 3, 100);
theta1_vals = linspace(-1, 1, 100);

% initialize J_vals to a matrix of 0's
J_vals = zeros(length(theta0_vals), length(theta1_vals));

for i = 1:length(theta0_vals)
     for j = 1:length(theta1_vals)
     t = [theta0_vals(i); theta1_vals(j)];    
     J_vals(i,j) = (0.5/m) .* (x * t - y)' * (x * t - y);
   end
end

J_vals = J_vals';
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('\theta_0'); ylabel('\theta_1');

figure;
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 2, 15))
xlabel('\theta_0'); ylabel('\theta_1');