主要的思路就是將這個題目轉換一下去求。題目上面說，雷達只會在x軸上面，那麼我們就可以去算一下大致的幾種情況：

第一種，雷達全面覆蓋的到。那麼轉換一下思路。

第二種，存在幾個特殊的，比較高的位置，雷達無法覆蓋，就是雷達最高為m，但是他的位置高度超過了m，所以直接輸出-1.

思路就是我們可以把每一個點轉換一下，看成一個圓，去思考一下。如果點可以被覆蓋的到，那麼圓與x軸就會相交或者相切，以半徑為雷達m範圍的圓。如果他們不相交，那麼就是說雷達掃描不到，因為雷達只在x軸上面。

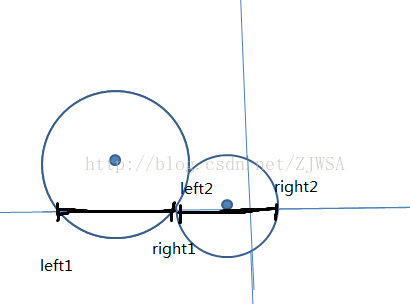
如圖：

在這裡我們看見了因為相交的部分不重合，所以要想在x軸上面安雷達覆蓋這兩個點，我們至少需要兩個。

如圖的思想，我們再加一個點所構成的圓。在此註明一點就是，在x軸上面的範圍就是表明雷達如果要覆蓋這點，那麼他就必須在這個範圍裡面。因為二點，一必須在x軸上面，二他是以雷達範圍的圓，不在就說明點與雷達的範圍超過了雷達掃描的範圍。

在此圖，我們可以更好的看出如果，範圍重合了，就說明他們可以用一個雷達去掃描得到。

最後得到的其實就是這個圖了，求的就是公共覆蓋的就用一點，不是公共覆蓋的就開闢，把一個範圍不斷的縮小，縮小的區域就是共同的雷達，不在縮小的區域類，就代表著，存在一點和你不含有公共區域。

所以題目的思路就清晰了，先把點轉化為在x軸上面的範圍，求範圍的話，根據數學的公式就可以求出來了。[x-根號下(r*r-y*y)，x+根號下(r*r-y*y)]，這個範圍就可以了。最後題目就轉換成了求公共覆蓋範圍用一個雷達，不在就新建一個雷達。

既然我要用一個圓嘗試著（雷達範圍，半徑為r）去覆蓋島嶼，那為何不以島嶼為圓心r為半徑畫一個圓（記為圓O），於是只要雷達在這個圓裡那麼這個島嶼就能被覆蓋。而從前面的分析可知，雷達必然要佈置在x軸上，所以雷達肯定放在圓O與x軸的那段交線區間上，如圖：

所以我們可以將所有的島嶼對應的這段區間記錄下來，然後以區間左界從小到大排序就行，之後從第一個區間開始，如果第二個區間與其有交集，就更新這個交集，並從佇列中除去區間1，2，如果第三個區間與這個交集又有交集，那麼便更新交集併除去區間3直到不滿足有交集為止。然後繼續模擬這個過程就行了，每模擬以此這個過程ANS++（即區間選點問題）
 

但是這道題注意浮點誤差！以及sqrt（double）的使用

#include<cmath>
#include<cstdio>
#include<algorithm>
#include<iostream>
#define MAXN 1010
using namespace std;
struct node 
{
	double xl;//最左可被偵測座標
	double xr;//最右可被偵測座標
}island[MAXN];
int n,d,x,y,cnt,flag;
double offset;
 
bool cmp(node a,node b)
{
	return a.xl<b.xl;
}
 
int find()
{
	int num=0;
	double cur; 	//當前最右可被偵測座標 
	cur=island[1].xr;
	num++;
	for(int i=2;i<=n;i++)
	{
		if(island[i].xl-cur>1e-6) //下個島嶼的最左座標大於當前最右可被偵測座標 
		{
			num++;
			cur=island[i].xr;
		}
		else
			if(island[i].xr-cur<1e-6) //下個島嶼的最右座標小於當前最右可被偵測座標 
			    cur=island[i].xr;
	}
	return num; 
}
 
int main()
{
    while(~scanf("%d %d",&n,&d))
    {
    	if(n==0&&d==0)break;
        flag=0;
        cnt++;
        for(int i=1;i<=n;i++)
        {
            scanf("%d %d",&x,&y);
            if(y>d)	flag=1;
            
            offset=sqrt((double)(d*d-y*y));
            
            island[i].xl=x-offset;
            island[i].xr=x+offset;
        }
        if(flag)
        {
            printf("Case %d: -1\n",cnt);
            continue;
        }
        sort(island+1,island+n+1,cmp);
        int ans=find();
        printf("Case %d: %d\n",cnt,ans);
    }
    return 0;
}