[OpenGL] 紋理高階篇 - 法線貼圖
概念引入
對於三維渲染中的物體而言,出色的光影渲染往往能夠給畫面帶來質的飛躍提升。由光照方程可見,物體表面的法線對於最終的光照計算結果起著重要的作用,而物體的表面的頂點/面數則對光照沒有太大的影響——這為我們的一個想法提供了可能性,也就是說,我們可不可以通過高模來獲取法線,然後用低模渲染物體,並把高模的法線應用到物體上。此時,經過光照計算,呈現在我們眼前的就是高模下的光照細節表現,讓我們感覺模型似乎很精細。
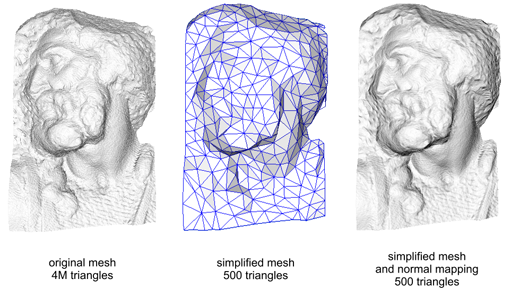
(圖片來自網路)
基於這個想法,法線貼圖誕生了。我們把法線存在一張圖片裡,通過紋理對映建立法線和畫素的對應關係,就能基本還原高模的法線分佈。比起高模,法線貼圖能夠在畫面效果不打折扣的條件下,大大減少記憶體視訊記憶體的佔用量,並提高渲染效率。
以下是不使用法線貼圖,使用頂點法線進行渲染的結果:

以下是使用法線貼圖進行渲染的結果:

將鏡頭拉近,我們可以觀察到豐富的表面細節:

法線的儲存與讀取
法線是一個向量,經過歸一化計算後,分佈在[-1,1]之間,為了把它壓縮到[0,1]之內,需要做一個簡單的線性對映:
color = (N + 1) / 2
那麼類似的,從法線貼圖中解析法線的時候,要做一個逆運算:
N = 2 * color - 1
但是,對於解析後得到的法線,我們仍然不能直接使用它,因為出於一種不成文的規矩,我們的法線貼圖中的法線並不是記錄在世界座標系下的,而是儲存在一個特殊的座標系下,即切線空間中。
切線空間是什麼?對於一個網格模型,我們逐頂點來分析,每個頂點都有著自己的切線空間,如下圖所示,我們可以將其稱為TBN空間。其中N代表該點處的法線,T(tangent)和B(binormal)都是該點處的切線。由於一個點處的切線有無數條,我們指定T切線是沿著紋理的u座標方向的,B切線是沿著紋理的v座標方向的。

那麼,對於法線紋理中的法線,它是在TBN空間儲存的,具體可能是下圖的樣子。由圖可見圖中有兩個法線(N),一個是黑色的N,另一個是藍色的N',要注意區分這兩者。前者是實際使用的模型中,垂直於當前點的那個法線(點法線),而後者是從法線紋理中讀取的法線(畫素法線),也就是說,讀取的法線不總是垂直於點,而是在原法線的基礎上有一點偏移。
在法線貼圖中,我們使用切線空間來儲存,這也就意味著我們可以很容易從其推匯出法線的偏移資訊,而這個偏移資訊是和具體的模型無關的,也就是說,當我們使用切線空間下的法線貼圖時,我們可以將一張貼圖應用於不同模型上,無論是球形,圓柱體或是正方體,甚至是更為複雜的模型。

計算TBN矩陣
也許上面的解析不一定能夠完全理解,那麼可以試著一起動手計算一遍TBN矩陣,來更好地認識前文提及的一些概念。
也就是說,我們需要在給出模型按照三角形排布的點集時,自動計算出它的法線以及兩條切線。此時,我們的輸入是網格中三角形三個點的模型空間座標,以及uv紋理座標。
(1) 計算面法線
在已知三個點座標的情況下,面法線的計算非常簡單,只需要求三角形中兩個向量的叉積即可。在這個計算過程中,我們可能需要考慮到的一個問題是,垂直於一個面片的法線有兩個方向,我們需要保證我們求出的法線是實際我們需要的那個方向的法線。
在OpenGL中,對於組成三角形的三個點對應的法線方向有著這麼一個規定,根據輸入的三個點的方向,按照右手定則,讓四指方向指向三個點的流動方向,大拇指的朝向即為法線方向。所以在計演算法線時,我們也需要按照這一規律進行計算。
(2) 計算面切線
由於第二條切線可以通過叉乘得到,在這裡我們只計算切線T。由於切線T取得沿著紋理座標u方向,所以我們實際上需要計算向量u。

如上圖,向量e0和e1可以用模型空間下的座標來表示,即:
e0 = vertex1.position - vetex0.position
e1 = vertex2.position - vertex0.position
也可以使用TBN空間作為基向量來表示:
e0 = t1 * T + b1 * B
e1 = t2 * T + b2 * B
其中,t1,t2,b1,b2是向量之間的u,v差值。
聯立以上方程組,可以求解出T,B兩個向量。我們最終保留切線T的計算結果。
(3) 將面法/切線轉換到點法/切線
由於我們的計算是基於面來計算的,所以我們得到的實際上是面法線和麵切線。但是,我們傳入頂點著色器中,應該為頂點法線和頂點切線。此處我們還需要經過一次處理,即對於每個點,求其鄰接面的面法線/切線的平均值。
我們最終計算的程式碼如下:
struct VertexData
{
QVector3D position;
QVector3D tangent;
QVector3D normal;
QVector2D texture; // texcoord
int adjoinPlane = 0;
};
void CalNormalAndTangent(VertexData& vertex0, VertexData& vertex1, VertexData& vertex2)
{
float u0 = vertex0.texture.x();
float v0 = vertex0.texture.y();
float u1 = vertex1.texture.x();
float v1 = vertex1.texture.y();
float u2 = vertex2.texture.x();
float v2 = vertex2.texture.y();
float t1 = u1 - u0;
float b1 = v1 - v0;
float t2 = u2 - u0;
float b2 = v2 - v0;
QVector3D e0 = vertex1.position - vertex0.position;
QVector3D e1 = vertex2.position - vertex0.position;
float k = t1 * b2 - b1 * t2;
QVector3D tangent;
tangent = k * QVector3D(b2 * e0.x() - b1 * e1.x(),b2 * e0.y() - b1 * e1.y(),b2 * e0.z() - b1 * e1.z());
QVector3D normal;
normal = QVector3D::crossProduct(e0, e1);
QVector<VertexData*> vertexArr = { &vertex0, &vertex1, &vertex2};
for(int i = 0;i < vertexArr.size();i++)
{
vertexArr[i]->adjoinPlane++;
float ratio = 1.0f / vertexArr[i]->adjoinPlane;
vertexArr[i]->normal = vertexArr[i]->normal * (1 - ratio) + normal * ratio;
vertexArr[i]->tangent = vertexArr[i]->tangent * (1 - ratio) + tangent * ratio;
}
}
將法線貼圖從切線空間轉換到世界空間
為了能夠應用法線的計算,我們需要統一計算的座標空間,我們有兩個選擇,一個是在切線空間下進行光照的計算,這意味著我們要把光照方向等向量轉換到切線空間,另一個是在世界空間上進行光照計算,這意味著我們要把法線轉換到世界座標系。但無論怎樣,我們都需要TBN矩陣參與座標空間的轉換運算。
在此我們介紹將法線從切線空間轉換到世界空間的方法。
(1) 頂點著色器
在這裡,我們所做的事情包括像往常一樣的把頂點座標轉換到投影空間,並記錄頂點的世界座標,將世界座標、紋理座標、法線和切線傳遞到片元著色器。需要注意的是,我們之前求得的法線和切線都是模型座標系下的,我們也同樣要將它們轉換到世界座標系進行計算。
uniform mat4 ModelMatrix;
uniform mat4 IT_ModelMatrix;
uniform mat4 ViewMatrix;
uniform mat4 ProjectMatrix;
attribute vec4 a_position;
attribute vec3 a_normal;
attribute vec3 a_tangent;
attribute vec2 a_texcoord;
varying vec2 v_texcoord;
varying vec3 v_tangent;
varying vec3 v_normal;
varying vec3 worldPos;
void main()
{
gl_Position = ModelMatrix * a_position;
worldPos = vec3(gl_Position);
gl_Position = ViewMatrix * gl_Position;
gl_Position = ProjectMatrix * gl_Position;
v_texcoord = a_texcoord;
v_normal = mat3(IT_ModelMatrix) * a_normal;
v_tangent = mat3(ModelMatrix) * a_tangent;
}
(2) 片元著色器
我們首先讀取法線,然後將法線進行空間的轉換,再像平時一樣做光照計算。其中,為了保證T一定垂直於N,需要在片元著色器中做一次矯正。然後通過叉乘得到B,以獲取TBN矩陣。
uniform sampler2D brick_N;
uniform sampler2D brick_D;
uniform vec3 LightLocation;
uniform vec3 cameraPos;
varying vec3 worldPos;
varying vec3 v_tangent;
varying vec3 v_normal;
varying vec2 v_texcoord;
vec3 UnpackNormal(vec3 normal)
{
vec3 N = normalize(v_normal);
vec3 T = normalize(v_tangent - N * v_tangent * N);
vec3 B = cross(N, T);
mat3 TBN = mat3(T,B,N);
normal = normalize(2 * normal - 1);
normal = normalize(TBN * normal);
return normal;
}
void main()
{
vec3 normal = texture2D(brick_N, v_texcoord);
normal = UnpackNormal(normal);
vec3 lightDir = normalize(LightLocation - worldPos);
vec3 ViewDir = normalize(cameraPos - worldPos);
float diffuse = 0.7 * clamp(dot(normal, lightDir), 0, 1);
float ambient = 0.2;
vec3 reflectDir = normalize(reflect(-lightDir,normal));
float specular = pow(clamp(dot(reflectDir,ViewDir),0,1),5.0);
vec3 color = texture2D(brick_D, v_texcoord);
vec3 finalColor = color * ( specular +diffuse + ambient);
gl_FragColor = vec4(finalColor, 1);
}
