CUDA 六 從並行排序方法理解並行化思維——冒泡 歸併 雙調排序的GPU實現
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow
也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
在第五講中我們學習了GPU三個重要的基礎並行演算法: Reduce, Scan 和 Histogram,分析了 其作用與串並行實現方法。 在第六講中,本文以氣泡排序 Bubble Sort、歸併排序 Merge Sort 和排序網路中的雙調排序 Bitonic Sort
在並行方法中,我們將考慮到並行方法需要注意的特點進行設計,希望大家在讀完本文後對GPU上並行演算法的設計有一些粗淺的認識。需注意的特點如下:
1. 充分發揮硬體能力(儘量不要有空閒且一直處於等待狀態的SM)
2. 限制branch divergence(見CUDA系列學習(二))
3. 儘量保證記憶體集中訪問(即防止不命中)
( 而我們在資料結構課上學習的sort演算法往往不注意這幾點。)
CUDA系列學習目錄:
CUDA系列學習(一)An Introduction to GPU and CUDA
CUDA系列學習(二)CUDA memory & variables - different memory and variable types
CUDA系列學習(三)GPU設計與結構QA & coding練習
CUDA系列學習(四)Parallel Task型別 與 Memory Allocation
CUDA系列學習(五)GPU基礎演算法: Reduce, Scan, Histogram
I. Bubble Sort
氣泡排序,相信大家再熟悉不過了。經典氣泡排序通過n輪有序冒泡(n為待排序的陣列長度)得到有序序列, 其空間複雜度O(1), 時間複雜度O(n^2)。
那麼如何將氣泡排序演算法改成並行演算法呢? 這裡就需要解除一些依賴關係, 比如是否能解除n輪冒泡間的序列依賴 & 是否能解除每一輪冒泡內部的序列依賴, 使得同樣的n^2次冒泡操作可以通過並行, 降低step complexity。
1996年, J Kornerup針對這些問題提出了odd-even sort演算法,並在論文中證明了其排序正確性。
I.1 從Bubble Sort到Odd-even Sort
先來看一下odd-even sort的排序方法:

圖1.1
上圖為odd-even sort的基本方法。
奇數步中, array中奇數項array[i]與右邊的item(array[i + 1])比較;
偶數步中, array中奇數項array[i]與左邊的item(array[i - 1]) 比較;
這樣,同一個step中的各個相鄰比較就可以並行化了。
PS: 對於array中有偶數個元素的陣列也是一樣:
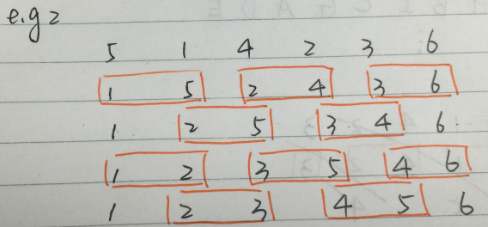
圖1.2
I.2 Odd-even Sort複雜度
在odd-even sort的演算法下, 原本O(n^2)的總比較次數不變,但是由於並行,時間複雜度降到O(n), 即
step complexity = O(n)
work complexity = O(n^2)
code詳見 < Bubble sort and its variants >
II. Merge Sort
看過odd-even sort後,我們來看如何將歸併排序並行化。資料結構課上我們都學過經典歸併排序: 基於divide & conquer 思想, 每次將一個array分拆成兩部分, 分別排序後合併兩個有序序列。 可以通過 T(n)=2T(n/2)+n 得到, 其complexity = O(nlogn)。 和I.1節類似, 我們看看merge sort中的哪些步是可以並行的。
這裡可以將基於merge sort的大規模資料排序分為三部分。 經過divide步之後, 資料分佈如圖所示:
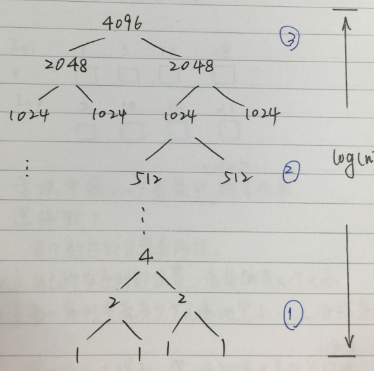
圖2.1
最下端的為 大量-短序列 的合併;
中間一塊為中等數量-中等長度序列 的合併;
最上端的為少量-長序列 的合併;
我們分這三部分進行並行化。 之後大家會明白為啥要這麼分~
II.1 Step 1: Huge number of small tasks
這一部分,每一部分序列合併的代價很小, 而有眾多這樣的任務。 所以我們採取給每個merge一個thread去執行, thread 內部就用序列merge的方法。
II.2 Step 2: Mid number of mid task
在這一階段, 有中等數量的task, 每個task的工作量也有一定增長。 所以我們採取給每個merge一個SM去執行, 每個block上執行的多個thread並行merge的方法。 和step1中的主要區別就是block內部merge從序列改成了並行。 那麼怎樣去做呢?
如下圖所示,假如現在有兩個長為4個元素的array, 想對其進行排序, 將merge排序結果index 0 - 7 寫入資料下方方塊。
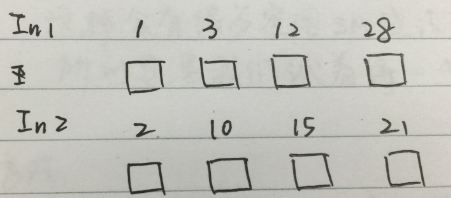
圖2.2
做法:
對於array中的每個數字, 看兩個位置:
1. 自己所在序列的位置: 看它前面有幾個元素
2. 另一個序列的位置: 另一個序列中有多少個元素比它小(採用二分搜尋)
這樣做來, 第一步O(1)可得到, 第二步二分查詢O(logn)可得到; 整個merge過程用shared memory存結果。
II.3 Step 3: Small number of huge task
第三個環節中,也就是merge的頂端(最後一部分),每個merge任務的元素很多, 但是merge任務數很少。 這種情況下, 如果採用Step2的方法, 最壞的情況就是隻有一個很大的task在跑, 此時只有1個SM在忙, 其他空閒SM卻沒法利用, 所以這裡我們嘗試將一個任務分給多個SM執行。
方法: 如圖2.3所示, 將每個序列以256個元素為單位分段, 得到兩個待merge序列In1和In2。然後,對這些端節點排序,如EABFCGDH。 如step2中的方法, 我們計算每個段節點在另一個短序列(長256)中的位置, 然後只對中間那些不確定的部分進行merge排序, 每個merge分配一個SM。
如E~A的部分,
1. 計算出E在In1中的位置posE1, A在In2中的位置posA2
2. merge In1中 posE1~A 和 In2中 E~posA2的元素
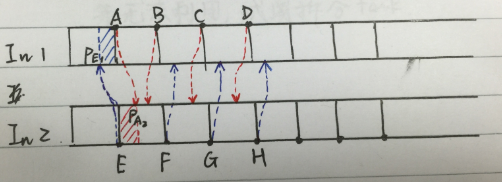
圖2.3
II.4 Merge sort in GPU
以上面step 1的merge sort為例, 其gpu程式碼中kernel函式如下:
其中temp為排好序的序列, 每次排序兩個大小為sortedsize的block,為temp賦值2 * sortedsize個元素。
所以實際上,sortedsize就是一個sorted block的大小。
__global__ void mergeBlocks(int *a, int *temp, int sortedsize){ int id = blockIdx.x; int index1 = id * 2 * sortedsize; int endIndex1 = index1 + sortedsize; int index2 = endIndex1; int endIndex2 = index2 + sortedsize; int targetIndex = id * 2 * sortedsize; int done = 0; while (!done) { if ((index1 == endIndex1) && (index2 < endIndex2)) temp[targetIndex++] = a[index2++]; else if ((index2 == endIndex2) && (index1 < endIndex1)) temp[targetIndex++] = a[index1++]; else if (a[index1] < a[index2]) temp[targetIndex++] = a[index1++]; else temp[targetIndex++] = a[index2++]; if ((index1 == endIndex1) && (index2 == endIndex2)) done = 1; }}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
主函式中,定義block大小並呼叫kernel function:
int blocks = BLOCKS/2; int sortedsize = THREADS; while (blocks > 0) { mergeBlocks<<<blocks,1>>>(dev_a, dev_temp, sortedsize); cudaMemcpy(dev_a, dev_temp, N*sizeof(int), cudaMemcpyDeviceToDevice); blocks /= 2; sortedsize *= 2; } cudaMemcpy(a, dev_a, N*sizeof(int), cudaMemcpyDeviceToHost);
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
III. Bitonic Sort
III.1 Bitonic Sequence 雙調序列
不同於以上兩種排序方法, 現在我們要接觸的 雙調排序 是排序網路方法中的一種。 想起當年在浙大面試某導師的實驗室時就是讓實現的雙調排序, 並不斷優化, 不過當時土得一坨, 就沒聽說過這個演算法。。。 最後寫出個多執行緒就結束了, 後來也沒再整理。 現在我們來看看bitonic sort是個什麼鬼。
雙調排序是排序網路中最快的方法之一。所謂的排序網路是data-independent的排序, 即網路比較順序與資料無關的排序方法, 所以特別適合硬體做並行化。
在瞭解雙調排序演算法之前,我們先來看看什麼是雙調序列。 雙調序列是一個先單調遞增後單調遞減 或者 先單調遞減後單調遞增的序列。
III.2 雙調排序演算法
假如我們現在拿到了雙調序列, 怎樣對它按照從小到大進行排序呢?形象一點來看, 我們將一個雙調序列切成兩半, 每一段的單調性統一, 然後如下圖圖3.1所示, 將兩段疊放起來, 進行兩兩比較, 這樣一定能夠在左右兩段分別得到一個雙調序列(想想為什麼得到的是兩個雙調序列), 且左邊的雙調序列中元素全部小於右側得到的雙調序列的所有元素。 迭代這個過程, 每次都能將序列二分成兩個子雙調序列, 直到這個子雙調序列的長度為2, 也就變成了一個單調子序列, 這個過程排序後原先的長雙調序列就變為有序了 。 整個過程如下圖圖3.2所示。
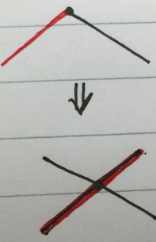
圖3.1
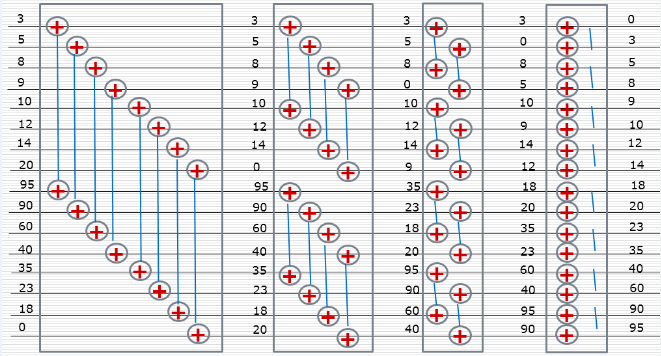
圖3.2
III.3 任意序列生成雙調序列
好,III.2中講了怎樣對雙調序列進行排序, 那問題來了,怎樣從任意序列生成雙調序列呢? 這裡可以看看本文最後的參考文獻3, 寫得很詳細。 這個過程叫Bitonic merge, 實際上也是divide and conquer的思路。 和III.2中的思路正相反, 我們可以將兩個相鄰的,單調性相反的單調序列看作一個雙調序列, 每次將這兩個相鄰的,單調性相反的單調序列merge生成一個新的雙調序列, 然後排序(同III.2)。 這樣只要每次兩個相鄰長度為n的序列的單調性相反, 就可以通過連線得到一個長度為2n的雙調序列。 n開始為1, 每次翻倍,直到等於陣列長度, 就只需要一遍單方向(單調性)排序了。
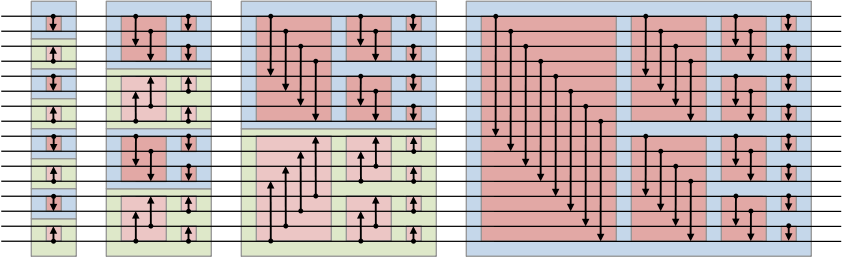
圖3.3
以16個元素的array為例,
1. 相鄰兩個元素合併形成8個單調性相反的單調序列,
2. 兩兩序列合併,形成4個雙調序列,分別按相反單調性排序
3. 4個長度為4的相反單調性單調序列,相鄰兩個合併,生成兩個長度為8的雙調序列,分別排序
4. 2個長度為8的相反單調性單調序列,相鄰兩個合併,生成1個長度為16的雙調序列,排序
總算講完了,那麼腫麼實現呢? 我們看這個過程需要控制哪些地方? 如上圖所示, 我們可以將len=16的array的雙調排序分成4部分,每一部分結束都會形成若干長度為 i 的單調序列。 在每一部分中,用 j 表示比較的間隔,如下圖所示每一時刻的i和j。
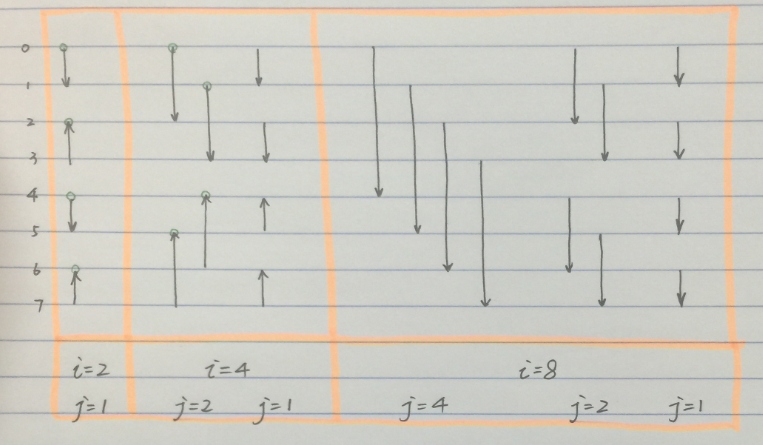
圖3.4
III.4 雙調排序的並行實現
本著“talk is cheap, show me the code”的優良作風, 拿粗來雙調排序的GPU實現程式碼share如下:
/* * Author: Rachel * <[email protected]> * * File: bitonic_sort.cu * Create Date: 2015-08-05 17:10:44 * */#include<iostream>#include<stdio.h>#include<stdlib.h>#include"gputimer.h"#include<time.h>#define NThreads 8#define NBlocks 4#define Num NThreads*NBlocksusing namespace Gadgetron;__device__ void swap(int &a, int &b){ int t = a; a = b; b = t;}__global__ void bitonic_sort(int* arr){ extern __shared__ int shared_arr[]; const unsigned int tid = blockIdx.x * blockDim.x + threadIdx.x; //const unsigned int tid = threadIdx.x; shared_arr[tid] = arr[tid]; __syncthreads(); //for(int i=2; i<=blociDim.x; i<<=1){ for(unsigned int i=2; i<=Num; i<<=1){ for(unsigned int j=i>>1; j>0; j>>=1){ unsigned int tid_comp = tid ^ j; if(tid_comp > tid){ if((tid & i)==0){ //ascending if(shared_arr[tid]>shared_arr[tid_comp]){ swap(shared_arr[tid],shared_arr[tid_comp]); } } else{ //desending if(shared_arr[tid]<shared_arr[tid_comp]){ swap(shared_arr[tid],shared_arr[tid_comp]); } } } __syncthreads(); } } arr[tid] = shared_arr[tid];}int main(int argc, char* argv[]){ GPUTimer timer; int* arr= (int*) malloc(Num*sizeof(int)); //init array value time_t t; srand((unsigned)time(&t)); for(int i=0;i<Num;i++){ arr[i] = rand() % 1000; } //init device variable int* ptr; cudaMalloc((void**)&ptr,Num*sizeof(int)); cudaMemcpy(ptr,arr,Num*sizeof(int),cudaMemcpyHostToDevice); for(int i=0;i<Num;i++){ printf("%d\t",arr[i]); } printf("\n"); dim3 blocks(NBlocks,1); dim3 threads(NThreads,1); timer.start(); bitonic_sort<<<blocks,threads,Num*sizeof(int)>>>(ptr); //bitonic_sort<<<1,Num,Num*sizeof(int)>>>(ptr); timer.stop(); cudaMemcpy(arr,ptr,Num*sizeof(int),cudaMemcpyDeviceToHost); for(int i=0;i<Num;i++){ printf("%d\t",arr[i]); } printf("\n"); cudaFree(ptr); return 0;}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
code中,
tid^j用於單方向判斷, 防止同一元素比較兩次;
tid & i == 0 用於判斷這個部分應該是單增還是單減, 因為方向在每個長為i的單調序列中是一致的, 所以選用i判斷單調方向。
參考文獻:
1. Bubble sort and its variants
2. nvidia的mergesort實現
3. 我用過的淺顯易懂的Bitonic sort文件
歡迎大家交流
給我老師的人工智慧教程打call!http://blog.csdn.net/jiangjunshow

