（一） 複雜度分析的由來

     我們平時寫程式碼的時候，想要知道一段程式碼的執行時間，佔用空間等等，一般都是在程式碼開始的記錄一下當前時間，執行結束的時候，再記錄一下時間，最後得出這段程式碼的執行時間，一般就是通過這個來判斷我們的程式碼的執行效率。這種做法沒有錯，但是這樣做統計出來的。

      在我之前寫業務程式碼的時候，比如增刪查改的時候，我經常都是這麼幹的，為了讓一個查詢更快，更有效率，邊除錯，邊分析，找出慢的步驟，再逐一解決。那麼問題來了，我們還需要學這個演算法的時間複雜度分析嗎？

      對於這個問題，之前我也是很茫然，看到演算法時間複雜度分析的相關內容，我就直接忽略，想著工作中也不會這麼分析。

      那麼，我先解釋一下，上面這種做法有什麼弊端呢（其實上面的做法，真心還行）。 1、我們通過這種程式碼得出來的執行時間是很依靠機器的硬體的，要看你CPU的計算能力，記憶體的大小等等（不是很多時候，都會有這麼一個情況，線下測試很快，線上慢成狗了，因為沒有考慮到CPU的分配情況，記憶體佔用情況）。2、這種統計方法受到資料規模的影響很大，在測試環境，測得再OK，上線之後還是問題很大）。

     基於上面這些問題，IT的大牛們，就想了一下，要不對演算法的時間複雜度來個抽象，不要依賴於機器，硬體等等做法呢。所以他們就提出了一種做法就做O(n)，時間複雜度做法。

 （二）什麼是時間複雜度O(n）

      時間複雜度：它並不是表示程式碼的真正執行時間，而是表示程式碼的執行時間隨資料規模增長的變化情況。

      下面來看這個例子。

    int GetSum(int n)
    {
    1       var sum = 0;
    2       for (var i = 0; i < n; i++)
            {
    3             sum += i;
            }
            return sum;
   }
 

         我們知道每個語句的執行操作，從CPU的角度來看，就是讀資料--運算--寫資料，假設這整個操作需要一個單位的時間。我們假設一行程式碼就是一個單位的執行時間，那麼這段程式碼就是2+2n個單位時間，從這裡可以看出來程式的執行時間是和n成正比的。我們把這個規律總結成為一個公式，就是我們的時間複雜度。

    （三）時間複雜度的分析方法

          1、關注執行次數最多的那段程式碼，那個就是這整段程式碼的時間複雜度

          2、乘法法則，兩個時間複雜度相乘，就是整個時間複雜度。（巢狀內外程式碼的複雜度等於內外複雜度的乘積）

          3、總的複雜度等於最大的那個複雜度。（一般兩個複雜度，不是同一個層級的時候，才取最大的，比如o(n)和o(n2),則取o(n2)，如果一個是o(n),另外一個是o(m),則時間複雜度就是o(m+n)）

      (四）總結

           感覺這個時間複雜度分析，就像設計模式，你說按照設計模式寫出來的程式碼，也不一定是最好的。我們時間複雜度也是一樣，也不一定說o(n)就比o(n2)的好，但是隻要當我們一提到某某某設計模式的時候，心裡馬上就可以勾勒出這個設計模式的程式碼組成結構。當我們一說o(n)的時候，也可以知道這段程式碼是如何組織的。

          還有很多常見的時間複雜度，比如o(1),o(n) o(logn) o(nlogn),o(n2)。下面說說我覺得最難分析的o(logn)這個時間複雜度把。

  int GetSum(int n)
  {
            var i = 1;
            while (i<=n)
            {
                i = i*2;
            }
            return i;
  }

        上面這個例子，一步步來分析，i=2,I=4,i=8,i=16,一直到i<=n。  那這個程式碼執行了多次呢。就是2的x次方小於等於n。 現在要求這個x是多少呢，那就用到我們的對數了x=log2為底，n為真數的對數了。

     int GetSum(int n)
        {
            var i = 1;
            while (i<=n)
            {
                i = i*3;
            }
            return i;
        }

        這個例子也是和上面是一樣的，它是Log3為底,n為真數的對數。

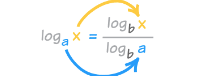
        我們知道對數是可以相互轉化的了 。對數都是可以相互轉化的，我們同時把他們轉化為以十為底的對數，然後去掉常量，就得到了o(logn)。然後o(nlogn)就是n個o(logn)相乘。