關於RBF神經網路的學習總結
在這裡總結下科研需要用到的RBF神經網路知識。
https://www.cnblogs.com/pinking/p/9349695.html
https://blog.csdn.net/guoyunlei/article/details/74529320
https://www.cnblogs.com/pinking/p/9349695.html
https://wenku.baidu.com/view/c61384dda58da0116c174946.html
RBF神經網路
RBF神將網路是一種三層神經網路,其包括輸入層、隱層、輸出層。從輸入空間到隱層空間的變換是非線性的,而從隱層空間到輸出層空間變換是線性的。流圖如下:

RBF基本思想
RBF網路的基本思想是:用RBF作為隱單元的“基”構成隱含層空間,這樣就可以將輸入向量直接對映到隱空間,這個對映的過程就通過RBF函式完成(下面介紹RBF即徑向基函式)而不需要通過權連線。當RBF的中心點確定以後,這種對映關係也就確定了。而隱含層空間到輸出空間的對映是線性的,即網路的輸出是隱單元輸出的線性加權和,此處的權即為網路可調引數。
其中,隱含層的作用是把向量從低維度的p對映到高維度的h,這樣低維度線性不可分的情況到高維度就可以變得線性可分了,主要就是核函式的思想。
這樣,網路由輸入到輸出的對映是非線性的,而網路輸出對可調引數而言卻又是線性的。網路的權就可由線性方程組直接解出,從而大大加快學習速度並避免區域性極小問題。
RBF函式:
徑向基函式是一個取值僅僅依賴於離原點距離的實值函式,也就是Φ(x)=Φ(‖x‖),或者還可以是到任意一點c的距離,c點稱為中心點,也就是Φ(x,c)=Φ(‖x-c‖)。任意一個滿足Φ(x)=Φ(‖x‖)特性的函式Φ都叫做徑向基函式,標準的一般使用歐氏距離(也叫做歐式徑向基函式),儘管其他距離函式也是可以的。最常用的徑向基函式是高斯核函式 ,形式為 k(||x-xc||)=exp{- ||x-xc||2/(2*σ)2) } 其中x_c為核函式中心,σ為函式的寬度引數 , 控制了函式的徑向作用範圍。
函式表示
徑向基神經網路的啟用函式可表示為:
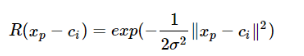
其中xp徑向基神經網路的結構可得到網路的輸出為:
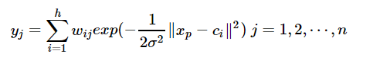
當然,採用最小二乘的損失函式表示:
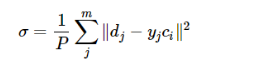
梯度下降
簡單易懂的推導:
https://blog.csdn.net/pengchengliu/article/details/80932232
